1.9. Поиск всех деревьев на графе.
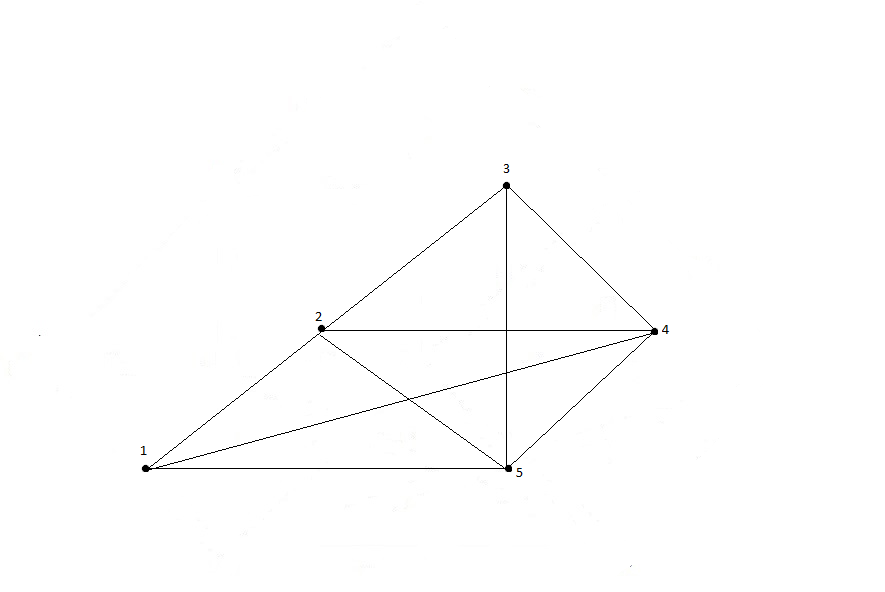Рис.
1.17
– Исходный граф для поиска всех деревьев.
Определим количество деревьев с помощью матрицы Кирхгофа и алгоритма Трента. Матрица (по диагонали степени вершин, элементы – число путей со знаком «-»).
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
3 |
-1 |
0 |
-1 |
-1 |
|
2 |
-1 |
4 |
-1 |
-1 |
-1 |
A = |
3 |
0 |
-1 |
3 |
-1 |
-1 |
|
4 |
-1 |
-1 |
-1 |
4 |
-1 |
|
5 |
-1 |
-1 |
-1 |
-1 |
4 |
|
|
|
|
|
|
|
По алгоритму выбираем один из главных миноров (вычеркиваем строку и столбец, соответствующие элементу главной диагонали). Например, 1 и 1 – в данном случае это полностью безразлично, граф полносвязный без кратных ребер.
|
4 |
-1 |
-1 |
-1 |
11 = |
-1 |
3 |
-1 |
-1 |
|
-1 |
-1 |
4 |
-1 |
|
-1 |
-1 |
-1 |
4 |
0 |
11 |
-5 |
-5 |
|
|
|
|
|
|
|
-1 |
3 |
-1 |
-1 |
|
|
|
1 |
-5 |
- |
+(3) |
0 |
-4 |
5 |
0 |
= |
(-1) |
(-1)1+2 |
-4 |
5 |
0 |
= |
0 |
-4 |
0 |
5 |
|
|
|
-4 |
0 |
5 |
|
1
5
4(2)
=
-(2)
-(2)
7 |
-5 |
-4 |
5 |
= 5* = 5*(35 – 20) = 75.
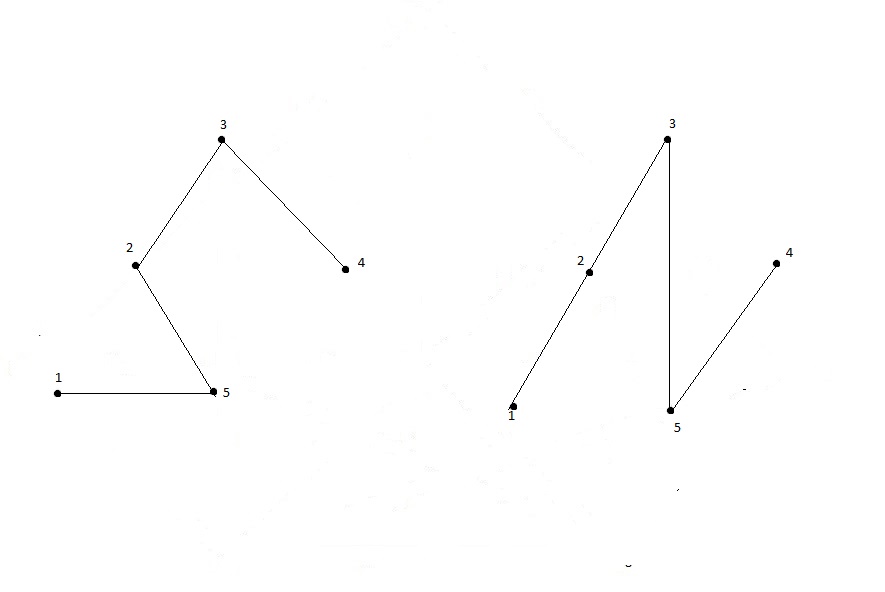
Итого, мы ожидаем получить 75 деревьев.
Рис. 1.18 Примеры деревьев.
2. Постановка задачи на программирование