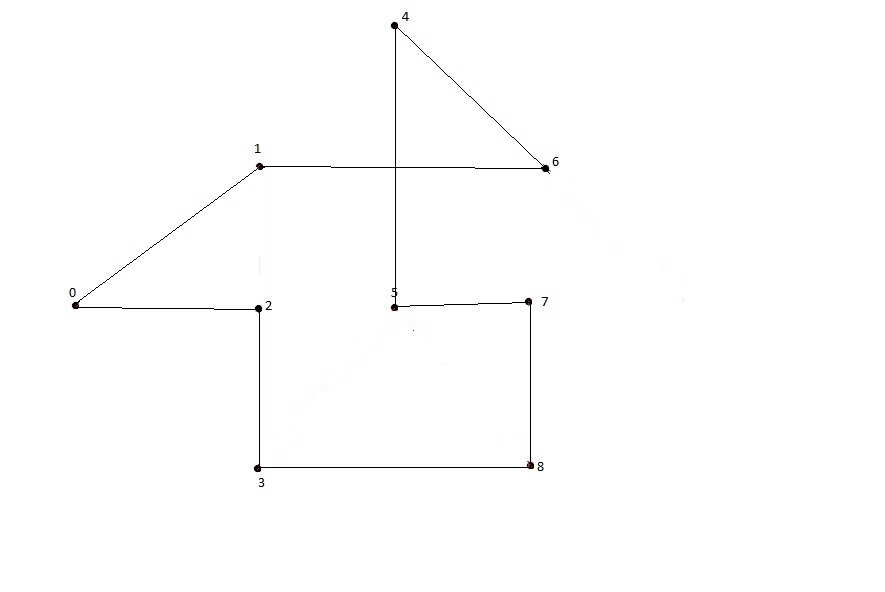
1.8 Задача коммивояжера
Решение задачи коммивояжера методом Литтла
Получим матрицу стоимости для нашего графа, элементами которой являются веса соответствующих дуг. Все элементы по диагонали матрицы приравниваем к бесконечности
∞ |
2 |
3 |
5 |
∞ |
∞ |
∞ |
∞ |
∞ |
2 |
∞ |
1 |
∞ |
∞ |
∞ |
4 |
∞ |
∞ |
3 |
1 |
∞ |
1 |
∞ |
5 |
∞ |
∞ |
5 |
5 |
∞ |
1 |
∞ |
∞ |
1 |
∞ |
∞ |
2 |
∞ |
∞ |
∞ |
∞ |
∞ |
10 |
2 |
∞ |
∞ |
∞ |
∞ |
5 |
1 |
10 |
∞ |
5 |
6 |
1 |
∞ |
4 |
∞ |
∞ |
2 |
5 |
∞ |
11 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
6 |
11 |
∞ |
1 |
∞ |
∞ |
5 |
2 |
∞ |
1 |
∞ |
1 |
∞ |
Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
0 |
∞ |
0 |
1 |
3 |
∞ |
∞ |
∞ |
∞ |
∞ |
1 |
1 |
∞ |
0 |
∞ |
∞ |
∞ |
3 |
∞ |
∞ |
2 |
2 |
0 |
∞ |
0 |
∞ |
4 |
∞ |
∞ |
4 |
3 |
4 |
∞ |
0 |
∞ |
∞ |
0 |
∞ |
∞ |
1 |
4 |
∞ |
∞ |
∞ |
∞ |
∞ |
8 |
0 |
∞ |
∞ |
5 |
∞ |
∞ |
4 |
0 |
9 |
∞ |
4 |
5 |
0 |
6 |
∞ |
2 |
∞ |
∞ |
0 |
3 |
∞ |
9 |
∞ |
7 |
∞ |
∞ |
∞ |
∞ |
∞ |
5 |
10 |
∞ |
0 |
8 |
∞ |
∞ |
4 |
1 |
∞ |
0 |
∞ |
0 |
∞ |
То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
0 |
∞ |
0 |
1 |
3 |
∞ |
∞ |
∞ |
∞ |
∞ |
1 |
0 |
∞ |
0 |
∞ |
∞ |
∞ |
3 |
∞ |
∞ |
2 |
1 |
0 |
∞ |
0 |
∞ |
4 |
∞ |
∞ |
4 |
3 |
3 |
∞ |
0 |
∞ |
∞ |
0 |
∞ |
∞ |
1 |
4 |
∞ |
∞ |
∞ |
∞ |
∞ |
8 |
0 |
∞ |
∞ |
5 |
∞ |
∞ |
4 |
0 |
9 |
∞ |
4 |
5 |
0 |
6 |
∞ |
2 |
∞ |
∞ |
0 |
3 |
∞ |
9 |
∞ |
7 |
∞ |
∞ |
∞ |
∞ |
∞ |
5 |
10 |
∞ |
0 |
8 |
∞ |
∞ |
4 |
1 |
∞ |
0 |
∞ |
0 |
∞ |
Текущая Нижняя граница=13у.е.
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца. Г0,1=1, Г1,0=1, Г1,2=0, Г2,1=0, Г2,3=0, Г3,2=0, Г3,5=0, Г4,6=8, Г5,3=0, Г5,9=0, Г6,4=9, Г7,8=5, Г8,7=5, Г8,5=0. Максимальное значение имеет Г6,4=9 Удалим из матрицы стоимости строку 6 и столбец 4. Внесем в текущий ориентированный граф дугу (6,4). Присвоим элементу (4,6) значение бесконечности, чтобы избежать преждевременного замыкания контура.
|
0 |
1 |
2 |
3 |
5 |
6 |
7 |
8 |
0 |
∞ |
0 |
1 |
3 |
∞ |
∞ |
∞ |
∞ |
1 |
0 |
∞ |
0 |
∞ |
∞ |
3 |
∞ |
∞ |
2 |
1 |
0 |
∞ |
0 |
4 |
∞ |
∞ |
4 |
3 |
3 |
∞ |
0 |
∞ |
0 |
∞ |
∞ |
1 |
4 |
∞ |
∞ |
∞ |
∞ |
8 |
∞ |
∞ |
∞ |
5 |
∞ |
∞ |
4 |
0 |
∞ |
4 |
5 |
0 |
7 |
∞ |
∞ |
∞ |
∞ |
5 |
10 |
∞ |
0 |
8 |
∞ |
∞ |
4 |
1 |
0 |
∞ |
0 |
∞ |
То же проделаем. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
|
0 |
1 |
2 |
3 |
5 |
6 |
7 |
8 |
0 |
∞ |
0 |
1 |
3 |
∞ |
∞ |
∞ |
∞ |
1 |
0 |
∞ |
0 |
∞ |
∞ |
0 |
∞ |
∞ |
2 |
1 |
0 |
∞ |
0 |
4 |
∞ |
∞ |
4 |
3 |
3 |
∞ |
0 |
∞ |
0 |
∞ |
∞ |
1 |
4 |
∞ |
∞ |
∞ |
∞ |
0 |
∞ |
∞ |
∞ |
5 |
∞ |
∞ |
4 |
0 |
∞ |
1 |
5 |
0 |
7 |
∞ |
∞ |
∞ |
∞ |
5 |
7 |
∞ |
0 |
8 |
∞ |
∞ |
4 |
1 |
0 |
∞ |
0 |
∞ |
Текущая Нижняя граница=24у.е. Максимальное значение имеет Г4,5=∞. Удалим из матрицы стоимости строку 4 и столбец 5. Внесем в текущий ориентированный граф дугу (4,5). Присвоим элементу (5,6) значение бесконечности, чтобы избежать преждевременного замыкания контура.
Каждая трока и каждый столбец содержит ноль.
|
0 |
1 |
2 |
3 |
6 |
7 |
8 |
0 |
∞ |
0 |
1 |
3 |
∞ |
∞ |
∞ |
1 |
0 |
∞ |
0 |
∞ |
0 |
∞ |
∞ |
2 |
1 |
0 |
∞ |
0 |
∞ |
∞ |
4 |
3 |
3 |
∞ |
0 |
∞ |
∞ |
∞ |
1 |
5 |
∞ |
∞ |
4 |
0 |
∞ |
5 |
0 |
7 |
∞ |
∞ |
∞ |
∞ |
7 |
∞ |
0 |
8 |
∞ |
∞ |
4 |
1 |
∞ |
0 |
∞ |
Максимальное значение имеет Г7,8=7 Удалим из матрицы стоимости строку 7 и столбец 8. Внесем в текущий ориентированный граф дугу (7,8). Присвоим элементу (8,7) значение бесконечности, чтобы избежать преждевременного замыкания контура.
|
0 |
1 |
2 |
3 |
6 |
7 |
0 |
∞ |
0 |
1 |
3 |
∞ |
∞ |
1 |
0 |
∞ |
0 |
∞ |
0 |
∞ |
2 |
1 |
0 |
∞ |
0 |
∞ |
∞ |
3 |
3 |
∞ |
0 |
∞ |
∞ |
∞ |
5 |
∞ |
∞ |
4 |
0 |
∞ |
5 |
8 |
∞ |
∞ |
4 |
1 |
∞ |
∞ |
То же проделаем. Получим матрицу, содержащую нули в каждой строке и каждом столбце.
|
0 |
1 |
2 |
3 |
6 |
7 |
0 |
∞ |
0 |
1 |
3 |
∞ |
∞ |
1 |
0 |
∞ |
0 |
∞ |
0 |
∞ |
2 |
1 |
0 |
∞ |
0 |
∞ |
∞ |
3 |
3 |
∞ |
0 |
∞ |
∞ |
∞ |
5 |
∞ |
∞ |
4 |
0 |
∞ |
0 |
8 |
∞ |
∞ |
3 |
0 |
∞ |
∞ |
Текущая Нижняя граница=30у.е.
Максимальное значение имеет Г5,7=∞ Удалим из матрицы стоимости строку 5 и столбец 7. Внесем в текущий ориентированный граф дугу (5,7).
|
0 |
1 |
2 |
3 |
6 |
0 |
∞ |
0 |
1 |
3 |
∞ |
1 |
0 |
∞ |
0 |
∞ |
0 |
2 |
1 |
0 |
∞ |
0 |
∞ |
3 |
3 |
∞ |
0 |
∞ |
∞ |
8 |
∞ |
∞ |
3 |
0 |
∞ |
Максимальное значение имеет Г1,6=∞.
Удалим из матрицы стоимости строку 1 и столбец 6. Внесем в текущий ориентированный граф дугу (1,6).
|
0 |
1 |
2 |
3 |
0 |
∞ |
0 |
1 |
3 |
2 |
1 |
0 |
∞ |
0 |
3 |
3 |
∞ |
0 |
∞ |
8 |
∞ |
∞ |
3 |
0 |
Получим матрицу, содержащую нули в каждой строке и каждом столбце.
Текущая Нижняя граница=31у.е.
|
0 |
1 |
2 |
3 |
0 |
∞ |
0 |
1 |
3 |
2 |
0 |
0 |
∞ |
0 |
3 |
2 |
∞ |
0 |
∞ |
8 |
∞ |
∞ |
3 |
0 |
Максимальное значение имеет Г8,3=3. Удалим из матрицы стоимости строку 8 и столбец 3. Внесем в текущий ориентированный граф дугу (8,3).
|
0 |
1 |
2 |
0 |
∞ |
0 |
1 |
2 |
0 |
0 |
∞ |
3 |
2 |
∞ |
0 |
Максимальное значение имеет Г3,2=3. Удалим из матрицы стоимости строку 3 и столбец 2. Внесем в текущий ориентированный граф дугу (3,2). Присвоим элементу (2,1) значение бесконечности, чтобы избежать преждевременного замыкания контура.
|
0 |
1 |
0 |
∞ |
0 |
2 |
0 |
∞ |
После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы (2,0) и (0,1).
Рис 1.16. Самый выгодный путь, полученный методом Литтла.
