1.5 Проверка ориентированного графа на наличие циклов путем отбрасывания «истоков» и «стоков»
У нас исток вершина V0, ее исходящие дуги X0={(0,1),(0,2),(0,3)}, рис.1.6.
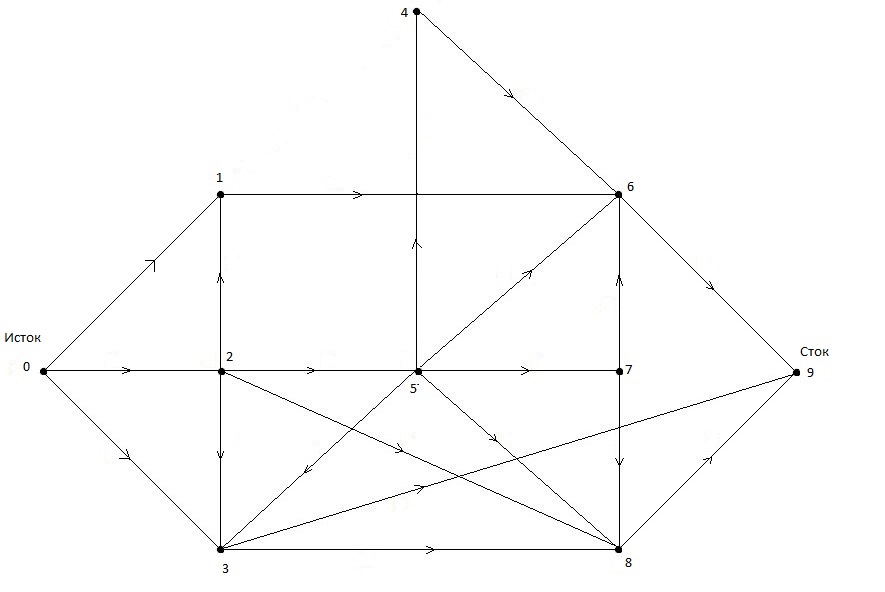
Рисунок 1.6 – Выделение первого истока
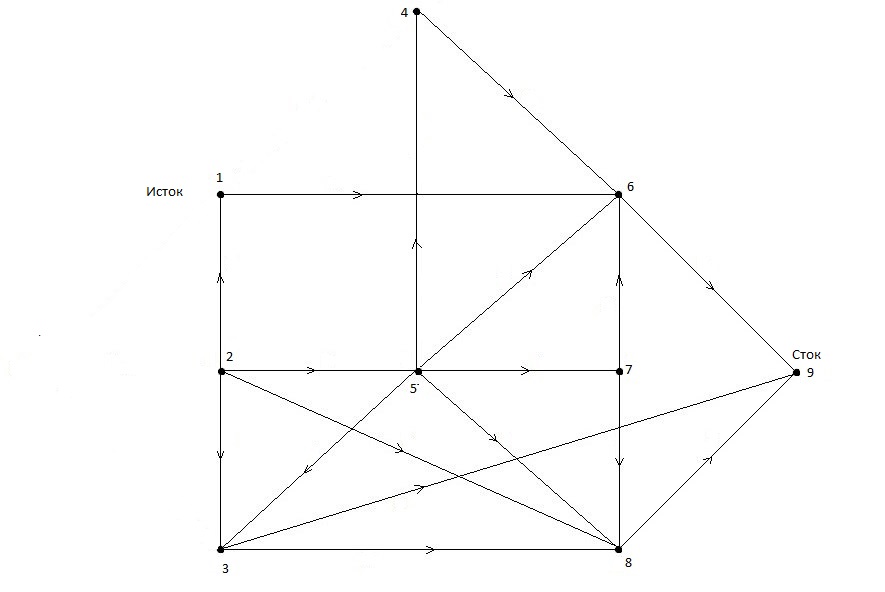
Рисунок 1.7 – Новые истоки после отбрасывания V0
Теперь истоком стала вершина V2, отбрасываем ее и дуги X2={(2,1), (2,3),(2,5),(2,8)}, рис.1.8.
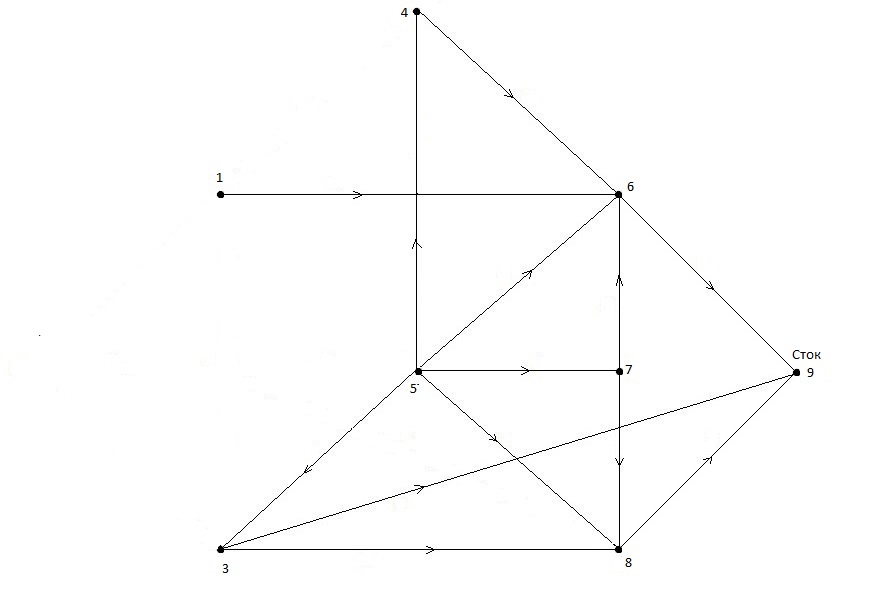
Рисунок 1.8 – Подграф, полученный отбрасыванием вершины V2.
В оставшемся подграфе истоком является вершина V5, отбрасываем ее и дуги X5={(5,4),(5,6),(5,7),(5,8),(5,3)}.
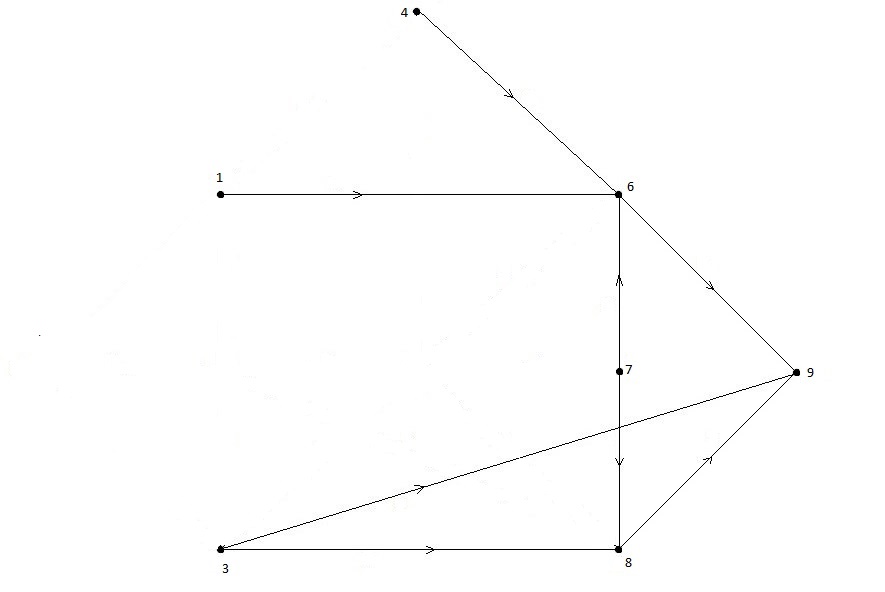
Рисунок 1.9 – Подграф, полученный отбрасыванием вершины V5
В оставшемся подграфе истоком является вершина V3, отбрасываем ее и дуги X3 ={(3,9),(3,8)}, рис.1.10.
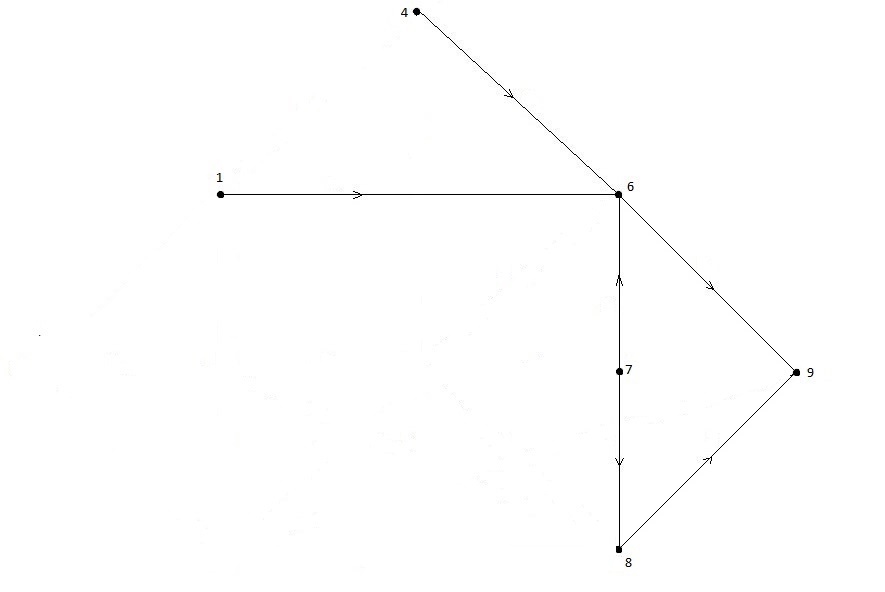
Рисунок 1.10 – Подграф, полученный отбрасыванием вершины V3
В оставшемся подграфе истоком является вершина V7, отбрасываем ее и дуги X7 ={(7,6), (7,8)}, рис.1.11.
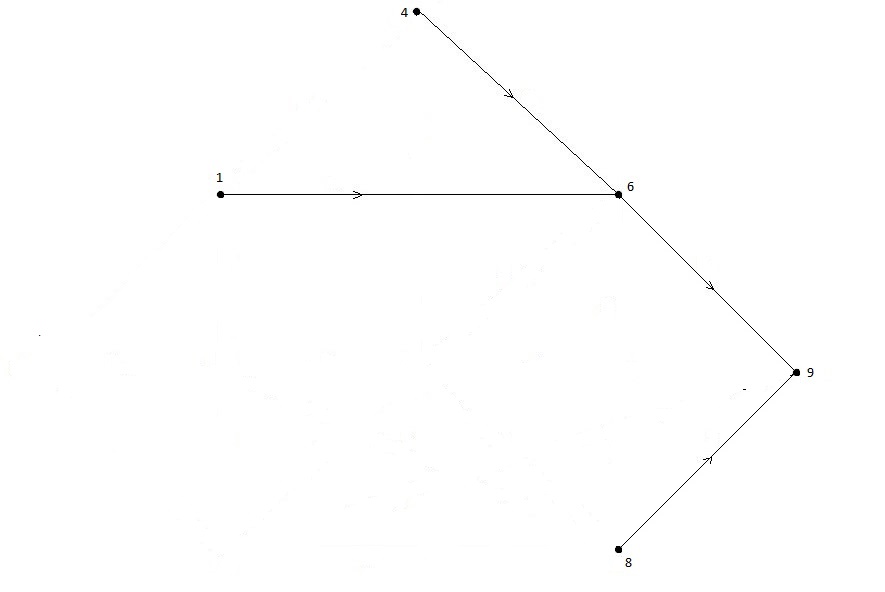
Рисунок 1.11 – Подграф, полученный отбрасыванием вершины V7
В результате у нас остается подграф слабо связный, а следовательно, в результате исследования графа мы доказали, что граф Gор циклов не имеет.
1.6 Поиск основного (остевого) дерева алгоритмом Прима-Краскала
Выписываем таблицу весов ребер, упорядоченную по убыванию, табл.1.2.
Таблица 1.2 Веса ребер графа G
-
Вес
Ребра
1
(2,1), (2,3), (5,3), (5,8), (7,8)
2
(0,1), (3,8), (4,6), (6,9)
3
(0,2)
4
(1,6)
5
(2,5), (2,8), (5,6), (0,3)
6
(5,7),(3,9),(8,9)
10
(5,4)
11
(7,6)
Последовательность шагов по решению задачи Прима-Краскла:
1) выбираем ребро (2,1), окрашиваем вершины V1 и V2 в красный цвет;
2) выбираем ребро (2,3), вершина V2 –красная, V3 пока бесцветная, следовательно, заливаем V3 красным цветом ;
3) следующим выбираем ребро (3,5), вершина V3 красная, V5 - бесцветная, следовательно, заливаем V5 красным цветом;
4) выбираем ребро (5,8), вершина V5 красная, вершина V8 пока бесцветная, закрашиваем V8 в красный цвет;
5) выбираем ребро (7,8), вершина V8 красная, вершина V7 пока бесцветная, закрашиваем V7 в красный цвет;
6) выбираем ребро (0,1), вершина V1 красная, вершина V0 пока бесцветная, закрашиваем V0 в красный цвет;
7) пытаемся выбрать ребро (3,8), но обе его вершины уже красного цвета: это ребро в решение не войдет;
8) выбираем ребро (4,6), обе его вершины бесцветные, следовательно, заливаем V4 и V6 в синий цвет;
9) выбираем ребро (6,9), вершина V6 синяя, вершина V9 пока бесцветная, закрашиваем V9 в синий цвет;
10) пытаемся выбрать ребро (0,2), но обе его вершины уже красного цвета: это ребро в решение не войдет;
11) выбираем ребро (1,6), вершина V1 красная, вершина V6 синяя, следовательно, вершины V6, V4, V9 заливаем красным цветом.
12) мы выбрали 9 ребер на графе из 10 вершин, дерево построено.
Вес найденного дерева - 15. Построенное дерево приведено на рис.1.14.
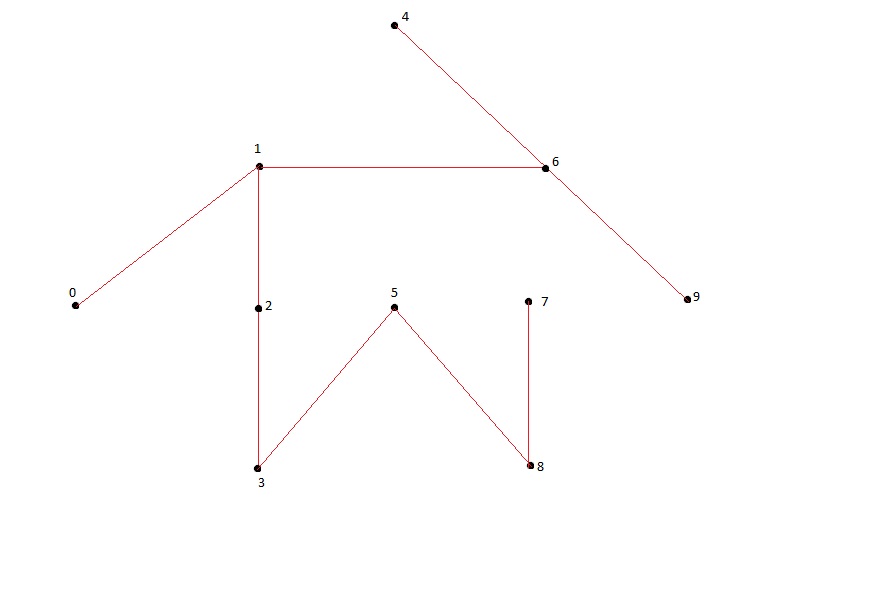
Рисунок 1.14 – Основное дерево, полученное по алгоритму Прима-Краскла
1.7 Определение дерева кратчайших путей по алгоритму Дейкстры
В работе требуется определить кратчайший маршрут от вершины 0 до вершины 9 по алгоритму Дейкстры. В данном параграфе рассматриваем граф как неориентированный (игнорируем направленность дуг, полагая их ребрами).
Достижимость минимальных весов:
q0,1 = 2;
q0,2 = 3;
q0,3 = 4;
q0,5 = 5;
q0,6 = 6;
q0,8 = 6;
q0,7 = 7;
q0,4 = 8;
q0,9 = 8;
Можно продолжать расчеты по алгоритму Дейкстры для вершин 4, 5 и 6, но они уже не повлияют на полученное решение.
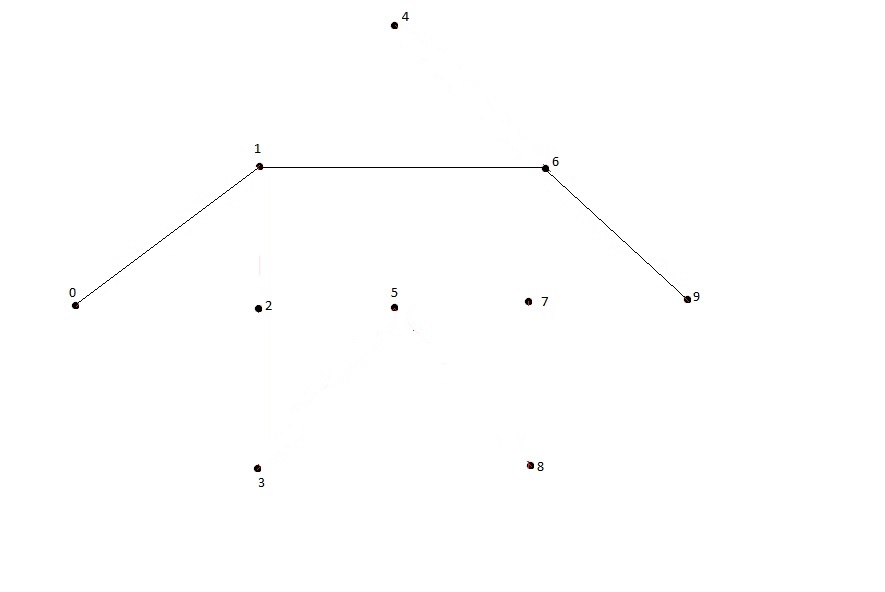
Рис.1.15 Кратчайшие пути, полученные по алгоритму Дейкстры