1.2.6 Степени вершин неориентированного графа:

Степени вершин рассматриваемого неориентированного графа приведены в табл.1.1

Таблица 1.1 Степенная последовательность вершин графа G

Вершины	0	1	2	3	4	5	6	7	8	9
Степени	3	3	5	5	2	6	5	3	5	3

Выбираем из таблицы наибольшую и наименьшую степени:

D_max = 6; D_min = 2.

Примечание. Степенью вершины неориентированного графа называется количество ребер, инцидентных данной вершине.

1.3.2 Нумерация вершин графа g «поисков в глубину»:

Рассмотрим стек нумерации «поиском в глубину». Правило построения LIFO – Last In First Out. Использованы номера вершин исходного графа. Просмотренные вершины выделены жирным шрифтом, уже внесенные в стек вершины заключены в скобки.

Текущая вершина	Стек дополнения	Состояние стека
0	1,2,3	01,2,3
3	8,9	0,1,2,38,9
9	пусто	0,1,2,3,8,9
8	(9)	0,1,2,3,8,9
2	(1),5,(3),(8)	0,1,2,3,8,95
5	(3),4,6,7,(8)	0,1,2,3,8,9,54,6,7
7	(6),(8)	0,1,2,3,8,9,5,4,6,7
6	(9)	0,1,2,3,8,9,5,4,6,7
4	(6)	0,1,2,3,8,9,5,6,4,7
1	(6)	0,1,2,3,8,9,5,4,6,7

Перенумерация:

Старые номера	0	3	9	8	2	5	7	6	4	1
Новые номера	0	1	2	3	4	5	6	7	8	9

Реализация нумерации представлена на рис.1.2. Исходная вершина - .

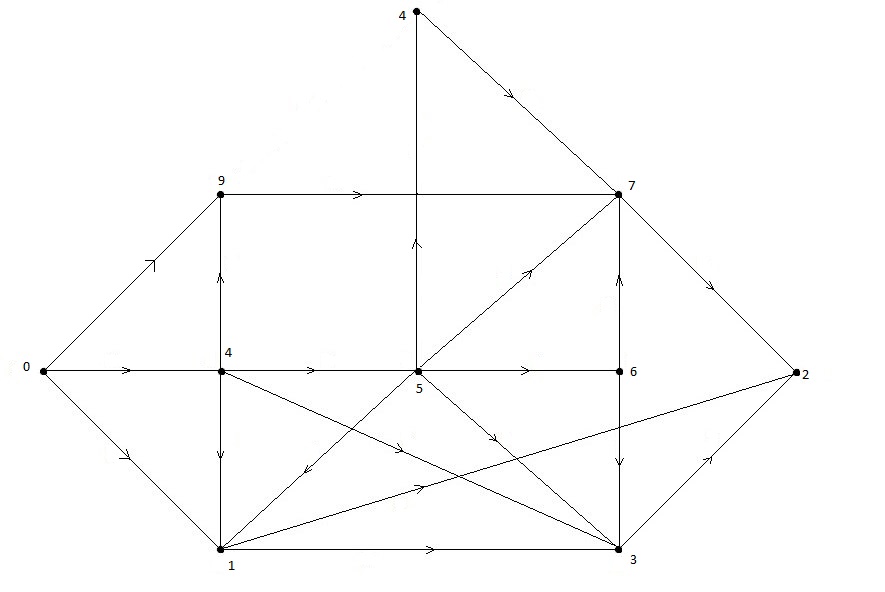
Рисунок 1.2 – Нумерация «поиском в глубину»

1.3.3 Нумерация вершин графа g «поиском в ширину»:

Рассмотрим стек нумерации «поиском в глубину». Правило построения FIFO – First In First Out. Использованы номер а вершин исходного графа. Просмотренные вершины выделены жирным шрифтом, уже внесенные в стек вершины заключены в скобки.

Текущая вершина	Стек дополнения	Состояние стека
0	1,2,3	01,2,3
1	6,	0,1,2,36
2	(1),(3),5,8	0,1,2,3,65,8
3	(8),9	0,1,2,3,6,5,89
6	(9)	0,1,2,3,6,5,8,9
5	4,(6),7,(8),(3)	0,1,2,3,4,6,5,8,94,7
8	(9)	0,1,2,3,6,5,8,9,4,7
9	Пусто	0,1,2,3,6,5,8,9,4,7
4	(6)	0,1,2,3,6,5,8,9,4,7
7	(6),(8)	0,1,2,3,6,5,,8,9,4,7

Перенумерация в данном случае не нужна, поскольку граф уже пронумерован «поиском в ширину», рис.1.3. Исходная вершина - .

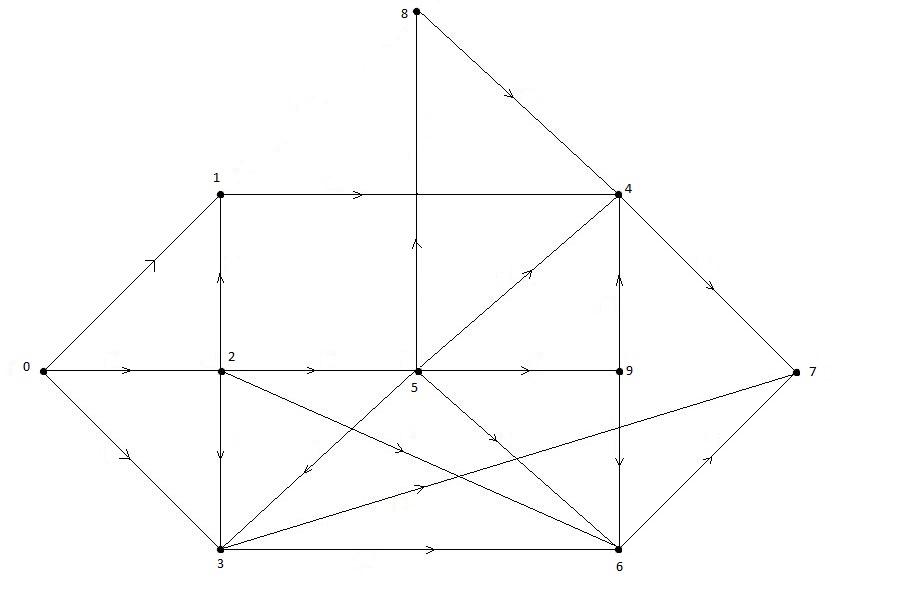
Рисунок 1.3 – Нумерация «поиском в ширину»

1.4 Эйлеров путь и Эйлеров цикл на графе

1.4.1 Для определения Эйлерова путь требуется выписать степенную последовательность вершин графа G и указать в графе G Эйлеров путь. Если такового пути не существует, то в графе G добавить наименьшее число ребер таким образом, чтобы в новом графе можно было указать Эйлерову цепь.

Степенная последовательность вершин графа G:

(3,3,5,5,2,6,5,3,5,3)

Для существования Эйлерова пути допустимо только две вершины с нечетными степенями, поэтому необходимо добавить три ребра, скажем между вершинами 1 и 3, 6 и 8, 7 и 9.

Полученный Эйлеров путь: 0,1,6,4,5,6,8,3,0,2,5,7,9,6,7,8,2,1,3,5,8,9,3,2.

Схема Эйлерова пути приведена на рис.1.4 (добавленные ребра показано пунктиром):

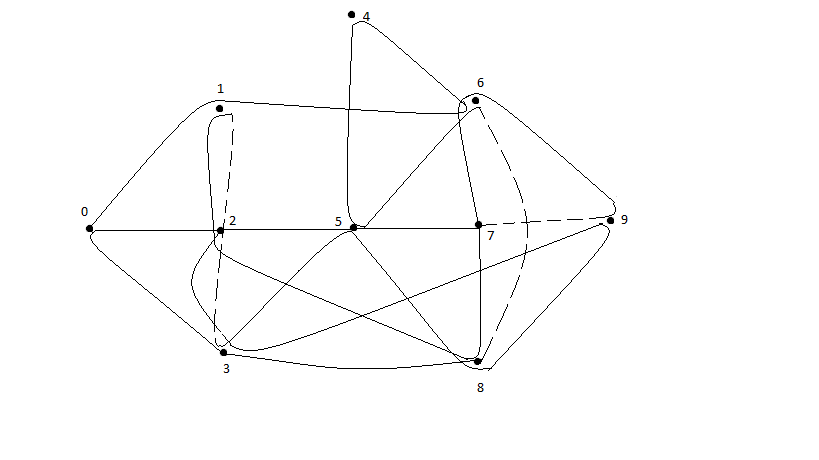
Рисунок 1.4 – Эйлеров путь, полученный путем добавления ребра

1.4.2 Эйлеров цикл

Эйлеров цикл позволяет обойти граф, проходя по каждому ребру только один раз. Незадействованных ребер быть не должно. Если такого цикла не существует, то в графе G добавить наименьшее число ребер таким образом, чтобы в новом графе можно было указать Эйлеров цикл.

Аналогично пункту 1.4.1 добавляем ребра {0,2},{1,3}, {6,8}, {7,9} замыкая Эйлерову цепь (при этом выполняя условие существования Эйлерова цикла - четность степеней всех вершин).

Полученный Эйлеров цикл: 0,1,6,4,5,6,8,3,0,2,5,7,9,6,7,8,2,1,3,5,8,9,3,2,0.

Схема Эйлерова цикла (добавленные ребра показаны пунктиром):

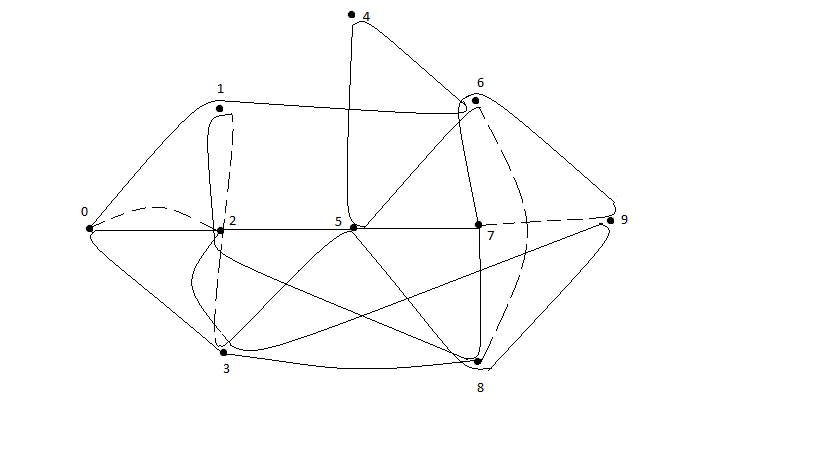
Рисунок 1.5 – добавление двух ребер для получения Эйлерова цикла