Алгоритми переведення чисел з однієї позиційної системи числення в іншу

1. Для переведення чисел із системи числення з основою p в систему числення з основою q, використовуючи арифметику нової системи числення з основою q, потрібно записати коефіцієнти розкладу, основи степенів і показники степенів у системі з основою q і виконати всі дії в цій самій системі. Очевидно, що це правило зручне при переведенні до десяткової системи числення.

Наприклад:

з шістнадцяткової в десяткову:

92C8₁₆=9*10₁₆³+2*10₁₆²+C*10₁₆¹+8*10₁₆⁰= 9*16₁₀³+2*16₁₀²+12*16₁₀¹+8*16₁₀⁰=37576

з вісімкової в десяткову:

735₈=7*10₈²+3*10₈¹+5*10₈⁰= 7*8₁₀²+3*8₁₀¹+5*8₁₀⁰=477₁₀

з двійкової в десяткову:

110100101₂=1*10₂⁸+1*10₂⁷+ 0*10₂⁶+1*10₂⁵+0*10₂⁴+0*10₂³+ 1*10₂²+0*10₂¹+1*10₂⁰= 1*2₁₀⁸+1*2₁₀⁷+0*2₁₀⁶+1*2₁₀⁵+ 0*2₁₀⁴+0*2₁₀³+1*2₁₀²+0*2₁₀¹+ 1*2₁₀⁰=421₁₀

2. Для переведення чисел із системи числення з основою p в систему числення з основою q з використанням арифметики старої системи числення з основою p потрібно:

• для переведення цілої частини:

  • послідовно число, записане в системі основою p ділити на основу нової системи числення, виділяючи остачі. Останні записані у зворотному порядку, будуть утворювати число в новій системі числення;

• для переведення дробової частини:

  • послідовно дробову частину множити на основу нової системи числення, виділяючи цілі частини, які й будуть утворювати запис дробової частини числа в новій системі числення.

Цим самим правилом зручно користуватися в разі переведення з десяткової системи числення, тому що її арифметика для нас звичніша.

Приклади: 999,35₁₀=1111100111,01011₂

для цілої частини:

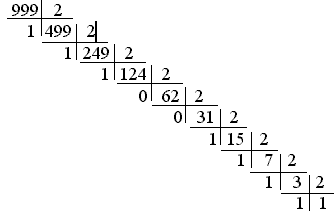
для дробової частини:

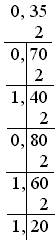
Систéма ч́ислення (number (numeration) system, notation) - сукупність способів і засобів запису чисел для проведення підрахунків.

Розрізняють 2 типи систем числення: позиційні і непозиційні. У позиційних системах числення позиція цифри впливає на її вагу у числі, наприклад у 1234 позиція цифри 1 = 3 (зправа наліво від 0) а позиція цифри 3 = 1 тоді як 1 - це кількість тисяч у числі а 3 - кількість десятків.

Основною характеристикою позиційної системи числення є її основа. Основа це кількість символів, що використовуються при записуванні чисел.

Типовим прикладом непозиційної системи числення є Римська система числення. Ми ж користуємося десятковою системою числення, тобто позиційною системою числення з основою 10.

У нумізматиці особливо велику вагу мають десяткова система, дванадцяткова (дуодецимальна), четвертна та шісткова системи. У ІТ застосовуються двійкова, десяткова, вісімкова, та шістнадцяткова системи.

47. Логічні елементи і, або, ні. Розв’язання логічних задач.

Числа можна порівнювати за допомогою звичайних операцій: дорівнює більше менше більше або рівне більше або рівне не дорівнює = > < >= <= <> x+y = 1.5 2*x > x+y x+y < x x*x > = 1.0 t < = 60.0 t < > 1.5 Літерні змінні (стрічки) порівнюються в лексикографічному порядку (за тим же принципом, що й слова у словнику): 'а'<'я', '1'<'2', 'мама'<'папа', 'мам'<'мама', '2'>'11' Порівняння можуть давати один із двох результатів: «так» (істинно, true) і «ні» (хибно, false). І ці результати порівнянь можна комбінувати, використовуючи логічні операції «і», «або», «не». (Переклад з англійської мови: і — and, або — or, не — not.) Приклад (n — ціле число, (х,у) — координати точки площини): 0 < = n and n < = 2 n = 0 or n = 1 not (n = 1 or n = 2) x = 0.0 or y = 0.0 x < > 0.0 and y < > 0.0 x > 0.0 and y > 0.0 x > 0.0 and x = y x*x+y*y < = 1.0 y > 0.0 and y < x and x * x + y * y < 1.0 множина з трьох цілих чисел 0,1,2; множина з двох цілих чисел 0,1; множина всіх цілих чисел, за вийнятком 1,2; множина точок на вісях координат; множина точок поза вісями координат; множина точок першого квандранта; бісектриса першого квандранта; одиничний круг з центром у початку координат; сектор одиничного круга, обмежного віссю х і бісектрисою першого квадратa