1. Тіктөртбұрыш бөлшектеуі. тік­төрт­бұрышы мен оның кесіндісінің нүктелері арқылы бөлінген бөлшектеуі және кесіндісінің нүктелері арқылы бөлшектеуі берілсін. Сонда А тіктөрбұрышы дербес , , , тіктөртбұрыштарына бөлінеді. А тіктөрбұрышының осылай бөліктеуін арқылы белгілейміз. Егер арқылы А тіктөрт­бұрышының ауданын белгілесек, онда (мұндағы ) және , өйткені

А тіктөрбұрышының Р бөліктеуін құрайтын және бөлшектеулерінің ең үлкенін бөлшектеуінің диаметрі деп атаймыз да, оны 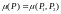ар­қылы белгілейміз. Сонымен .Төменгі және жоғарғы интегралдық қосындылар. А тіктөрбұры­шында шектелген 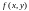функциясы берілсін, яғни болсын. А тіктөртбұрышының бөліктеуіне сәйкес тіктөртбұрышындағы функциясының мен мәндерін сәйкес арқылы белгілейік, яғни 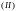Сонда бұлардың көмегімен түзілген 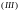қосындыларын сейкес Риманның жоғарғы, төменгі қосындылары деп атайды. Олардың мынадай екі қасиетін атап өтейік. 1-қасиет. Егер А тіктөртбұрышында (I) орындалса, онда

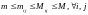
Және Дәлелдеу. Шынында да А тіктөртбұрышында орындалатын теңсіз­дік­тер барлық тіктөртбұрыштарында да орындалады. Сондықтан және сан­дары функциясының жиындарында қабылдайтын мәндері жиын­дарының да сәйкес төменгі, жоғары шекаралары болады. Ал анықтаудан шығады да, оларды санына көбейтіп, сонан соң қосындыласақ

Енді анықтауларымызды ескерсек, теңсіздіктерге келеміз. 2-қасиет. А тіктөртбұрышының кез келген бөлшектеуі үшін , Дәлелдеуі айқын, өйткені , қосындыларында десек, онда болатын қосындылармен ғана шектелуге болады.

2.Екі еселі Риман интегралының тіктөртбұрыш бойынша анықтамасы. Айталық функциясы А тіктөртбұрышында анықталған және онда шектел­ген болсын. А тіктөртбұрышының барлық мүмкін бөліктеулері бойынша құрылған қосындылар жиынының инфимумын жоғарғы интеграл, ал төменгі қосындылар жиынының супремумын төменгі интеграл деп атап, сәйкес арқылы белгілейді, яғни Сонда теңсіздіктерден Бұл шектелген функциясының әрқашанда төменгі де, жоғарғы да инте­гралдарының бар және олардың нақты сан екенін көрсетеді. Егер А тіктөртбұрышында анықталған және шектелген фкнуциясы үшін теңдігі орындалса, онда функциясы А тіктөртбұрышында Риман бойынша интегралданады деп, ал жоғарғы және төменгі интегралдардың ортақ мәнін функциясының А бойынша екі еселі Риман интегралы деп атап, немесе арқылы белгілейді. Кейде екі еселі Риман интегралын

түрінде де белгілейді.

3. Екі айнымалыдан тәуелді шектелген функцияның Риман бойынша интегралданбайтыны туралы мысал.Төмендегі мысал кез келген шектелген функцияның интегралдана бер­мей­тінін көрсетеді. шаршысында

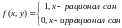_(I) функциясы мен А шаршысының бөлшектеуі берілсін. Егер болса, онда кесіндісінде әрқашанда рационал нүкте мен иррационал нүкте табылады, демек кез келген , және үшін ,

Сонда ,

Ал бойынша .

Мұнан теңдіктің орындалмайтынын көреміз, өйткені Сондықтан интегралдану анықтамасы бойынша _(I) функция А шаршы­сында интегралданбайды.

4. Тұрақты функциясының тіктөртбұрышта интегралдануы.

тіктөртбұрышында анықталған функциясы берілсін. Онда А тіктөртбұрышының кез келген бөліктеуінде кез келген тіктөрбұрышындағы ең үлкен және ең кіші мәндері болады. Сондықтан

,

Демек, ,

Бұдан теңдік орындалса және белгілеу бойынша

5. Интегралдық қосынды монотондығы Егер бөлшек­теуі бөлшектеуінің ұсақтауы болса, онда

(1) яғни бөлшектеуді ұсақтаудан төменгі қосынды кемімейді, ал жоғарғы қосынды өспейді. Дәлелдеуді мұның төменгі қосындысы үшін ғана жүргіземіз, ал екіншісі дәл солай дәлелденеді. Ең қарапайым жағдайды қарастырайық. Айталық, бөлшектеуінің Р бөлшектеуінен тек бір ғана нүктесі артық ұсақтауы болсын және оның ол нүктесі және нүктелерінің арасында жатсын. Сонымен бірге,

болсын. Ал жиын кеңейген сайын оның инфимумы кеми түсетін болғандықтан Үшін (2)Демек,

яғни , жағдайында (1) теңсіздіктерінің біріншісі дәлелденді. Егер бөлшектеуінің Р бөлшектеуінен өзгешелігі нүкте болса (мысалы, бөлшектеуі бөлшектеуінен өзгешелігі нүкте, ал бөлшектеуі бөлшектеуінен өзгешелігі нүкте, яғни болсын), онда дәлелденген жағдайды рет қайталап, (1) теңсіздіктердің біріншісінің жалпы жағдайда да орындалатынын көреміз.

6. Төменгі интегралдық қосындының жоғарғы интегралдық қосындыдан аспауы Кез келген жоғарғы интегралдық қосынды кез келген төменгі интегралдық қосындыдан кем емес, яғни кез келген шектеулі функциясы мен кез келген және бөлшектеулері үшін

(3) Дәлелдеуі. Егер десек, онда бөлшектеуі және бөлшектеулерінің әрқайсысының ұсақтауы болады, Егер бөлшек­теуі бөлшектеуінің ұсақтауы болса, онда яғни бөлшектеуді ұсақтаудан төменгі қосынды кемімейді, ал жоғарғы қосынды өспейді.

7. Шектеулі функция жоғарғы интегралының төменгі интегралдан кем болмауы Әрбір шектеулері функциясының жоғарғы интегралы оның төменгі интегралынан кем емес, яғни

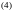
Дәлелдеу. Белгілі бір бөлшектеуін алайық. Онда Төменгі интегралдық қосындының жоғарғы интегралдық қосындыдан аспауы туралы лемма бойынша қандай да бір бөлшектеуін алмайық. демек, саны барлық төменгі қосындылардың жоғарғы шекараларының бірі, ал сондай шекаралардың ең кішісі болғандықтан . Енді кез келген бөлшектеу деп қарастырайық, онда саны барлық жоғарғы қосындылардың төменгі шекараларының бірі екенін көреміз және санының сондай шекаралардың ең үлкені болғандықтан

теңсіздігіне келеміз.

8. Шектеулі функция Риман бойынша интегралдану критерийі

тіктөртбұрышында шектеулі функциясының Риман бойынша интегралдануы үшін кез келген 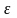оң санына сәйкес

(1) теңдігі орындалатындай сегментінен , ал сегментінен бөлшектеулерінің табылуы қажетті және жеткілікті. Дәлелдеуі. Қажеттілігі. Айталық, функциясы тіктөртбұры­шында Риман бойынша интегралданады, яғни болсын. Онда супремум мен инфимум анықтамалары бойынша кез келген оң саны үшін

(2)

теңсіздіктерін қанағаттандыратын бөлшектеулері табылады. Егер біз бөлшектеуі үшін бөлшектеулерінің ұсақтауын алсақ, яғни

десек, онда Интегралдық қосынды монотондығы туралы лемма бойынша және (2) теңсіздіктерден

яғни

демек, (1) теңсіздік дәлелденді. Жеткіліктігі. Кез келген оң саны үшін бөліктеуі табылып, (1) теңсіз­дік орындалсын. Онда жоғарғы және төменгі интегралдардың анықтамасы бойынша

₍₃₎

Бұлардың ең шеткі өрнектеулерінің айырымы олардың ортасындағы кезкелген екеуінің айрымынан кем емес, демек, (3) және (1) теңсіздіктерден

мұнан ал бұл функция интегралдануының анықтамасы бойныша функциясы интегралданады деген сөз. Бұл критерийді қысқаша логикалық символикалар арқылы былай жазуға болады: мұндағы, функциясы аймағына Риман бойынша интегралданады дегенді білдіреді.

9. Жиын бойынша алынған екі еселі интеграл. Қасиеттері Айталық жазықтығының шектелген жиыны болсын. жиынын ұстайтын, яғни 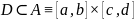болатындай тіктөртбұрышын алайық. Егер функциясы жиынында анықталған болса, онда функциясын енгіземіз. Егер функциясы тіктөртбұрышында интегралданса,онда функциясын жиынында интегралданады деп айтамыз. Сонымен, функциясының жиыны бойынша Риман интегралы теңдігі арқылы анықталады. Екі еселі интегралдың төмендегі келтірілген қасиеттері тура бір айныма­лы­ның функциясының Риман интегралының сәйкес қасиеттеріндегідей дәлелденеді.

I. Егер функциясы 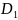және жиындарында интегралданса және

Ø болса, онда бұл функция жиынында да интегралданады әрі

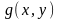
II. Егер функциясы жиынында интегралданса, онда (мұндағы ) функциясы да жиынында интегралданады әрі III. Егер және функциялары жиынында интегралданса, онда олардың алгебралық қосындысы осы жиынында интегралданады әрі

IV. Егер және функциялары жиынында интегралданса, онда олардың көбейтіндісі де осы жиынында интегралданады.V. Егер жиынында интегралданатын және функциялары осы жиында теңсіздігін қанағаттандырса, онда VI. Егер функциясы жиынында интегралданса, онда функ­циясы да осы жиында интегралданады әрі VII. Орта мән туралы теорема. Егер және функциялары жиынында интегралданса әрі барлық үшін болса, онда

теңдігін қанағаттандыратын кесіндісінен саны табылады.