Билет 8

Кинематика вращательного движения

При описании вращательного движения твердого тела относительно неподвижной в данной системе отсчета принято использовать векторные величины особого рода. В отличие от рассмотренных выше полярных векторов r (радиус-вектор), v (скорость), a (ускорение), направление которых естественным образом вытекает из природы самих величин, направление векторов, характеризующих вращательное движение, совпадает с осью вращения, поэтому их называют аксиальными (лат. axis – ось).

Элементарный поворот dφ – аксиальный вектор, модуль которого равен углу поворота dφ, а направление вдоль оси вращения ОО' (см. рис. 1.4) определяется правилом правого винта.

  Рис.1.4. К определению направления аксиального вектора

Линейное перемещение dr произвольной точки А твердого тела связано с радиусом-вектором r и поворотом dφ соотношением dr=rsinα•dφ или в векторном виде через векторное произведение:

dr=[dφ,r] (1.9)

Соотношение (1.9) справедливо именно для бесконечно малого поворота dφ.

Угловая скорость ω – аксиальный вектор, определяемый производной вектора поворота по времени:

ω=dφ/dt=φ'

Вектор ω, как и вектор dφ, направлен вдоль оси вращения по правилу правого винта (рис.1.5).

  Рис.1.5. К определению направления вектора

Угловое ускорение β – аксиальный вектор, определяемый производной вектора угловой скорости по времени:

β=dω/dt=d²φ/dt²=ω'=φ''

При ускоренном движении вектор β по направлению совпадает с ω (рис. 1.6,а), а при замедленном - векторы β и ω направлены противоположно друг другу (рис. 1.6,б).

  Рис.1.6. Связь между направлениями векторов ω и β

Важное замечание: решение всех задач на вращение твердого тела вокруг неподвижной оси по форме аналогично задачам на прямолинейное движение точки. Достаточно заменить линейные величины x, v_x, a_x на соответствующие им угловые φ, ω и β, и мы получим уравнения, аналогичные (1.6) -(1.8).

Угловая и линейная скорость

Угловая скорость - векторная величина: характеризующая вращательное движение твердого тела и направленная по оси вращения согласно правилу правого винта.Отношение угла поворота к соответствующему времени измеряет угловую скорость вращения.

За единицу угловой скорости на практике принимают оборот в секунду или оборот в минуту, то есть угловую скорость такого равномерного вращения, в котором тело за единицу времени (секунду или минуту) делает один полный оборот вокруг оси. В системе СИ единицей угловой скорости является радиан в секунду, представляющая угловую скорость, при которой каждая точка тела за 1 секунду проходит путь, равный ее расстоянию от оси вращения.

ω = 2πn

 

где: ω - угловая скорость в 1/секунду, n – число оборотов в секунду, N – число оборотов минуту. Если Т – период вращения (время, за которое тело совершает полный оборот), то формула ω = 2πnпринимает вид:

 

Линейная скорость при вращении:

Скорость, с которой движется отдельная точка вращающегося тела, называется линейной скоростью. Она выражается формулами: v = ω r ω =2πrn, где:

ω – угловая скорость вращения в 1/сек,

r – расстояние точки от оси вращения.

Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости материальной точки.

При вращении точки вокруг неподвижной оси, угловое ускорение по модулю равно^[1]:

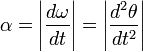
Вектор углового ускорения   направлен вдоль оси вращения (в сторону   при ускоренном вращении и противоположно   — при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости   по времени^[2], то есть

,

и направлен по касательной к годографу вектора   в соответствующей его точке.

Существует связь между тангенциальным и угловым ускорениями:

,

где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени.

Угловое ускорение измеряется в рад/с².