9. Сызықты біртекті жүйелер.

(i=1,2,…,m) жүйенің бос мүшелерінің бәрі нолге тең болса, (i=1,2,…,m) (2) жүйе біртекті жүйе деп аталады.

Біртекті теңдеулер жүйесін шешейік, .Шешуі. Біртекті жүйе әруақытта үйлесімді, себебі жүйенің нолдік шешуі бар. Ендік нолдік емес шешулері бар жоқтығын анықтайық. Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:

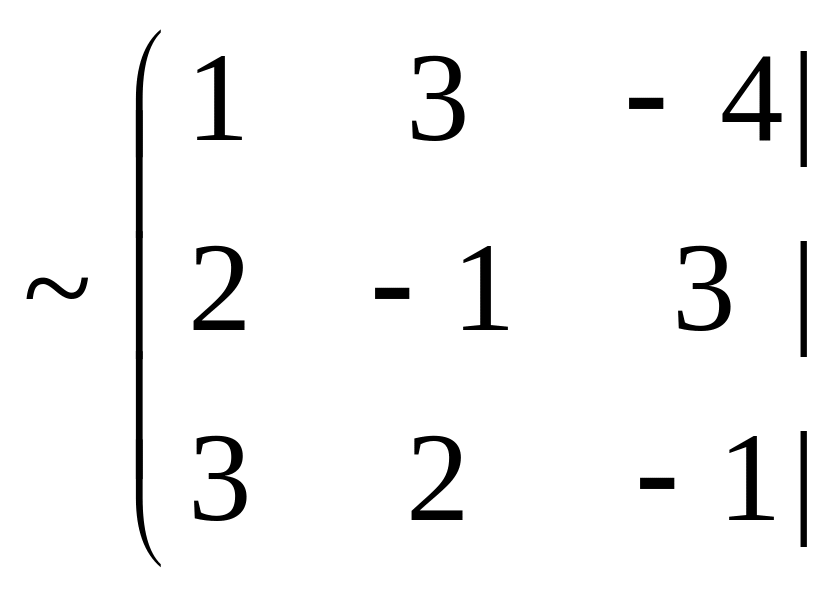
11. Аналитикалық геометрияның қарапайым үш есебі. Екі нүкте ара қашықтығы.Жазықтықта және екі нүкте берілсін. Осы екі нүкте арақашықтығын, немесе АВ кесіндісінің ұзындығын, мына формуламен есептейді:

.2. Кесіндіні берілген қатынаста бөлу. Жазықтықта және екі нүкте берілсін. АВ кесіндісін АМ:МВ= болатындай қатынаспен бөлетін М(х,у) нүктесінің координаталары мынадай формуламен есептелінеді: , .Дербес жағдайда, АВ кесіндісін тең екіге бөлу керек болса, яғни =1:1=1, формула былай түрленеді: , .3. Үшбұрыш ауданы. Жазықтықта төбелері , , болатын үшбұрыш ауданы мынадай формуламен есептелінеді: . Сипаттамалық теңдеуін жазсақ: , немесе 2-14 +13=0; теңдеу түбірлері түрлендірудің сипаттамалық сандарыболады, , . сипаттамалық санға сәйкес өзіндік векторларды табу үшін мынадай теңдеулерді шешеміз: (A- Е)

Х = 0. Ашып жазсақ, болғандықтан теңдеулер жүйесі мынадай түрге келеді: Жүйеден екендігі шығады. деп алсақ, жүйе шешімі болады. Кез келген үшін сипаттамалық санға сәйкес өзіндік вектор табылды. Дәл осылай кез келген үшін сипаттамалық санға сәйкес келетін өзіндік вектор табылады.

12. Жазықтықтағы түзу теңдеулері. Жазықтықтағы түзу (1-сурет) Оу осін В(0;b) нүктесінде қиып, Ох осімен (0< < ) бұрыш жасасын. Түзу бойынан қандай да бір М(х,у) нүкте алайық. Түзудің Ох осімен жасаған бұрышының тангенсін ВМК үшбұрышынан табамыз: деп белгілеп, түзудің бұрыштық коэффициенті деп атау қабылданған. Сонымен .Осы қатынастан у-ті тапсақ:y=kx+b Түзу бойында жатқан кез келген нүктенің координатасы (2) теңдеуді қанағаттандырады да түзуден тыс жатқан нүктелер бұл теңдеуді қанағаттандырмайды. (2) теңдеу түзудің бұрыштық коэффициентімен берілген теңдеуі деп аталады.Дербес жағдайларын қарастырайық

1.Түзудің бұрыштық коэффициентімен берілген теңдеуіндегі b=0 болсын. Онда түзу теңдеуі y=kx түрге келеді де, түзу координат басынан өтеді

2. Егер болса, онда болады да, түзу теңдеуі y=b түрге келеді де, түзу Ох осіне параллель болады (3-сурет). Ал Ох осінің теңдеуі y=0 болады.

3. Егер болса, онда мәні болмайды, түзу Ох осіне перпендикуляр болады. Айталық түзу Ох осінен а тең кесінді қиып өтеді, сонда түзу теңдеуі х=а түрде болады (4-сурет). Ал Оу осінің теңдеуі х=0 болады.

Мынадай теорема айтуға болады.Теорема. Тік бұрышты координаталар жүйесінде кез келген түзу бірінші ретті теңдеумен беріледі Ах+Ву+С=0 Және керісінше, (3) теңдеу (А, В, С коэффициенттердің бәрі бір мезгілде нолге тең болмаған кезде) тік бұрышты координаталар жүйесінде қандай да бір түзуді анықтайды. теңдеуді әдетте түзудің жалпы теңдеуі деп атайды.

Берілген бағыт және берілген нүкте арқылы өткен түзу теңдеуі. Көп жағдайда түзу теңдеуін оның бойында жатқан белгілі нүкте мен k бұрыштық коэффициенті арқылы жазу керек болады

Түзу теңдеуін (2) түрінде жазайық, y=kx+b, мұндағы b әзірше белгісіз. Түзу нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y₁=kx₁+b.Осы теңдіктен белгісіз b табылады, b = y₁ - kx_1. Табылған мәнді теңдеудегі орнына қойып, берілген бағыт және берілген нүкте арқылы өткен түзу теңдеуін аламыз: y =k(x – x₁)+ y₁ Егер (4) теңдеудегі k ерікті мән қабылдаса, онда теңдеу нүктесі арқылы өтетін түзулер шоғының теңдеуін анықтайды .Берілген екі нүкте арқылы өткен түзу теңдеуі. және нүктелері берілсін. АВ түзуінің теңдеуін жазу үшін А нүктесі арқылы өткен түзулер шоғының теңдеуін жазамыз:

y =k(x – x₁)+ y_1.

АВ түзуі нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y₂ =k(x₂ – x₁)+ y_1. Осы теңдіктен белгісіз k табылады, . Табылған мәнді теңдеудегі орнына қойып, берілген екі нүкте арқылы өткен түзу теңдеуін аламыз: .

Т үзудің “кесіндідегі” теңдеуі. Түзу Ох осінен а-ға тең, Оу осінен b-ға тең кесінді қиып өтсін (8-сурет). Түзу А(а;0) және В(0;b) нүктелері арқылы өтеді деп, (5) теңдеуді қолданайық. Сонда түзу теңдеуі мынадай түрде жазылады:

Енді ықшамдасақ, түзудің “кесіндідегі” теңдеуін аламыз:

Екі түзу арасындағы бұрыш. Екі түзу берілсін: y=k₁x+b₁, y=k₂x+b₂. Мұндағы , . Екі түзу арасындағы бұрышты табу керек (9-сурет).

Суреттен көрініп тұрғандай . Осыдан

13. түзулердің параллельдік және перпендикуляр шарттары. Нүктеден түзуге дейінгі қашықтық Егер екі түзу параллель болса, онда =0 болады да tg =0. Бұл жағдайда (7) формула мынадай түрге келеді: k₂ – k₁ = 0. Осыдан екі түзудің параллелдік шарты шығады: k₂ = k₁, яғни екі түзудің бұрыштық коэффициенттері тең болса, ол түзулер параллель болады және керісінше. Егер екі түзу перпендикуляр болса, онда болады да, , . Осыдан екі түзудің перпендикулярлық шарты шығады k₂= , яғни екі түзудің бұрыштық коэффициенттері мәндері бойынша кері, таңбалары бойынша қарама-қарсы болса, ол түзулер перпендикуляр болады және керісінше.

Нүктеден түзуге дейінгі қашықтық. Тікбұрышты координаталар жүйесінде қандай да бір түзу Ах+Ву+С=0 және түзуден тыс жатқан нүкте М(х₀,у₀) берілсін (10-сурет).

Нүктеден түзуге дейінгі қашықтық деп нүктеден түзуге түсірілген перпендикуляр ұзындығын айтамыз. Суретте ол d=MN. Осы ара қашықтықты табу үшін: а) Берілген түзуге перпендикуляр және М(х₀,у₀) нүктесі арқылы өтетін түзу теңдеуін тауып аламыз; б) Б ерілген түзу мен MN түзулерінің теңдеуін жүйе етіп шешіп, олардың қилысу нүктесі N табамыз; в) екі нүктенің ара қашықтығын есептейтін формула көмегімен d=MN ара қашықтықты есептейміз. Нәтижесінде мынадай формула алынады:

Мысал. Төбелері А(1;1), В(7;4), С(4;5) болатын үшбұрыштың а) АВ қабырғасының ұзындығын; б) АВ және АС түзулерінің теңдеуін;в) А ішкі бұрышын; г) С төбесінен жүргізілген биіктік пен медиана теңдеулерін;д

) С төбесінен АВ қабырғасына дейінгі қашықтықты табу керек.

Ш ешуі. а) Кесінді ұзындығын есептейтін формула бойынша АВ қабырғасының ұзындығын есептейміз:

б) АВ түзуінің теңдеуін формуланы пайдаланып табамыз. Мұндағы және нүктелер А және В нүктелерінің координаталары болады: , ықшамдасақ,

теңдеуін аламыз Дәл осы жолмен АС түзуінің теңдеуін аламыз: , осыдан . в) А ішкі бұрышын есептеу үшін (7) формуланы пайдаланамыз. Ол үшін АВ және АС түзулерінің коэффициенттерін алдыңғы пункттегі теңдеулерінен аламыз да, , , формулаға қоямыз: , осыдан .

г) С төбесінен жүргізілген биіктікті СD дейік. СD теңдеуін жазу үшін y =k(x – x₁)+ y₁ теңдеуді пайдаланамыз. нүктенің орнына С нүктесінің координатасын қойсақ осы нүкте арқылы өтетін түзулер шоғының теңдеуін аламыз: y =k(x -4)+ 5. Осы шоқтан АВ түзуіне перпендикуляр түзу теңдеуін таңдап алу үшін СD биіктіктің АВ түзуге перпендикуляр болатынын ескеріп табылады да, түзулер шоғы теңдеуіндегі орнына қойылады: y =-2(x -4)+ 5 _. Ықшамдап СD биіктік теңдеуін аламыз, y =-2x+13. СЕ медиана теңдеулерін жазу үшін АВ кесіндісінің ортасында жатқан Е нүктесінің координаталарын табамыз:

, , Е=(4; 2,5). Екі нүкте арқылы өткен түзу теңдеуін пайдаланып медиана теңдеуін аламыз: , осыдан х=4 СЕ теңдеуі болады.

д) С төбесінен АВ қабырғасына дейінгі қашықтықты табу үшін, АВ теңдеуін x - 2y + 1 = 0 түрінде жазып алып, (10) формуланы пайдаланамыз: .

14. Векторлық кеңістік. Векторларға жүргізілетін сызықты амалдар.R жиынның элементтерін қосу және элементін нақты санға көбейту амалдары төмендегідей шарттарды қанағаттандырса, R жиын векторлық (сызықтық) кеңістік деп, ал элементтерін векторлар деп атайды:

1. x+y=y+x;2.(x+y)+z=x+(y+z);

3.Кез келген x R үшін 0 R (нол-элемент) табылады да, мынадай қатынас орындалады: x+0=x;

4.Кез келген x Rүшін -х R (қарама-қарсы элемент)табылады да, мынадай қатынас орындалады: x+(-x)=0;

5. x=x; 6. ( x)=( )x;

7. (x+y)= x+ y 8. ( + )x= x+ x.

х ж-е y векторларының айырмасы деп х векторы мен –1у векторларының қосындысын айтамыз: x-y=x+(-1)y Векторлық кеңістіктің анықтамасынан кез келген х векторды 0 нақты санына көбейткенде пайда болатын жалғыз 0 - ноль вектордың бар болатындығы; әрбір х вектор үшін осы векторды (-1) санына көбейткенде пайда болатын жалғыз қарама-қарсы ( –х) вектордың бар болатындығы шығады

15. Сызықты тәуелді және сызықты тәуелсіз векторлар.R сызықты кеңістіктің векторларыx, y, z, …, u болсын. Мынадай v= x+ y+ z+…+ u теңдікпен анықталған v векторы осы кеңістікте жатады, мұндағы -нақты сандар. Осы v векторды x, y, z, …, u векторларының сызықты комбинациясы деп атайды. Айталық x, y, z, …, u векторларының сызықты комбинациясы 0 ноль вектор болсын, яғни x+ y+ z+…+ u= 0. Анықтама.(1) теңдік барлық = = =…= =0болған кезде ғана орындалса х, y, z, …, u векторлары сызықты тәуелсіз деп аталады. Ал егер (1) теңдік , , ,…, сандарының ең болмағанда біреуі нолден өзгеше болғанда орындалса х, y, z, …, u векторлары сызықты тәуелді деп аталады.Мынадай тұжырымның дұрыстығына көз жеткізу қиын емес: Егер x, y, z, …, u векторлар сызықты тәуелді болса, онда бұл векторлардың біреуі басқаларының сызықты комбинациясы арқылы жіктеледі. Және керісінше, егер x, y, z, …, u векторлардың біреуі басқаларының сызықты комбинациясы арқылы жіктелсе, онда бұл векторлар сызықты тәуелді болады.Жазықтықтағы коллинеар емес екі вектор сызықты тәуелсіз векторға мысал болады. Шынында да, жазықтықтағы және векторлары үшін (1) теңдік + =0 тек = =0 болғанда ғана орындалады. Ал, олай демесек, мысалы болса,онда =- болып, пен векторларының коллинеарлығын білдірген болар еді. Ал бірақ жазықтықтағы кез келген үш вектор сызықты тәуелді болады. Векторлық кеңістіктің қасиеттері:1.Егер x, y, z, …, u векторларының ішінде ноль-вектор бар болса, онда бұл векторлар сызықты тәуелді болады. Шынында да, егер, мысалы, x=0 болса, онда (1) теңдік =1, = =…= =0 болғанда орындалады. 2. Егер x, y, z, …, u векторларының қандай да бір бөлігі сызықты тәуелді болса, онда бұл векторлардың бәрі сызықты тәуелді болады. Шынында да, мысалы, y, z, …, u векторлары сызықты тәуелді болсын десек y+ z+…+ u=0 теңдік , ,…, сандарының бәрі бір мезгілде нолге тең болмағанда орындалып тұр деген сөз. Олай болса бұл теңдік сол , ,…, сандары және =0саныменде орындалады.Мысал қарастырайық. x=(3,2,-1), y=(2,-1,3), z=(1,3,-4) векторлары сызықты тәуелді ме ? Шешуі. x, y, z векторлары сызықты тәуелді болады, егер x+ y+ z= 0 теңдігі , , сандарының ең болмағанда біреуі нолден өзгеше болғанда орындалса. x, y, z векторларын бағана түрінде жазып, теңдікті ашып жазайық: + + = 0 Есеп мынадай жүйені шешуге келтірілді.

Ж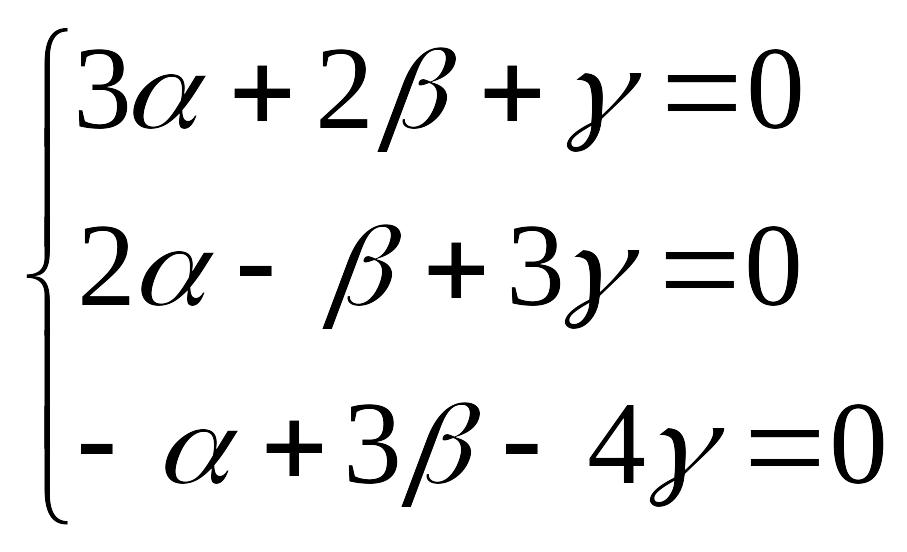 үйе біртекті, яғни оның нолдік шешімі әруақытта бар. Жүйені Гаусс әдісімен шешіп жүйенің нолдік емес шексіз көп шешімін табуға болады: , , мұндағы С-ерікті нақты сан. Сонымен, берілген векторлар үшін (1) теңдік , , сандарының ең болмағанда біреуі нолден өзгеше болғанда (айталық, , (С=1)) орындалып тұр, олай болса берілген векторлар сызықты тәуелді. Анықтама.Егер R сызықты кеңістікте n сызықты тәуелсіз вектор бар болып, ал осы кеңістіктің кез келген n+1 векторы сызықты тәуелді болса, онда R кеңістікті n өлшемді деп атайды. Кейде кеңістік өлшемі n-ге тең дейді де, dim(R)=n деп немесе Rⁿ деп жазады.

16.Кеңістіктегі базис ұғымы. Векторды базис бойынша жіктеу. Анықтама. п өлшемді векторлық кеңістіктің п сызықты тәуелсіз векторларының жиыны базис деп аталады.Мынадай тұжырымдар дұрыс болады: 1. Егер қандай да бір векторлар базис құрса, онда осы векторлардың координаталарынан құрылған анықтауыш нолден өзгеше болады.2. п өлшемді векторлық кеңістіктің әр бір векторы базистік векторлардың сызықты комбинациясы арқылы жазылады және бұл жазу жалғыз болады. Сонда, егер - кеңістіктің базисі болса, онда кез келген x R векторы жалғыз түрде былай жазылады: .Демек базисінде х векторы сандарымен жалғыз түрде анықталады. сандар х векторының осы базистегі координаталары деп аталады. Мысал. x=(1;3;0), y=(-1;2;1), z=(1;-1;2) векторлары базис құра ма? Егер құрса u=(2;0;1) векторын (x,y,z) базисі бойынша жікте (яғни, u векторын x, y, z векторларының сызықты комбинациясы арқылы жазу керек).Шешуі. Бірінші тұжырым бойынша x, y, z векторлары базис құрса, онда осы векторлардың координаталарынан құрылған анықтауыш нолден өзгеше болуы керек: Демек, x, y, zвекторлары базис құрады екен.Екінші тұжырым бойынша u векторы (x,y,z) базисте жіктеледі және ол жіктелу жалғыз болады: .x, y, z, u векторларын бағана түрінде жазып, теңдікті ашып жазайық:

+ + = Есеп мынадай жүйені шешуге келтірілді: Осы жүйені шешіп u векторының (x, y, z) базисіндегі ( , , ) координаталарын табамыз. Үш белгісізді үш теңдеуден тұрған жүйені жүйе шешудің кез келген әдісімен шешуге болады. Сонда мынадай жалғыз шешім аламыз: , , . Сонымен,