
- •1.Матрицалар және оларға амалдар қолдану.
- •6.N белгісізді m теңдеуден тұратын жүйе, Крамер ережесі. N белгісізді m теңдеуден тұратын жүйе деп мынадай жүйені айтады: (1)
- •9. Сызықты біртекті жүйелер.
- •17.Функция ұғымы. Функция шегі
- •18. Тамаша екі шек және салдары.
- •20. Шектің экономикалық қолданыстары
- •24. Логарифмдік дифференциалдау. Жоғары ретті туынды.
- •27. Ферма, Ролль, Лагранж теоремалары
- •28. Туындының экономикалық қолданыстары. Функция иілгіштігі
- •37. Көп айнымалыдан тәуелді ф-ия. Анықталу обл. Деңгейлік сызықтар
- •39. Бағыт бойынша туынды ж-е градиент
- •44. Бірінші ретті сызықты дифференциалдық теңдеулер. Мысалдар.
- •47. Комбинаторика элементтері
- •48. Ықтималдықтардың қосу және көбейту теоремалары.
- •49. Шартты ықтималдық. Тәуелді оқиғалар
- •54. Үзіліссіз кездейсоқ шама. Ықтималдықтардың үлестірім заңдылығы және негізгі сандық сипаттамалар.
- •56. Бірқалыпты үлестіру
- •61. Сенімділік ықтималдық, сенімділік интервалы
1.Матрицалар және оларға амалдар қолдану.
Анықтама. m жатық n тік жолдан құрылған кестені mxn өлшемді матрица деп атайды. Матрицаны құрайтын сандар матрица элементтері деп аталады. Әдетте матрица латын алфавитінің бас әріптерімен, ал элементтері сәйкес кіші әріптермен белгіленеді:
 Матрица
элементінің бірінші индексі жатық жол
нөмірі, ал екінші индексі тік жол (бағана)
нөмірін көрсетеді. Бір ғана жатық жолдан
құралған матрицаны жол-матрица,
ал бір
ғана тік жолдан құралған матрицаны
бағана-матрица
депатайды:
Матрица
элементінің бірінші индексі жатық жол
нөмірі, ал екінші индексі тік жол (бағана)
нөмірін көрсетеді. Бір ғана жатық жолдан
құралған матрицаны жол-матрица,
ал бір
ғана тік жолдан құралған матрицаны
бағана-матрица
депатайды:
![]() - жол-матрица;
- жол-матрица;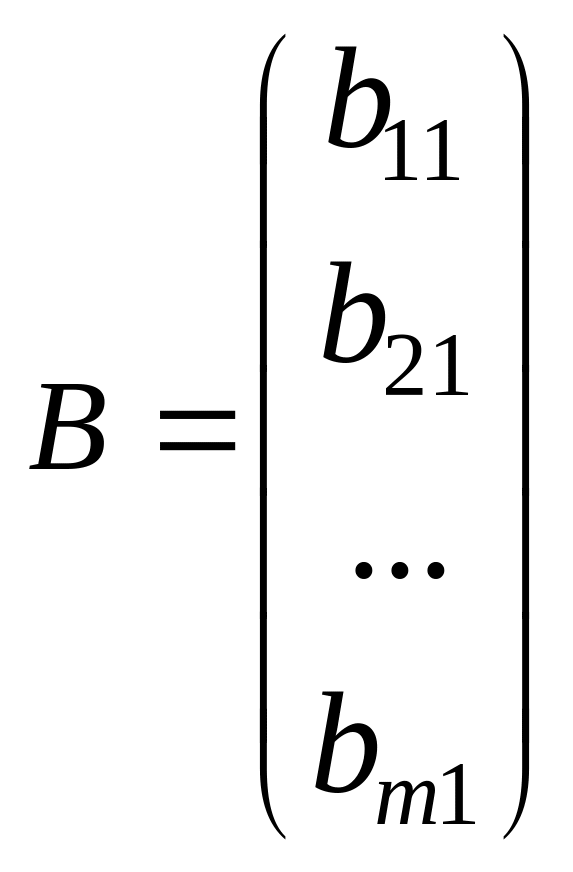 -
бағана матрица. Жол матрица мен бағана
матрицаны кейде вектор деп те айтады..Жатық
жолдар саны мен тік жолдар саны тең
болатын матрица квадрат
матрица
деп аталады, Квадрат матрицаның
-
бағана матрица. Жол матрица мен бағана
матрицаны кейде вектор деп те айтады..Жатық
жолдар саны мен тік жолдар саны тең
болатын матрица квадрат
матрица
деп аталады, Квадрат матрицаның
![]() элементтері диагоналдық
элементтер деп
аталады да, матрицаның негізгі
диагоналін құрайды.
Ал
элементтері диагоналдық
элементтер деп
аталады да, матрицаның негізгі
диагоналін құрайды.
Ал
![]() элементтері қосымша
диагоналдық элементтер деп
аталады да, матрицаның қосымша
диагоналін құрайды.
Квадрат матрицаның негізгі диагоналінің
астындағы немесе үстіндегі элементтері
нолге тең болса, матрица үшбұрышты
матрица
деп аталады
элементтері қосымша
диагоналдық элементтер деп
аталады да, матрицаның қосымша
диагоналін құрайды.
Квадрат матрицаның негізгі диагоналінің
астындағы немесе үстіндегі элементтері
нолге тең болса, матрица үшбұрышты
матрица
деп аталады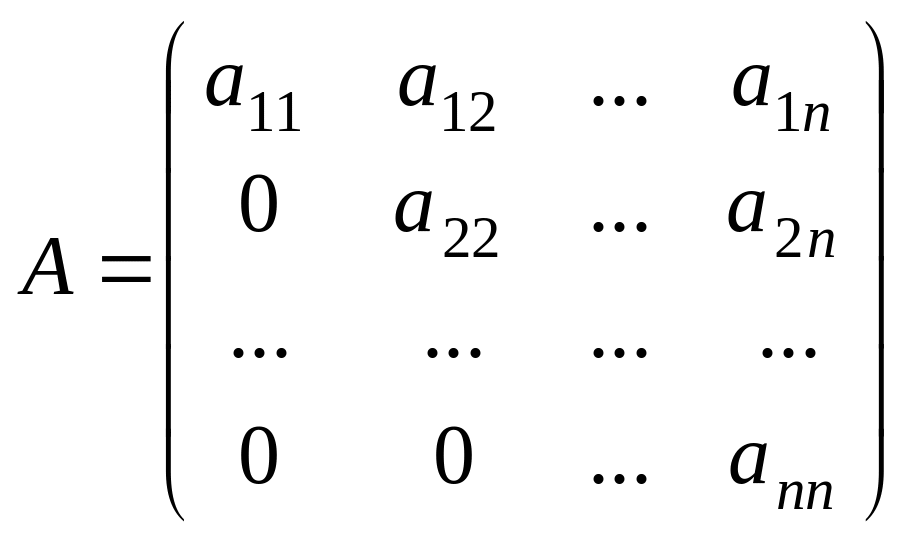 ,
,
 Диагоналды
емес элементтерінің бәрі нолге тең
болатын квадрат матрица диагоналды
матрица
деп аталады,
Диагоналды
емес элементтерінің бәрі нолге тең
болатын квадрат матрица диагоналды
матрица
деп аталады,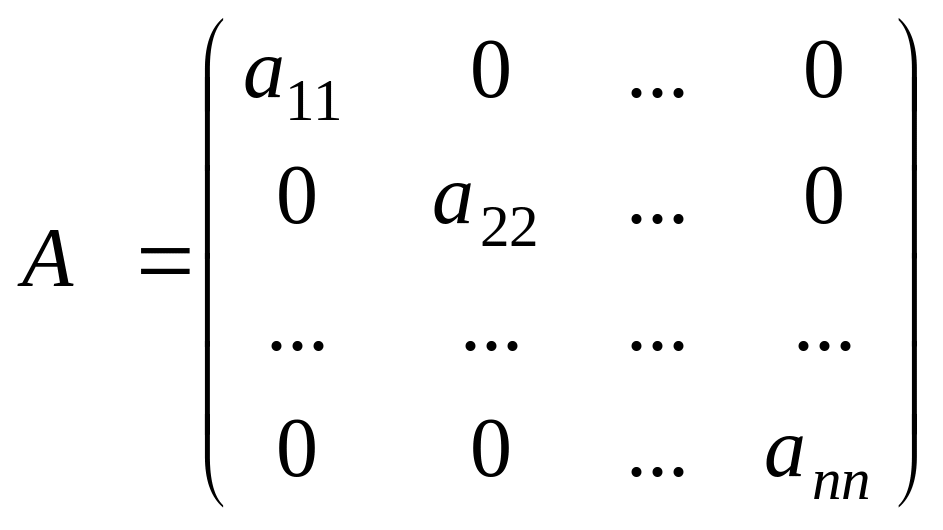 Барлық
диагоналды элементтері бірге тең болатын
диагоналды матрица бірлік
матрица
деп аталады және оны Е әрпімен
белгілейді,
Барлық
диагоналды элементтері бірге тең болатын
диагоналды матрица бірлік
матрица
деп аталады және оны Е әрпімен
белгілейді,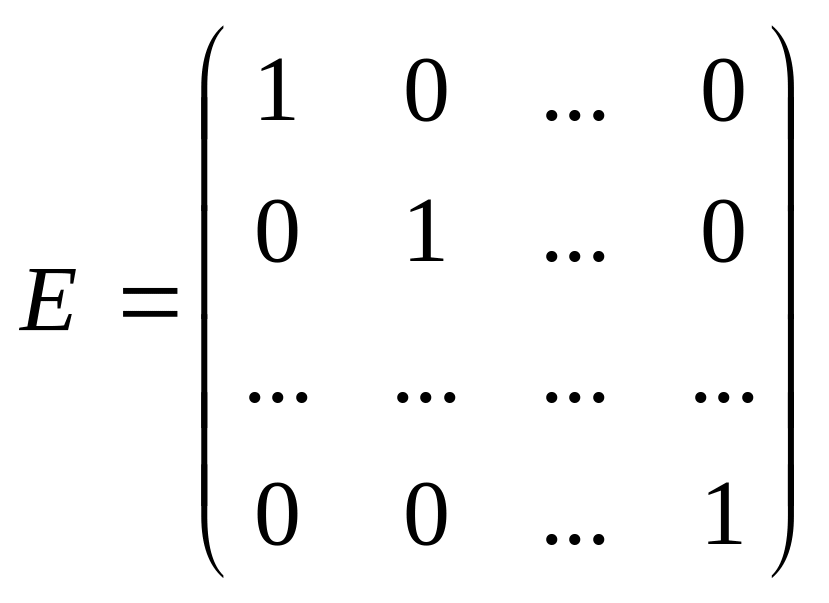 .Барлық
элементтері нолге тең матрица нолдік
матрица
деп аталады.
.Барлық
элементтері нолге тең матрица нолдік
матрица
деп аталады.
МАТРИЦАЛАРҒА ҚОЛДАНЫЛАТЫН АМАЛДАР
1.
Матрицаны санға көбейту.
Матрицаны
санға көбейту үшін оның барлық элементтерін
сол санға көбейту керек: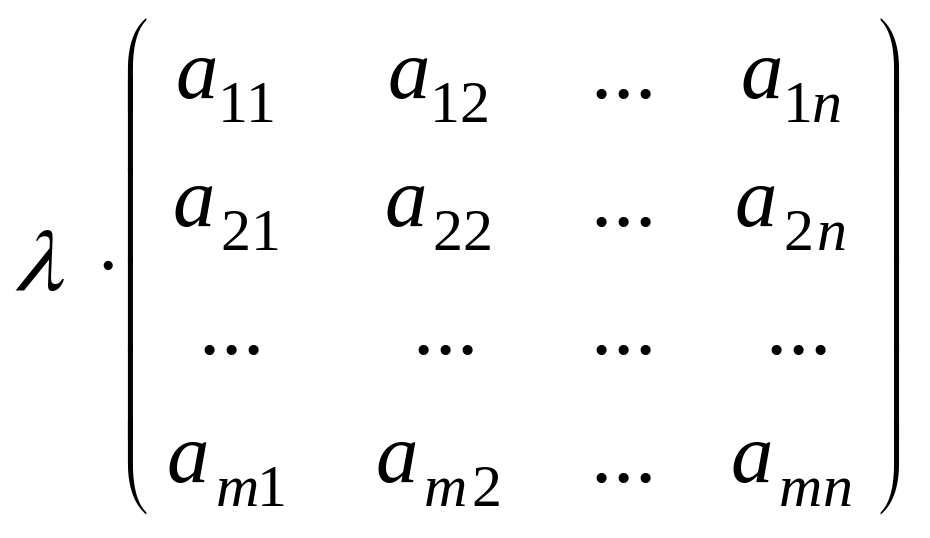
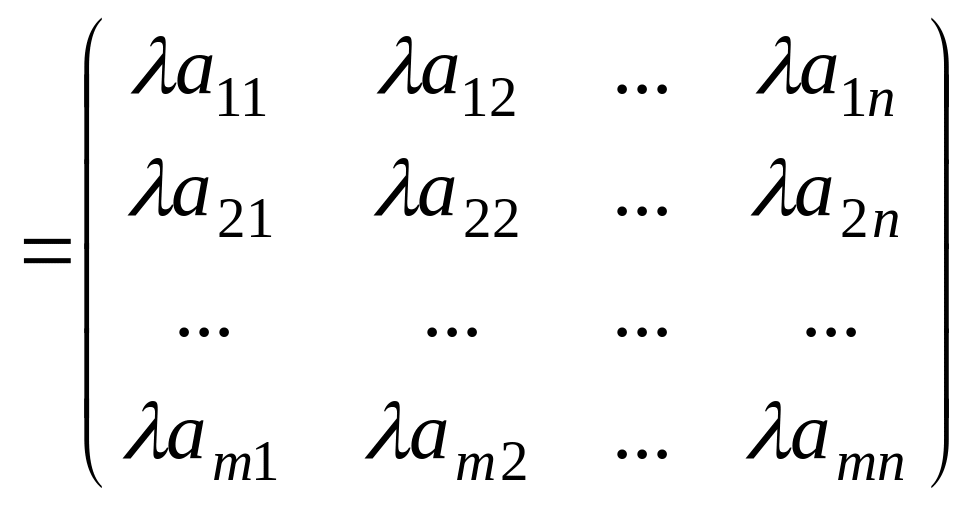
2.
Матрицаларды қосу және алу.
Өлшемдері
бірдей матрицаларды ғана қосуға болады.
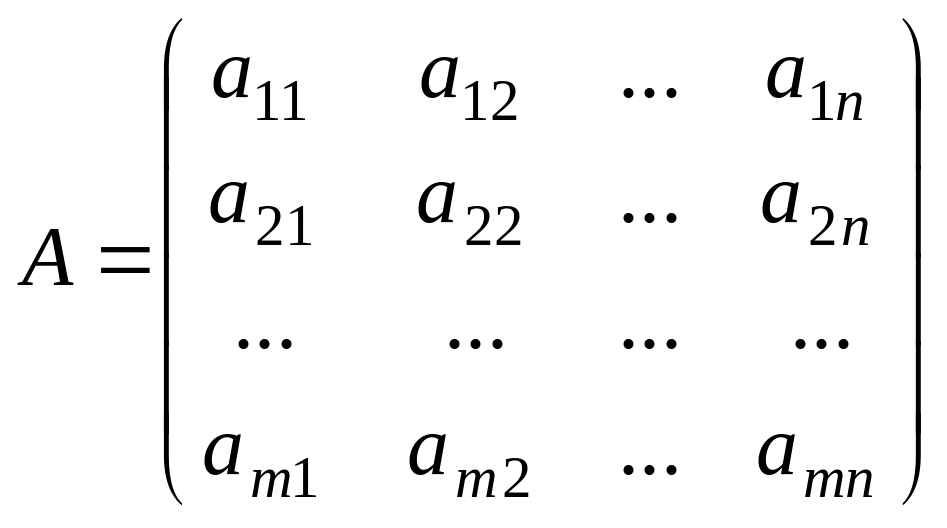 және
және
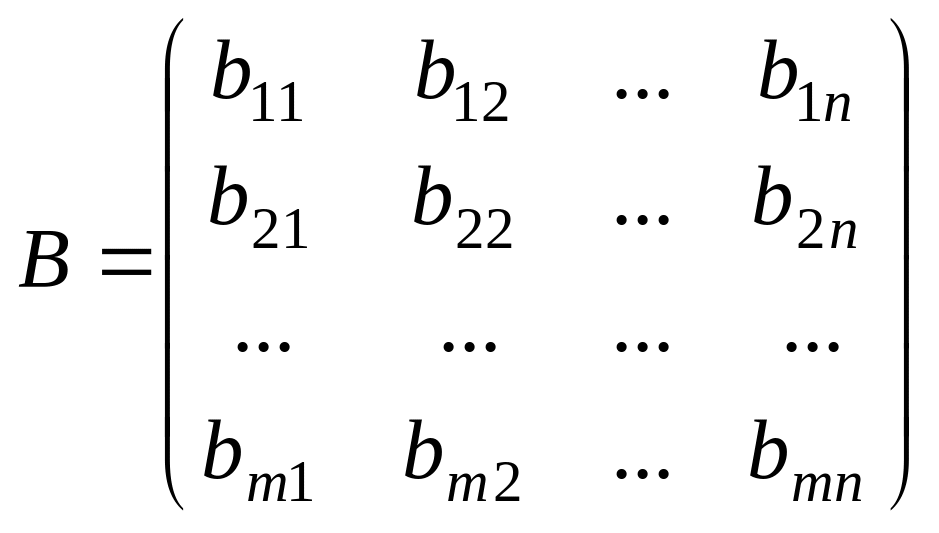 матрицаларының қосындысы деп элементтері
осы матрицалардың сәйкес элементтерінің
қосындысы болатын, А + В матрицаны
айтамыз:
матрицаларының қосындысы деп элементтері
осы матрицалардың сәйкес элементтерінің
қосындысы болатын, А + В матрицаны
айтамыз: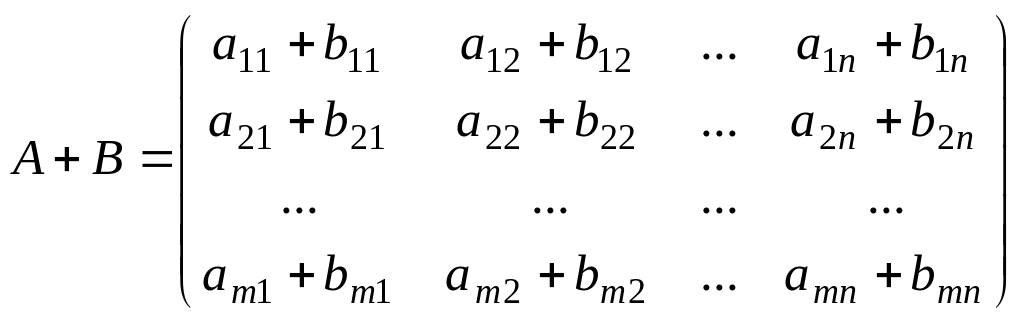
А матрицасынан В матрицасын алу үшін А матрицасына В матрицасын -1-ге көбейтіп қосу жеткілікті:
A – B = A+(-1)B
немесе А матрицасының әр элементінен В матрицасының сәйкес элементтері алынады.
3.
Матрицаларды көбейту. Бірінші
матрицаның тік жолдар саны мен екінші
матрицаның жатық жолдар саны тең болған
жағдайда ғана екі матрицаны көбейтуге
болады.
Өлшемі mxk
болатын А матрицасы мен өлшемі kxn
болатын В матриасы берілсін: Осы екі
матрицаны көбейткенде өлшемі mxn
болатын көбейтінді С матрица аламыз:![]() С
матрицасының
С
матрицасының
![]() элементі А
матрицаның
элементі А
матрицаның
![]() –жатық
жол элементтерін В
матрицаның
–жатық
жол элементтерін В
матрицаның
![]() –тік
жолының сәйкес элементтеріне көбейтіп
қосқанға тең болады:
–тік
жолының сәйкес элементтеріне көбейтіп
қосқанға тең болады:
![]() ,
,
![]() .
(1)
.
(1)
Қосу және көбейту амалдарының мынадай қасиеттері бар:
1. A+B=B+A |
|
2.(A+B)+C=A+(B+C) |
|
3. |
|
5) (A+B)C=AC+BC |
|
6. (AB)=( A)B=A(B) |
|
7) A(BC)=(AB)C |
|
Енді матрицаның өзіндік ерекшелігіне байланысты қасиеттерін қарастырайық.
8)
Біріншіден, екі матрицаның АВ
көбейтіндісі болғанмен ВА
көбейтіндісі болмауы мүмкін. Мысалы,
![]() көбейтіндісі
бар, бірақ
көбейтіндісі
бар, бірақ
![]() көбейтіндісі
жоқ, себебі бірінші матрицаның тік
жолдар саны екінші матрицаның жатық
жолдар санына тең емес;
көбейтіндісі
жоқ, себебі бірінші матрицаның тік
жолдар саны екінші матрицаның жатық
жолдар санына тең емес;
екіншіден, АВ және ВА көбейтінділері бар болғанмен, олардың өлшемдері әртүрлі болуы мүмкін.
9) А-квадрат матрица болса, онда мына теңдік орындалады: АЕ = ЕА = А.
4.
Матрицаны транспонерлеу.
Қандай да бір А
матрицасының жатық жолын сәйкес тік
жол етіп жазғаннан пайда болған матрицаны
берілген матрицаның транспонерленген
матрицасы
деп атайды да,
![]() деп белгілейді. Берілген матрицаның
өлшемі mxn
болса, оның транспонерленген матрицасының
өлшемі nxm
болады.
деп белгілейді. Берілген матрицаның
өлшемі mxn
болса, оның транспонерленген матрицасының
өлшемі nxm
болады.
2.
Квадрат матрица анықтауышы және олардың
қасиеттері.Квадрат
матрицаны сипаттауға қажетті анықтауыш
ұғымын енгізейік. Екінші
ретті матрицаның
![]() анықтауышы немесе екінші ретті анықтауыш
деп мынадай санды айтады:
анықтауышы немесе екінші ретті анықтауыш
деп мынадай санды айтады:![]() Мысалы,
Мысалы,
![]() матрицаның анықтауышын есептейік:
матрицаның анықтауышын есептейік:
![]() .
Ал үшінші ретті матрицаға
.
Ал үшінші ретті матрицаға
 үшінші ретті анықтауыш сәйкес келеді:
үшінші ретті анықтауыш сәйкес келеді:
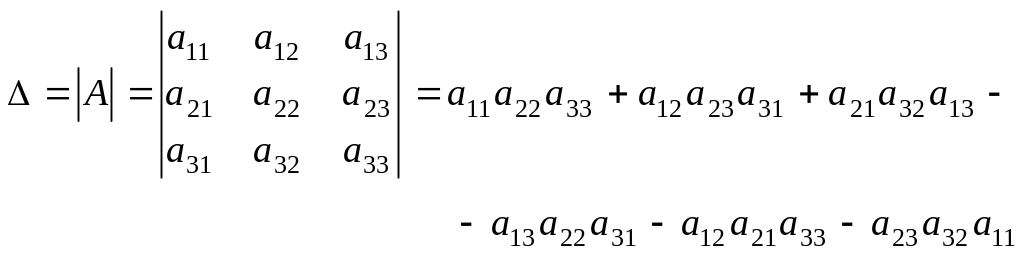 Бұл
анықтауыштың есептелуін үшбұрыш ережесі
немесе Саррус ережесімен оңай есте
сақтауға болады. Енді анықтауыш
қасиеттерін қарастырайық.1-қасиет.Анықтауыштың
жатық жолдарын сәкес тік жолдарымен
алмастырғаннан, яғни транспонерлегеннен,
анықтауыш мәні өзгермейді:
Бұл
анықтауыштың есептелуін үшбұрыш ережесі
немесе Саррус ережесімен оңай есте
сақтауға болады. Енді анықтауыш
қасиеттерін қарастырайық.1-қасиет.Анықтауыштың
жатық жолдарын сәкес тік жолдарымен
алмастырғаннан, яғни транспонерлегеннен,
анықтауыш мәні өзгермейді: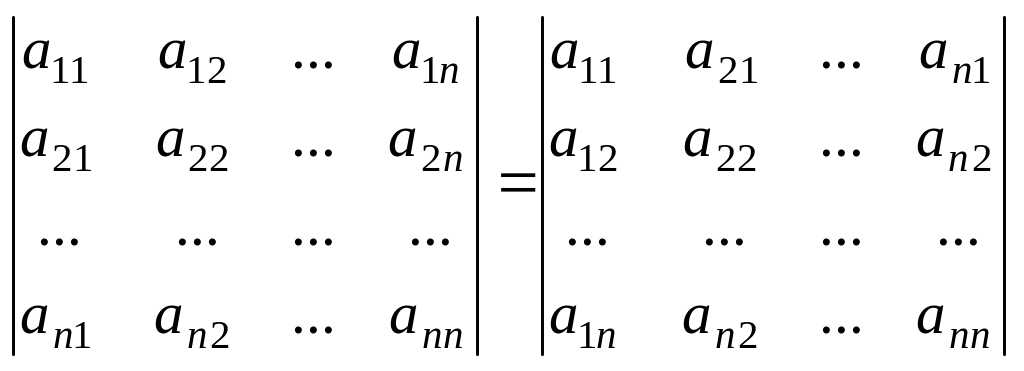 .
.
2-қасиет.Анықтауыштың
қандай да бір жолының ортақ көбейткішін
анықтауыш алдына шығаруға болады.
Үшінші ретті анықтауыштың екінші
жолындағы ортақ көбейткішті анықтауыш
алдына шығарамыз: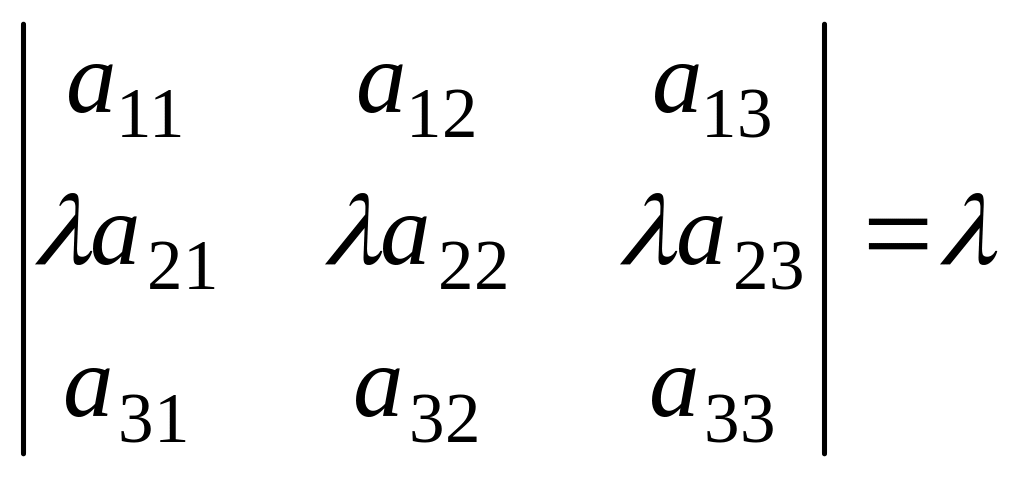
 .
.
3-қасиет.Анықтауыштың екі жолының орнын ауыстырғаннан анықтауыш таңбасы қарама-қарсы таңбаға өзгереді. Үшінші ретті анықтауыштың бірінші және екінші жолдарын алмастырайық:
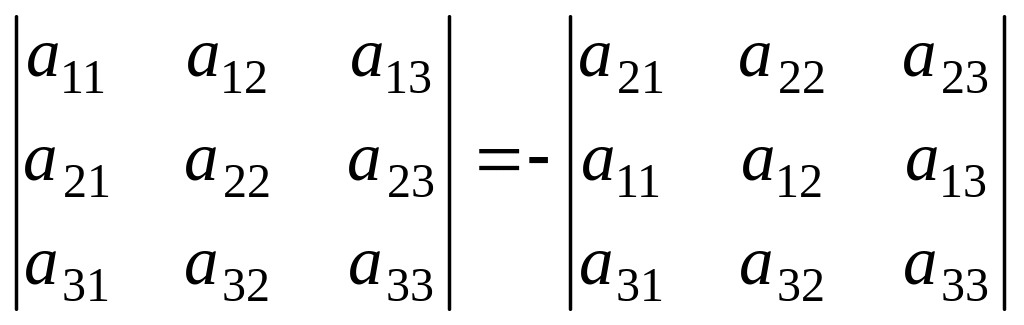
4-қасиет.
Егер
анықтауыштың екі жолы бірдей болса,
онда анықтауыш мәні нолге тең. Үшінші
ретті анықтауыштың бірінші және екінші
жолдары бірдей болсын: =0.
=0.
5-қасиет.Анықтауыштың бір жолын қандай да бір санға көбейтіп басқа жолға қосқаннан анықтауыш мәні өзгермейді. Үшінші ретті анықтауыштың бірінші жолын -ға көбейтіп екінші жолға қосайық:
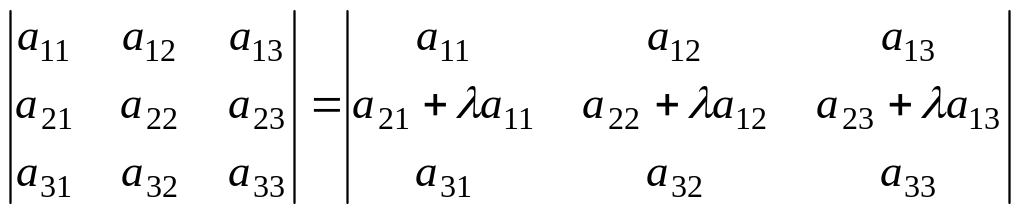 .
.
6-қасиет.Үшбұрышты
матрицаның анықтауышы диагональ
бойындағы элементтердің көбейтіндісіне
тең: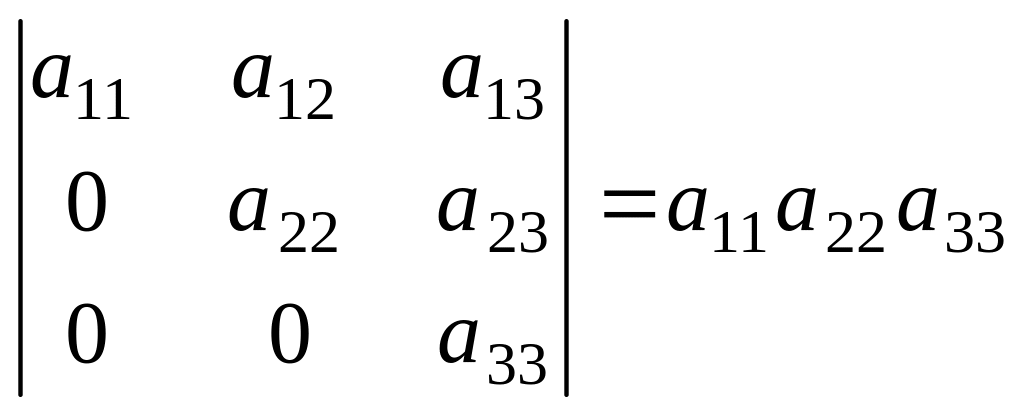 .
.
3.минор
және алгебралық толықтауыштар. Лаплас
теоремасыАнықтама.n-ретті
квадрат матрицаның
–жатық
жолы мен
–тік
жолын сызып тастағаннан кейін пайда
болған (n–1)-ретті анықтауықты
![]() элементінің миноры деп атайды және
элементінің миноры деп атайды және
![]() деп белгілейді.
элементінің
алгебралық толықтауышы деп мынадай
санды айтады:
деп белгілейді.
элементінің
алгебралық толықтауышы деп мынадай
санды айтады:![]() Үшінші
ретті марицаның
Үшінші
ретті марицаның
![]() элементінің алгебралық толықтауышы
мынадай сан:
элементінің алгебралық толықтауышы
мынадай сан:![]() Лаплас
теоремасы.
Лаплас
теоремасы.
![]()
![]() квадрат
матрицаның Δ анықтауышы оның кез келген
жол элементтерін сәйкес алгебралық
толықтауыштарға көбейтіп қосқанға
тең:
квадрат
матрицаның Δ анықтауышы оның кез келген
жол элементтерін сәйкес алгебралық
толықтауыштарға көбейтіп қосқанға
тең:![]() -
бұл анықтауыштың i–жатық
жолы бойынша жіктелініп есептелуі.
-
бұл анықтауыштың i–жатық
жолы бойынша жіктелініп есептелуі.
![]() -
бұл анықтауыштың j–тік
жолы бойынша жіктелініп есептелуі.
Алдыңғы мысалдағы
-
бұл анықтауыштың j–тік
жолы бойынша жіктелініп есептелуі.
Алдыңғы мысалдағы
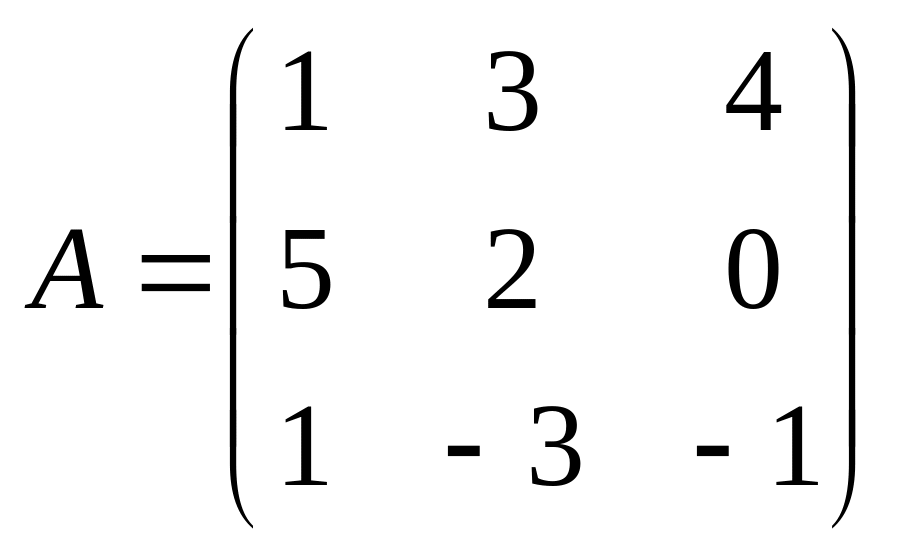 матрицасының анықтауышын бірінші жатық
жолы бойынша жіктеп есептейік:
матрицасының анықтауышын бірінші жатық
жолы бойынша жіктеп есептейік:
 ,мұндағы
алгебралық толықтауыштардың дайын
мәндерін алдыңғы мысалдан алдық.Лаплас
теоремасы n-ретті
анықтауыш есептеуді (n-1)-ретті
анықтауыш есептеуге келтіріледі.
,мұндағы
алгебралық толықтауыштардың дайын
мәндерін алдыңғы мысалдан алдық.Лаплас
теоремасы n-ретті
анықтауыш есептеуді (n-1)-ретті
анықтауыш есептеуге келтіріледі.
4.
Кері матрица, матрица
рангісі
квадрат матрица қарастырайық
Анықтама.Анықтауышы
нолге тең матрицаерекше,
ал нолге тең емес матрицаерекше
емес матрицадеп
аталады.
Кез келген
![]() сан үшін мына
сан үшін мына
![]() теңдігін қанағаттандыратындай кері
сан табылады. Квадрат матрица үшін де
осындай ұғым енгіземіз. Анықтама.А
квадрат
матрица үшін мына
теңдігін қанағаттандыратындай кері
сан табылады. Квадрат матрица үшін де
осындай ұғым енгіземіз. Анықтама.А
квадрат
матрица үшін мына![]() теңдікті
қанағаттандыратын
теңдікті
қанағаттандыратын
![]() матрица А
матрицаның
кері матрицасы деп
аталады.
Кері
матрицаны мына формуламен табады:
матрица А
матрицаның
кері матрицасы деп
аталады.
Кері
матрицаны мына формуламен табады:
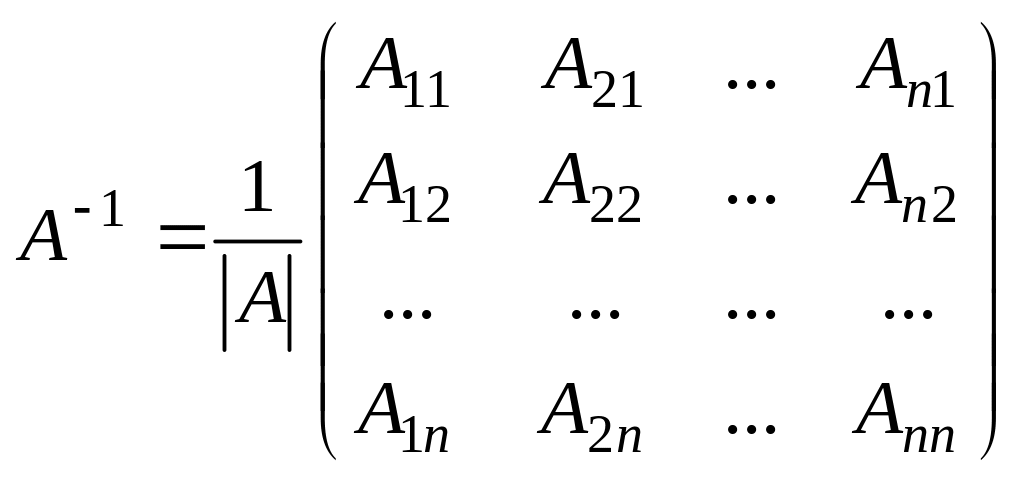 ,мұндағы
,мұндағы
![]() -матрица
анықтауышы, ал
-матрица
анықтауышы, ал
![]() -берілген
матрицаның
-берілген
матрицаның
![]() элементтерінің алгебралық толықтауыштары,
i=1,2,…,n;
j=1,2,…,n. Кез
келген квадрат матрицаның кері матрицасы
бола бермейді. Теорема(кері
матрица болуының қажетті және жеткілікті
шарты). Матрицаның
кері матрицасы болуы үшін ол ерекше
емес (
элементтерінің алгебралық толықтауыштары,
i=1,2,…,n;
j=1,2,…,n. Кез
келген квадрат матрицаның кері матрицасы
бола бермейді. Теорема(кері
матрица болуының қажетті және жеткілікті
шарты). Матрицаның
кері матрицасы болуы үшін ол ерекше
емес (![]() )
матрица болуы қажетті және жеткілікті.
)
матрица болуы қажетті және жеткілікті.
Берілген матрицаға кері матрицаны элементар түрлендірулер әдісімен де табуға болады. Бұл әдіс матрицаға элементар түрлендірулер қолдануға сүйенеді. Матрицаның элементар түрлендірулері деп мынадай түрлендірулерді айтамыз:
Матрицаны транспонерлеу;
Жолдардың орнын алмастыру;
Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейту;
Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейтіп басқа жолдың сәйкес элементтеріне қосу;
Барлық элементі ноль болатын жолды алып тастау.
матрица рангісін есептеуАнықтама. Матрицаның нолге тең емес минорларының ең үлкен реті матрица рангісі деп аталады:r=r(A)= rangA .Анықтамадан бірден мынадай тұжырымдар жасауға болады:
1.
![]() матрицасының
рангісі оның өлшемдерінің кішісінен
артпайды: r(A)
матрицасының
рангісі оның өлшемдерінің кішісінен
артпайды: r(A)![]() min(m,n).
2. Барлық элементтері ноль болғанда ғана
(нолдік матрица) матрица рангісі ноль
болады.3. n–ретті
квадрат матрица ерекше емес болғанда
матрица рангісі n–ге
тең болады .
min(m,n).
2. Барлық элементтері ноль болғанда ғана
(нолдік матрица) матрица рангісі ноль
болады.3. n–ретті
квадрат матрица ерекше емес болғанда
матрица рангісі n–ге
тең болады .
Мысал.
 матрицаның рангісін есептейік.
матрицаның рангісін есептейік.
Шешуі.
Матрица өлшемі 3х4
болғандықтан, оның рангісі 3-тен артпайды,
r(A)
min(3,4).
Егер үшінші ретті минорлардың ең
болмағанда біреуі нолден өзгеше болса,
онда матрица рангісі 3-ке тең болады.
Үшінші ретті минорлар матрицаның бір
тік жолын сызып тастағанда пайда
болады: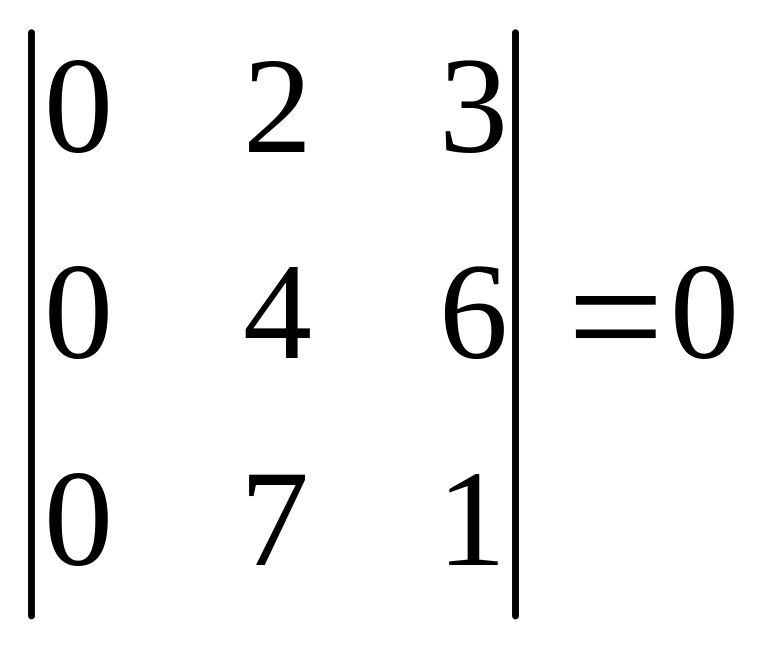 ,
,
 ,
,
 ,
,
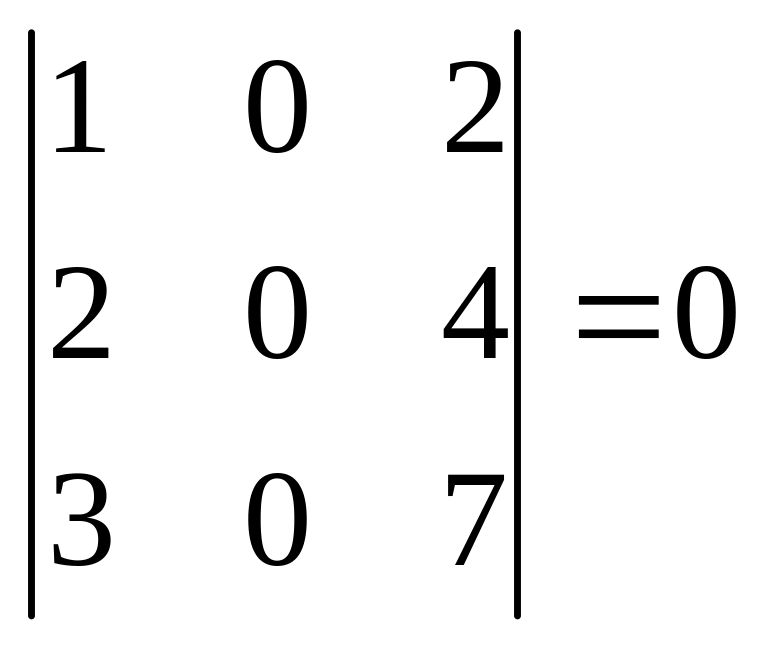 .
.
Үшінші
ретті минорлардың бәрі нолге тең
болғандықтан, ранг 3-ке тең бола алмайды.
Енді екінші ретті минорлардың ішінен
(олардың саны
![]() )
ең болмағанда бір нолге тең емес минор
тапсақ, матрица рангісі 2-ге тең болады.
Екінші ретті минорлар матрицаның бір
жатық, екі тік жолын сызып тастағанда
пайда болады. Айталық бірінші жатық жол
мен бірінші және екінші тік жолдарды
сызып тастағанда пайда болатын мына
минор:
)
ең болмағанда бір нолге тең емес минор
тапсақ, матрица рангісі 2-ге тең болады.
Екінші ретті минорлар матрицаның бір
жатық, екі тік жолын сызып тастағанда
пайда болады. Айталық бірінші жатық жол
мен бірінші және екінші тік жолдарды
сызып тастағанда пайда болатын мына
минор:
![]() ,
сондықтан r(A)=2.
Матрица өлшемі артқан сайын оның рангісін
барлық нолден өзге минорларды есептеу
жолымен анықтау қиындайды. Матрица
рангісін элементар түрлендірулер
әдісімен табу ондай қиындықтардан
құтқарады.Теорема.Элементар
түрлендірулер матрица рангісін
өзгертпейді.
Дәлелдеуі. Матрицаға элементар
түрлендірулер жүргізгенде оның анықтауышы
не өзгермей сақталады, не нолге тең емес
санға көбейтіледі. Яғни, оның реті
өзгермейді деген сөз. Олай болса, нолден
өзгеше минорлардың немесе матрица
рангісінің реті де өзгермейді. Осы
теореманы ескеріп, элементар түрлендірулер
жасап, берілген матрицаны барлық
диагоналдік элементтері нолден өзгеше
болатындай етіп сатылы түрге келтіреміз:
,
сондықтан r(A)=2.
Матрица өлшемі артқан сайын оның рангісін
барлық нолден өзге минорларды есептеу
жолымен анықтау қиындайды. Матрица
рангісін элементар түрлендірулер
әдісімен табу ондай қиындықтардан
құтқарады.Теорема.Элементар
түрлендірулер матрица рангісін
өзгертпейді.
Дәлелдеуі. Матрицаға элементар
түрлендірулер жүргізгенде оның анықтауышы
не өзгермей сақталады, не нолге тең емес
санға көбейтіледі. Яғни, оның реті
өзгермейді деген сөз. Олай болса, нолден
өзгеше минорлардың немесе матрица
рангісінің реті де өзгермейді. Осы
теореманы ескеріп, элементар түрлендірулер
жасап, берілген матрицаны барлық
диагоналдік элементтері нолден өзгеше
болатындай етіп сатылы түрге келтіреміз: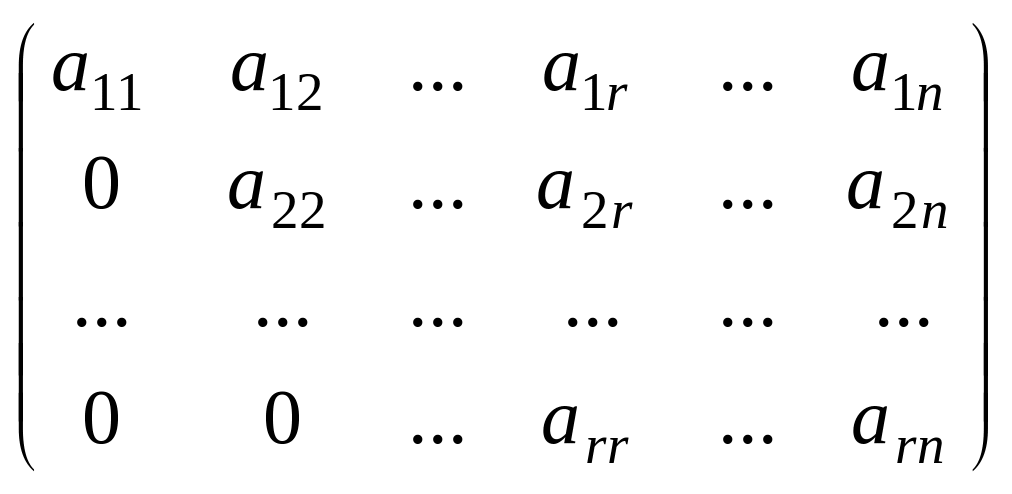 ,
мұндағы r
,
мұндағы r![]() п.
Осы
шарттың орындалуын матрицаны транстонерлеу
арқылы қамтамасыз етуге болады.Сонда
матрицаның r–ретті
нолден өзге миноры
п.
Осы
шарттың орындалуын матрицаны транстонерлеу
арқылы қамтамасыз етуге болады.Сонда
матрицаның r–ретті
нолден өзге миноры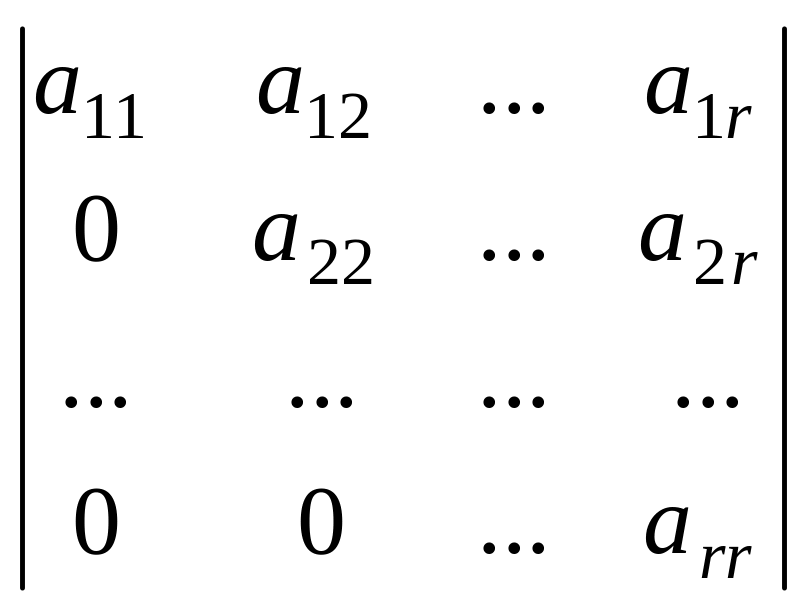 бар
болады да, матрица рангісі r-ге
тең болады, яғни r(A)=r.Мысал.
бар
болады да, матрица рангісі r-ге
тең болады, яғни r(A)=r.Мысал.
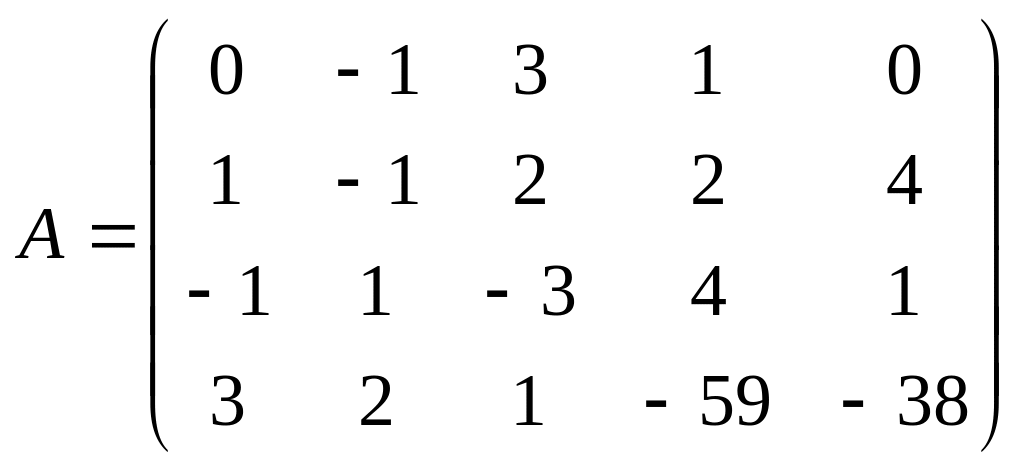 матрицасының рангісін есептейік.
матрицасының рангісін есептейік.
Шешуі. Элементар түрлендірулер көмегімен матрицаны сатылы түрге келтіреміз.
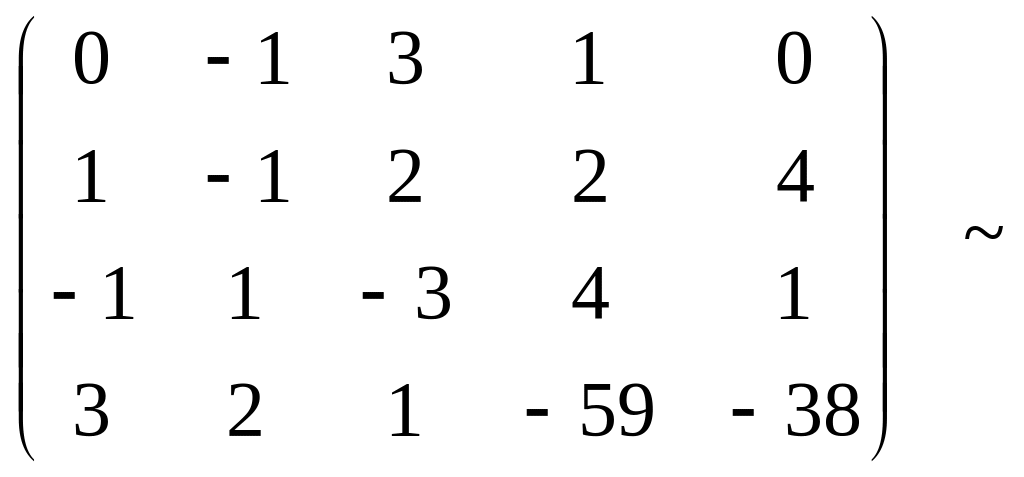



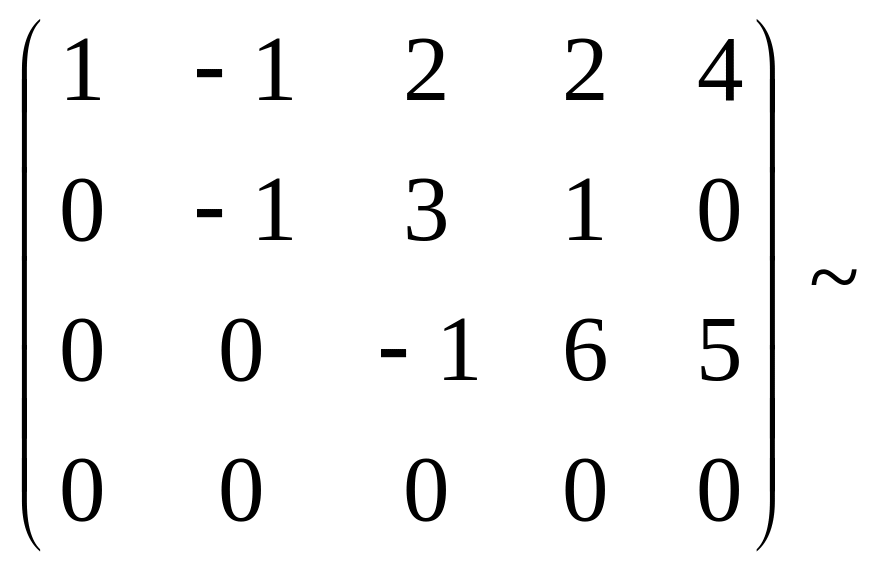
 .
.
Соңғы
матрица сатылы түрге келді және онда
нолге тең емес үшінші ретті минор бар
екенін бірден көруге болады:
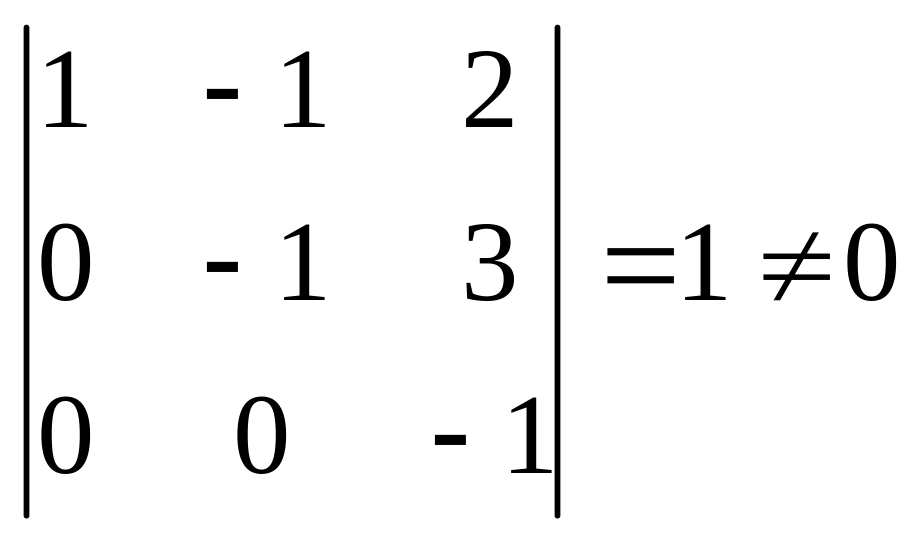 .
Сонымен матрица рангісі 3-ке тең, r(A)=3.
.
Сонымен матрица рангісі 3-ке тең, r(A)=3.
