1. Матрица дегеніміз не?

Оның түрлері қандай?

Матрицаға қолданылатын амалдарды жаз.

Анықтама. m жатық n тік жолдан құрылған кестені mxn өлшемді матрица деп атайды.

Матрицаны құрайтын сандар матрица элементтері деп аталады. Әдетте матрица латын алфавитінің бас әріптерімен, ал элементтері сәйкес кіші әріптермен белгіленеді:

Қысқаша жазылуы:

Бір ғана жатық жолдан құралған матрицаны жол-матрица, ал бір ғана тік жолдан құралған матрицаны бағана-матрица деп атайды:

- жол-матрица;

- бағана матрица.

Жол матрица мен бағана матрицаны кейде вектор деп те айта береді.

Жатық жолдар саны мен тік жолдар саны тең болатын матрица квадрат матрица деп аталады,

.

Квадрат матрицаның элементтері диагоналдық элементтер деп аталады да, матрицаның негізгі диагоналін құрайды. Ал элементтері қосымша диагоналдық элементтер деп аталады да, матрицаның қосымша диагоналін құрайды.

Квадрат матрицаның негізгі диагоналінің астындағы немесе үстіндегі элементтері нолге тең болса, матрица үшбұрышты матрица деп аталады,

,

Диагоналды емес элементтерінің бәрі нолге тең болатын квадрат матрица диагоналды матрица деп аталады,

.

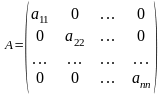Барлық диагоналды элементтері бірге тең болатын диагоналды матрица бірлік матрица деп аталады және оны Е әрпімен белгілейді,

.

Барлық элементтері нолге тең матрица нолдік матрица деп аталады.

Матрицалар және оларға амалдар қолдану.

2. Матрицаларды қосу және алу. Өлшемдері бірдей матрицаларды ғана қосуға болады. және матрицаларының қосындысы деп элементтері осы матрицалардың сәйкес элементтерінің қосындысы болатын, А + В матрицаны айтамыз

3. Матрицаларды көбейту. Бірінші матрицаның тік жолдар саны мен екінші матрицаның жатық жолдар саны тең болған жағдайда ғана екі матрицаны көбейтуге болады.

4. Матрицаны транспонерлеу. Қандай да бір А матрицасының жатық жолын сәйкес тік жол етіп жазғаннан пайда болған матрицаны берілген матрицаның транспонерленген матрицасы деп атайды да, деп белгілейді. Берілген матрицаның өлшемі mxn болса, оның транспонерленген матрицасының өлшемі nxm болады. Мысалы, матрицасының бірінші жатық жолын бірінші тік жол етіп, ал екінші жатық жолын екінші тік жол етіп жазып оның транспонерленген матрицасын аламыз

Қосу және көбейту амалдарының мынадай қасиеттері бар:

1) A+B=B+A	5) (A+B)C=AC+BC
2) (A+B)+C=A+(B+C)	6) (AB)=( A)B=A( B)
3) (A+B)= A+ B	7) A(BC)=(AB)C
4) A(B+C)=AB+AC

2. Екінші ретті квадрат матрица анықтауышы дегеніміз не?Үшінші ретті квадрат матрица анықтауышы дегеніміз не?Анықтауыштың қандай қасиеттерін білесің?

Екінші ретті матрицаның анықтауышы немесе екінші ретті анықтауыш деп мынадай санды айтады:

Ал үшінші ретті матрицаға үшінші ретті анықтауыш сәйкес келеді:

.

1-қасиет. Анықтауыштың жатық жолдарын сәкес тік жолдарымен алмастырғаннан, яғни транспонерлегеннен, анықтауыш мәні өзгермейді

2-қасиет. Анықтауыштың қандай да бір жолының ортақ көбейткішін анықтауыш алдына шығаруға болады. Үшінші ретті анықтауыштың екінші жолындағы ортақ көбейткішті анықтауыш алдына шығарамыз:

.

3-қасиет. Анықтауыштың екі жолының орнын ауыстырғаннан анықтауыш таңбасы қарама-қарсы таңбаға өзгереді.

4-қасиет. Егер анықтауыштың екі жолы бірдей болса, онда анықтауыш мәні нолге тең

5-қасиет. Анықтауыштың бір жолын қандай да бір санға көбейтіп басқа жолға қосқаннан анықтауыш мәні өзгермейді

6-қасиет. Үшбұрышты матрицаның анықтауышы диагональ бойындағы элементтердің көбейтіндісіне тең:

.

3. n-ретті квадрат матрица берілген. Осы матрицаның элементінің миноры дегеніміз не?

Осы матрицаның элементінің алгебралық толықтауышы дегеніміз не?

Лаплас теоремасын жаз.

n-ретті квадрат матрицаның –жатық жолы мен –тік жолын сызып тастағаннан кейін пайда болған (n–1)-ретті анықтауықты элементінің миноры деп атайды және деп белгілейді.

элементінің алгебралық толықтауышы деп мынадай санды айтады:

Үшінші ретті марицаның элементінің алгебралық толықтауышы мынадай сан:

Лаплас теоремасы. квадрат матрицаның Δ анықтауышы оның кез келген жол элементтерін сәйкес алгебралық толықтауыштарға көбейтіп қосқанға тең:

- бұл анықтауыштың i–жатық жолы бойынша жіктелініп есептелуі.

Мына анықтауыш есептеуде Лаплас теоремасын қолдан: .

4. n-ретті квадрат матрица берілген. Осы матрицаның кері матрицасы дегеніміз не?

Кері матрицаны алгебралық толықтауыштар арқылы қалай есептейді?

квадрат матрица қарастырайық.

Анықтама. Анықтауышы нолге тең матрица ерекше, ал нолге тең емес матрица ерекше емес матрица деп аталады.

А квадрат матрица үшін мына

теңдікті қанағаттандыратын матрица А матрицаның кері матрицасы деп аталады.

Кері матрицаны мына формуламен табады. ,мұндағы -матрица анықтауышы, ал -берілген матрицаның элементтерінің алгебралық толықтауыштары, i=1,2,…,n; j=1,2,…,n.

Кез келген квадрат матрицаның кері матрицасы бола бермейді.

Теорема(кері матрица болуының қажетті және жеткілікті шарты). Матрицаның кері матрицасы болуы үшін ол ерекше емес ( ) матрица болуы қажетті және жеткілікті.

Матрицаның элементар түрлендірулері деп мынадай түрлендірулерді айтамыз:

Матрицаны транспонерлеу;

5.n-ретті квадрат матрица берілген. Осы матрицаға жасалатын элементар түрлендірулер дегеніміз не?

Кері матрицаны элементар түрлендірулер әдісімен қалай табады?

1. Жолдардың орнын алмастыру;

2. Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейту;

3. Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейтіп басқа жолдың сәйкес элементтеріне қосу;

4)Барлық элементі ноль болатын жолды алып тастау

Енді кері матрица табу ережесіне көшейік: Берілген матрицаның оң жағына бірлік матрица жалғап жазу керек. Сонда өлшемді кеңейтілген матрица пайда болады. В матрицаға А матрицасының орнында бірлік матрица пайда болғанға дейін жатық жолдарына элементар түрлендірулер жасалады. Нәтижесінде бірлік матрицаның орнында кері матрица пайда болады.