17 Сұрақ. Матрицалар және олар,а амалдар қолдану

Матрица-математикада кез келген жиынның элементтерінен құрылған және m жол мен n бағаннантұратын тіктөртбұрышты  Атаблицасы. Матрицанытүзетін нысандар оның элементтері депаталады.

mxnөлшемді матрица немесе A= бұл жердегі i – матрица элементі қай бағанында, алj – қай қатарында орналасып тұрғанын көрсетеді.

2 x 3 өлшемді матрица. Осы жерде =0.7 және т.с.с.

Егер матрицада баған мен қатар саны бірдей болса, онда ол шаршы матрица болып табылады. -2-ші ретті шаршы матрица.

Егер матрицаның барлық элементтері 0-ге тең болса, онда ол нөлдік матрица деп аталады және оны 0-деп белгілей саламыз.

Матрицаның жоғарғы сол жақ бұрышынан төменгі оң жақ бұрышына дейінгі элементтер, матрицаның бас диагоналін құрайды. Мысалы:

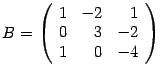  Осы матрицаның сандары матрицаның бас диагоналін құрайды.

Байқап тұрғанымыздай бас диагональдың элементтерінің индекстері(егер де әріп арқылы белгілесек) бірдей болады. . Ал n-ші ретті А шаршы матрицасының бас диагональдың элементтері , i=1,2,3,…,n.

Егер де бас диагональдың элементтерінен басқа, барлық элементтер 0-ге тең болса, онда сондай матрицаны диагональдік матрица д.а. Мысалы:

Б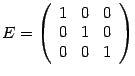 ас диагональдің элементтері 1-тең болатын диагональдік матрицаны бірлік матрица д.а. Е-деп белгілейміз.

• 3-ші ретті бірлік матрица

Бірлік матрицаның анықтамасынан көріп тұрғанымыздай, матрицаның элементтері 0-ге тең болады, егер элементтердің индекстері әртүрлі болса және 1-тең болады, егер индекстері бірдей болса. Математикада осындай қасиетке Кронекер символы ие ( ).

Екі матрица бір-біріне тең болады егер оның өлшемі де, сәйкес элементтері де бірдей болса.

Матрицаларға амалдар қолдану.Қосу

m x n өлшемді А және В матрицаларының қосындысы деп, жаңа тура сол өлшемді С матрицаны дейміз және , i=1,2,…,m; j=1,2,…,n. Қарапайым айтатын болсақ матрицаларды бір-біріне қосқанда олардың әрбір жол мен қатардағы элементтер қосылып, жаңа матрицаны құрайды. Мысалы:

Матрицаны санға көбейту

m x n өлшемді А матрицасының α санына көбейтіндісі деп, жаңа тура сол өлшемді С матрицасын айтамыз және , i=1,2,…,m; j=1,2,…,n. Қарапайым айтатын болсақ, матрицаның әрбір элементі сол α санына көбейтіледі де, жаңа С матрицасы пайда болады. Мысалы:

 

Матрицаларды азайту.

Жоғарғы көрсетілген 2 анықтамаға сүйене отырып,матрицалардың азайтындысын С=А+(-1)В=A-B түрінде жазсақ болады. Мысалы:

   ,  . 

Табайық 3А-2В:

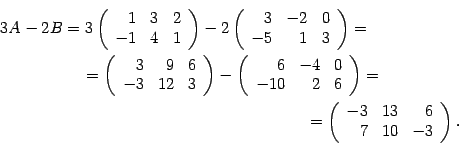
Матрицаларды көбейту.

m x n өлшемді А матрицасын, n x k өлшемді В матрицасына көбейткен кезде, жаңа С матрицасы пайда болады және оның элементтері келесі формула арқылы анықталады:

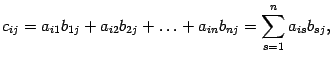
осы жердегі i=1,…,m j=1,…,k

Осы жерде назар аударылатын нәрселер:

1. Қай матрица бірінші, қай матрица екінші тұрғаны, себебі АВ≠ВА

2. 1-ші матрицаның баған саны 2-ші матрицаның жол санына тең болу керек, сонда тек сонда ғана олар бір-біріне көбейтіледі

3. Жаңа матрицаның жол саны 1-ші матрицаның жол санына тең, ал баған саны 2-ші м-ның баған санына тең болады.

Сонымен 2 м-ны көбейту алгоритмі: i-ншы жолда мен j-ншы қатарда тұрған (С матрицасында)элементті анықтау үшін, 1-нші матрицаның i-нші жолын алып, 2-нші матрицаның j-нші бағанын алып бір-біріне сәйкес элементтерін көбейтеміз(тура солай біз координаталар арқылы берілген 2 вектордың скаляр көбейтіндісін аламыз). Түсінікті болу үшін мысал келтірейік:

 

Жауабы сонымен:  

Матрицалардың көбейтіндісі келесі қасиеттерге ие:

1)

2) λ-сан

3)

4)  

5)      Е-бірлік матрица