9 Сұрақ. Көпмүшелікті екі мүшелікке бөлу. Горнер схемасы. Көпмүшелік түбірлері. Безу теоремасы.
Горнер схемасы.
көпмүшелігін
екі мүшелігіне бөлеміз. Қалдықпен бөлу
теоремасы бойынша
теңдігі орындалады, мұндағы
,
ал
.
Келесі
таблица
көпмүшелігінің коэффициенттері мен
қалдықты есептеудің тиімді әдісін
көрсетеді. Оны Горнер схемасы деп айтады.
|
|
|
... |
|
|
|
|
|
|
|
|
Көпмүшеліктің түбірлері.
Анықтама.
Егер
болса, онда
сақинасының
элементін
көпмүшелігінің түбірі дейміз.
Безу теоремасы.
Теорема. көпмүшелігі екі мүшелігіне бөліну үшін болуы қажетті және жеткілікті.
Теорема.
-
біртұтастық аймағы болатын сақинасындағы
дәрежелі
көпмүшелігінің
-дағы
түбірлерінің саны
нен
артпайды.
Көпмүшеліктің
түбірі. Горнер схемасы. Егер
мәнін f көпм-ң айнымалысына меншіктегенде
f(
)=0
болса
-тің
түбірі деп аталады.Әдетте әрбір
нөлдік көпм-ң түбірі болады.
1-теорема.(Безу теоремасы): -тің түбірі болуы үшін f көпмүшесі x- көпм-е қалдықсыз бөлінуі қажетті және жеткілікті.
Дәлелдеу.f(x)=(x-
)q(x)+f(
).Осыдан
f(
болуы үшін x-
қатыстың орындалуы қажетті және
жеткілікті.
2-теорема.Көпмүшелердің түбірлерін бөлу амалымен байланыстырады.Оның негізінде түбірдің еселігін енгізуге болады.
f
болсын. Егер
бірақ
көп-і f көп-н бөлмейтін болса,онда
түбірі k-еселі
түбір,ал
k саны
түбірдің еселігі
деп
аталады.Егер
түб-ң к еселігі 1-ге тең болса,онда
жай
түбір,ал
к
2
болғанда еселі
түбір
д.а. 0 нөлдік көпмүшесі үшін түбір еселік
ұғымы анықталмаған.Оның себебі айқын.
Кез
келген к натурал саны үшін
3-теорема.
еселіктері
сәйкес
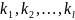болатын
нөлдік
емес
f–көп-ң
түбірлері
болсын.Онда
бір
g көп-і
үшін
f(x)=
және
g(
)
,
g(
)
Салдар.Нөлдік емес f көпмүшесінің түбірлерінің саны олардың еселігін қоса есептегенде f көпм-ің дәрежесінен аспайды.
Дәлелдеу.
P өріс
болғандықтан
degf=
қатыстарын
аламыз.
10 Сұрақ. Көпмүшелік түбірлерінің еселігі туралы теорема
Анықтама.
көпмүшелігі
ға
бөлініп, ал
бөлінбесе, онда
санын
көпмүшелігінің
өрісіндегі
еселі түбірі дейміз (мұндағы
бүтін
оң сан).
Теорема.
өрісіндегі
көпмүшелігіне
элементі
еселі түбірі болса, онда оның туындысына
еселі түбір болады.
Теорема.
өрісіндегі келтірімсіз
көпмүшелігі
көпмүшеліктің канондық жіктіліунде
дәрежемен енсе оның
туындысының канондық жіктеліуне
дәрежемен енеді.
11 Сұрақ. Берілген өрісте келтірілмейтін көпмүшеліктер. Комплекс сандар алгебрасының негізгі теоремасы(дәлелдеусіз) жәнеоның салдары.
Анықтама. өрісіндегі көпмүшелігі сол өрістегі дәрежеләрі өзінің дәрежесінен кіші нольдік көпмүшеліктерден өзгеше екі көпмүшеліктің көбейтіндісі түрінде жазылсакелтірімді, ал кері жағдайда келтірімсіз деп аталады.
Теорема. өрісіндегі дәрежесі 1-ден кем емес көпмүшелігі сол өрістегі саны шекті келтірімсіз көп мүшеліктердің көбейтіндісі түрінде бір ғана тәсілмен өрнектеледі
