36 Сұрақ. Түзудің нормаланған теңдеуі

37 Сұрақ. Екі түзудің өзара орналасуы.Нүктеден түзуге дейінгі қашықтық.

Түзулердің өзара орналасуы

Параллель түзулердің аттас проекциялары өзара параллель болады. Параллель түзулердің негізгі қасиеті: Берілген түзуден тыс жатқан нүкте арқылы осы түзуге паралель жалғыз ғана түзу жүргізуге болады. Егер түзу өзара параллель екі түзудің біреуін қиятын болса, онда ол екінші түзуді де қияды.

Қиылысушы түзулердің аттас проекциялары да өзара қиылысады және аттас проекциялардың қиылысу нүктелерін қосатын түзу вертикаль орналасады. Айқас түзулердің аттас проекцияларыең да қиылысуы мүмкін, бірақ аттас проекциялардың қиылысуы нүктелерін қосатын түзу вертикаль болмайды .

38 Сұрақ. Түзудің нормал және бағыттаушы векторлары арқылы түзудің арасындағы бұрыштың косинусын табу формулалары.

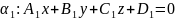,  ,   жазықтықтары берілсін. Онда осы жазықтықтардың арасындағы бұрыш ретінде, олардың  ,   , нормаль векторларының арасындағы бұрышты алуға болады. Демек Түзулер арасындағы бұрыш ретінде    және  бағыттауыш векторлары арасындағы бұрышты алуға болады: .

39 Сұрақ. Эллипс және оның элементтері.

Анықтама: Жазықтықтағы фокус деп аталатын екі нүктеден қашықтықтарының қосындысы әрқашанда тұрақты шама 2а-ға тең болатын нүктелердің гоеметриялық орнын эллипс дейді. және  эллипстің фокустары деп,   және   фокальдық радиустары деп аталады. Эллипстің теңдеуін қорытып шығару үшін жазықтықтың М(х,у) нүктесін аламыз да оның фокустан қашықтықтарының формуласын қарастырамыз: ; ; Эллипстің анықтамасы бойынша осы екі қашықтықтың қосындысы тұрақты және 2а-ға тең: ; Эллипстің теңдеуі математикалық жолмен құрылды, енді түрлендіру арқылы оны ықшамдаймыз: ; ; Енді ұқсас мүшелерін біріктіріп және 4-ке қысқарта отырып ықшамдаймыз: ; ; ; ; бұл өрнекті ға қысқартып ; 2a 2c; ;  (1). (1) - эллипстің канондық теңдеуін аламыз. Эллипстің абцисса осімен қиылысу нүктелерін табу үшін мына теңдеулер жүйесін шешеміз. OX:  Эллипстің ; екі төбесін аламыз.   эллипстің үлкен осі деп, ал а үлкен жарты осі деп аталады. Эллипстің ордината осімен қиылысу нүктелерін табу үшін мына теңдеулер жүйесін шешеміз. OY:   Сонда эллипстің қалған екі ;  төбесін аламыз. .     - эллипстің кіші осі деп, ал b кіші жарты осі деп аталады. Үлкен жарты осі мен кіші жарты осі тең болғанда шеңбердің канондық теңдеуі шығады. Анықтама: Фокустардың арақашықтығының фокальдық радиустардың қосындысына қатынасы  эллипстің эксцентриситеті деп аталады. Ординаталар осіне параллель және центрінен  қашықтықтағы екі түзу эллипс директрисасы деп аталады, былайша айтқанда фокальдық радиустың нүктеден директрисаға дейінгі қашықтыққа қатынасы тұрақты санға, яғни эксцентриситетке тең. Эллипстің жанамасының теңдеуі.   теңдеуін қарастырамыз. Қисыққа жүргізілген жанама  теңдеуімен табылатыны белгілі, эллипстің теңдеуінен туынды аламыз:  бұдан   k- ның мәнін жанама теңдеуіне қоямыз.  түрлендіріп ықшамдаймыз. ; . ; қа қысқартып ;  нүктесі эллипсте жатқандықтан оның координаталары эллипс теңдеуін қанағаттандырады, сондықтан оң жағы 1-ге тең. Сонымен эллипске жүргізілген жанаманың теңдеуі:   .