Счетчик со сквозным переносом.
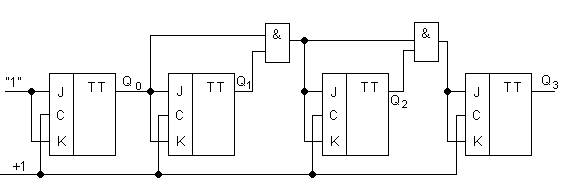
Параметры:
В
литературе данную схему часто называют
счетчик с последовательным переносом,
однако его параметры отличаются от
параметров счетчика с последовательным
переносом, ранее нами рассмотренным,
что проявляется если
.
Если же
,
то счетчики с последовательным и сквозным
переносом имеют близкие динамические
параметры.
Счетчик с комбинированным (или групповым) переносом.
Весь счетчик разбивается на группы. Внутри группы организуют параллельный перенос, между группами перенос сквозной либо последовательный.
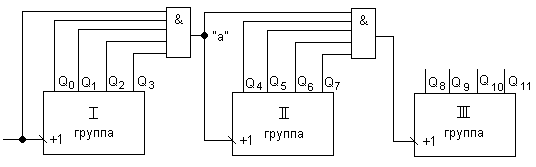
Предположим все 12 разрядов счетчика в 0, при поступлении первых импульсов работает только первая группа, т.к. среди Q0, Q1, Q2, Q3 есть хотя бы один 0 и сигнал А равен 0, пока счетчик досчитает до 14. Следующий спад после 14 переводит все разряды первой группы в 1, но к этому времени сигнал «+1» и сигнал А остается в 0. Появление импульса «+1» переведет А в 1, спад же «+1» сбросит все разряды первой группы и сбросит сигнал А. Спад сигнала А увеличит на единицу счетчик второй группы. В результате после числа 15 (01111) получим 16 (10000). Следующий импульс появится на 16-ом периоде «+1».
Если вместо элементов «И» на вход «+1» группы завести старший разряд предыдущей группы, то между группами получим последовательный перенос.
Реверсивные счетчики.
Существуют два способа построения реверсивных счетчиков:
Основанный на изменении межразрядных связей.
Основанный на обращении кодов.
Построение реверсивного счетчика способом изменения межразрядных связей.
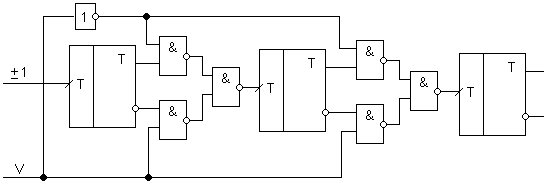
При
V=1 верхние конъюнкторы заблокированы.
Сигнал с инверсного выхода триггера
через два инвертора «И-НЕ» поступает
на вход Т, получаем схему суммирующего
счетчика с последовательным переносом.
При V=0
блокируются нижние конъюнкторы и прямой
выход триггера через два инвертора
«И-НЕ» поступает на вход Т, получаем
схему вычитающего счетчика с
последовательным переносом.
Построение реверсивного счетчика способом обращения кода.
Прямые значения Инверсные значения
с триггеров с триггеров
Если прямые значения выходов разрядов увеличивается на 1, то их инверсии уменьшаются на 1, следовательно, при выдаче прямого значения разрядов получаем суммирование, а при выдаче инверсного – вычитание. Однако, если в момент смены направления счета, вместо прямого значения выдать инверсное, или наоборот, то момент смены приведет к изменения значения на выходе. Чтобы этого не произошло надо произвести двойную инверсию: 1 – инвертировать содержимое счетчика и 2 – выдать инверсное значение.
Данный способ удобен лишь в том случае, если в счетчике имеются обе микрооперации.
Счетчики с произвольным модулем счета (или не двоичные).
Не двоичные счетчики – это счетчики, у которых M≠2n, где n – число разрядов, а М – число состояний.
Существует два подхода к реализации таких счетчиков:
За основу берут сразу не двоичный счетчик.
За основу берут двоичный счетчик и удаляют лишние состояния.
К не двоичным счетчикам относят: полиноминальные, счетчики Джонсона и др.
Из двоичных счетчиков не двоичные получают методом блокировки переноса или методом принудительного насчета.
Рассмотрим не двоичные счетчики на примере двоично-десятичного счетчика (модуль счета 10).
В двоично-десятичном коде одна десятичная цифра представлена четырьмя двоичными разрядами. Эти четыре разряда называют тетрадой или декадой.
Цифра |
Тетрада |
|
|||
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
2 |
0 |
0 |
1 |
0 |
|
3 |
0 |
0 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
|
5 |
0 |
1 |
0 |
1 |
|
6 |
0 |
1 |
1 |
0 |
|
7 |
0 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
|
9 |
1 |
0 |
0 |
1 |
|
|
1 |
0 |
1 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
|
|
1 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
|
запрещенные
За основу берут сразу не двоичный счетчик.
Полиноминальные счетчики.
Полиноминальными счетчиками называют пересчетные схемы, получаемые на основе сдвигающих регистров, в которые заведены обратные связи через сумматоры по модулю 2. Часто используют для получения псевдослучайной последовательности чисел.
Сумматор по модулю 2:
x1 |
x2 |
y |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Условное графическое обозначение:
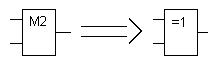
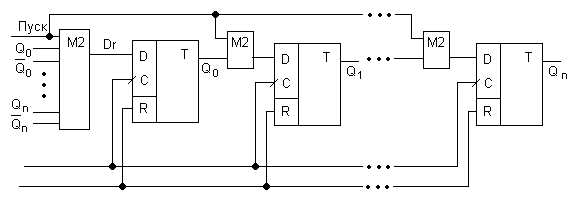
Двухвходовые сумматоры на входе D используются лишь в начальный момент для установки начального кода. На вход триггера Q0 устанавливается многовходовой сумматор, на вход которого заводят прямые или инверсные выходы триггеров. Количество разрядов которые заводят на вход М2 не регламентируются (может быть 1, а может и n+1). Если на вход М2 заводятся только прямые значения Q или четное количество инверсных, то счетчику обязательно требуется сигнал «Пуск». Если число инверсных входов не четно, то сигнал «Пуск» не обязателен, а тогда не нужны и двухвходовые сумматоры по модулю 2.
Многовходовой сумматор дополнительно может быть установлен и на входы других разрядов, не только Q0. В стандартном полиноминальном счетчике на вход многовходового сумматора М2 заводят только прямые значения Q и начальная установка такого счетчика состоит из двух этапов:
В начале подают сигнал R, который сбрасывает все триггера и счетчик получает значение 0000. В этом состоянии он может находиться сколь угодно долго.
Далее на один такт сигнала С подается сигнал «Пуск». И в те разряды, куда заведен сигнал «Пуск» вдвинется 1. Во время работы сигнал «Пуск» равен 0. При этом получаем обычный сдвиговый регистр, только на вход Dr заведена сумма разрядов.
Пример: Стандартный счетчик на 7 состояний.
Q2 |
Q1 |
Q0 |
D1 |
Пуск |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1
повтор |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
М=7 (модуль счета)
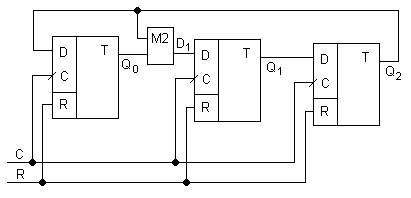
Q2 |
Q1 |
Q0 |
D1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
М=7 (модуль счета)
Если полиноминальный счетчик имеет 2n-1 состояний и одно состояние – начальное устойчивое, то его называют генератор псевдослучайной последовательности.
Счетчики Джонсона
Код Джонсона.
|
Q3 |
Q2 |
Q1 |
Q0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
1 |
1 |
3 |
0 |
1 |
1 |
1 |
4 |
1 |
1 |
1 |
1 |
5 |
1 |
1 |
1 |
0 |
6 |
1 |
1 |
0 |
0 |
7 |
1 |
0 |
0 |
0 |
Каждое состояние кода Джонсона однозначно определяется по двум разрядам, следовательно, чтобы иметь дешифратор Джонсона на 2n выходов необходимо воспользоваться n двухвходовыми элементами. Два соседних состояния кода Джонсона разнятся лишь в одном разряде, следовательно, при работе счетчика всегда переключается только один разряд. И только один разряд может внести помеху из-за переключения и потребляет динамическую мощность. В виду последнего счетчик в коде Джонсона можно строить на неограниченное число разрядов. При наличии n триггеров получаем 2n состояний – четное число. Если необходимо получить нечетное число состояний удаляется состояние содержащее все 1.
Схемотехнически счетчик Джонсона представляет собой сдвигающий регистр с перекрестной обратной связью.
2*4=8 состояний (4 – число триггеров)
Схема на нечетное количество состояний:
Q3 |
Q2 |
Q1 |
Q0 |
Dr |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
Счетчик не обладает самовосстанавливаемостью, если он попадет в любое запрещенное состояние, то он из него не выйдет.
Q3 |
Q2 |
Q1 |
Q0 |
Dr |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
Счетчик Джонсона с самовосстановлением.
Q3 |
Q2 |
Q1 |
Q0 |
Dr |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
Q1 |
|
|
|
|
|
Q0 |
|
|
1 |
1 |
1 |
* |
|
|
* |
* |
1 |
* |
|
|
0 |
* |
0 |
0 |
Q3 |
Q2 |
0 |
* |
* |
* |
Введем второе покрытие, надеясь, что оно обеспечит само восстановление.
Q3 |
Q2 |
Q1 |
Q0 |
Dr* |
|
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
|
Если в цикле запрещенных состояний изменить 0 на 1 напротив кода 1001, то из любого запрещенного состояния, по крайней мере, через 8 тактов счетчик вернется в разрешенное. Для упрощения схемы можно так же поменять 0 на 1 напротив комбинации 1011.
Для счетчика Джонсона существует обобщенная формула:
Например:
Для упрощения схемы коррекции её можно распределить между разрядами регистра.
Пример счетчика:
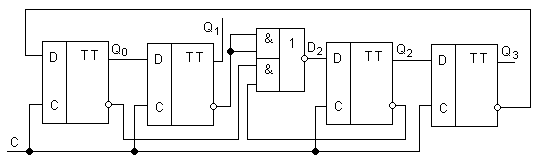
Счетчик Джонсона Счетчик Джонсона
без самовосстановления: с самовосстановлением:
Q3 |
Q2 |
Q1 |
Q0 |
D2 |
D2* |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
Иной подход к восстанавливаемости работоспособности счетчика Джонсона.
В любой запрещенной комбинации встречаются 0 и 1, следовательно, после какого-либо количества сдвигов мы получим в старших разрядах 10. При этом среди разрешенных комбинаций 10 в старших разрядах имеет лишь состояние 1000…00, следовательно, выявив 10 в старших разрядах можно младшие разряды сбросить, на этом и строится принцип коррекции.
Если Q4=1 и Q3=0, то на выходе элемента «ИЛИ-НЕ» - 1, и она сбрасывает содержимое регистра. Получаем разрешенную комбинацию 1000…0.
Удаление лишних состояний из двоичного счетчика.
За основу берут двоичный счетчик и удаляют лишние состояния.
В данном методе путем блокировки переносов в двоичном счетчике добиваются заданного модуля счета. Это осуществляется путем формального синтеза, имеющего следующие этапы:
Приводятся таблицы переходов и функции возбуждения.
Осуществляется тем или иным образом минимизация функции возбуждения (например, с помощью карт Карно).
Строится схема.
Если при минимизации получают КНФ или ДНФ, то полученный счетчик будем иметь с параллельным переносом. Если при получении функции возбуждения старших разрядов используют значение функции младших разрядов, то получают схему со сквозным переносом.
Пример: Двоично-десятичный счетчик на JK-триггерах.
Таблица переходов |
|
Функция возбуждения |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q3 |
Q2 |
Q1 |
Q0 |
|
Q3 |
Q2 |
Q1 |
Q0 |
|
J3 |
K3 |
|
J2 |
K2 |
|
J1 |
K1 |
|
J0 |
K0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
|
0 |
* |
|
0 |
* |
|
0 |
* |
|
1 |
* |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
* |
|
0 |
* |
|
1 |
* |
|
* |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
* |
|
0 |
* |
|
1 |
* |
|
1 |
* |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
... |
... |
|
... |
... |
|
... |
... |
|
... |
... |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
|
... |
... |
|
... |
... |
|
... |
... |
|
... |
... |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
... |
... |
|
... |
... |
|
... |
... |
|
... |
... |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
|
... |
... |
|
... |
... |
|
... |
... |
|
... |
... |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
... |
... |
|
... |
... |
|
... |
... |
|
... |
... |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
|
... |
... |
|
... |
... |
|
... |
... |
|
... |
... |
1 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
|
* |
1 |
|
0 |
* |
|
0 |
* |
|
* |
1 |
После таблицы минимизируем, например, с помощью карт Карно, и получаем следующий результат:
Сигнал
блокирует распространение переноса от
Q0
к Q1,
в остальном схема подобна двоичному
счетчику с параллельным переносом. От
0000 до кода 0111 счетчик считает как обычный
двоичный, т.к.
=1.
В состоянии 0111 на J
и K
всех триггеров – 1, и все они перейдут
в противоположное состояние, т.е. в 1000.
станет равно 0 и заблокирует перенос из
Q0
в Q1,
следующий импульс переведет счетчик в
состояние 1001. Блокировка переноса
сохраняется, а на К входе триггера Q3
- 1, следовательно, по следующему импульсу
все триггеры окажутся в 0.
В заключении необходимо проверить поведение счетчика в запрещенных комбинациях:
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
Счетчик из всех запрещенных комбинаций выходит в разрешенные, т.е. обладает самовосстанавливаемостью.
Счетчики с принудительным насчетом.
M=2n-L
Для получения счетчика с модулем счета М необходимо удалить L состояний.
В таких счетчиках, когда двоичный счетчик доходит до последнего разрешенного состояния (или первого запрещенного), то с помощью установочных входов триггера счетчик переводят на L состояний больше, а дальше он продолжает считать как обычный двоичный.
Двоично-десятичный счетчик:
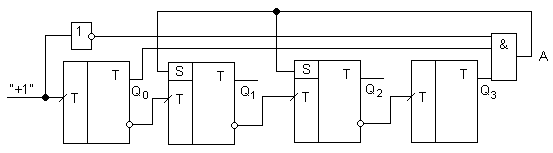
Счетчик считает как обычный двоичный счетчик с последовательным переносом от 0 до 9, т.к. при этом сигнал А=0. В состоянии 9 Q3 и Q0 равны 1, а значит на двух входах элемента «И» - 1. Как только инверсия сигнала «+1» станет равной 1, т.е. «+1» перейдет в 0, А станет равный 1 и установит триггеры Q1 и Q2 через установочные входы S в 1. Счетчик окажется в состоянии все 1. Следующим импульсом «+1» счетчик естественным образом будет переведен во все 0.
Схема имеет модуль счета равным 10, однако последнее состояние имеет два кода – 9 и15, что является недостатком.
Установочные входы триггера всегда имеют высший приоритет, чем прочие. Так если у триггера S=1 и появится фронт на входе Т, то 1 на входе S удержит триггер в 1. Такая ситуация может возникнуть при переходе счетчика от 1111 к 0000, чтобы этого не произошло должно выполнятся следующее неравенство:
tз.не+tз.&<tз.Tr
где представлены задержки элементов «НЕ», «И» и триггера.
Частным случаем счетчика с принудительным насчетом является счетчик с управляемым сбросом. В таком счетчике, пропустив L состояний, схема оказывается в состоянии все 0.
Двоично-десятичный счетчик:
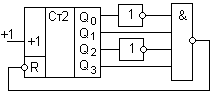
Первое запрещенное состояние это 10 (1010), как только оно появляется, схемой формируется сигнал сброса, и счетчик оказывается в состоянии все 0.
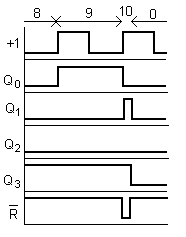
Т.к. при счете схемы 1 в Q3 и Q1 встречаются один раз, состояние 1010 можно выделить по двум единицам и не использовать инверторы.
В данной схеме также возникают гонки, т.к. исчезновение хотя бы одного сигнала Q3 или Q1 убирает сигнал «Reset», а времена сброса Q1 и Q3 могут быть разными.