§ 1.4Вопросы для самопроверки и задачи к §1.1 и 1.2

1.4.1Вопросы для самопроверки

1. Перечислите основные свойства алгоритмов.

2. Опишите условия, которым должны удовлетворять исполнители алгоритмов.

3. Какие из приведенных ниже последовательностей действий можно отнести к алгоритмам, а какие нельзя. Объясните почему?

   • Инструкция, направленная из разведцентра резиденту с указанием порядка встречи с прибывающим к нему на явку агентом.

   • Напечатанная на пакете инструкция по приготовлению супа из концентрата.

   • Программа для вычисления n!, написанная на одном из языков программирования.

4. Дайте определение вычислимой функции.

5. Чем частичная функция отличается от тотальной? приведите примеры.

6. Дайте определение разрешимого множества. Приведите примеры.

7. Дайте определение перечислимого множества. приведите примеры.

8. Что такое характеристическая функция множества?

9. При каком условии перечислимое множество является также разрешимым?

1.4.2Задачи к §1.1 и 1.2

Составьте алгоритмы вычисления следующих функций. (За образец оформления возьмите решение примеров 1.2.4 и 1.2.5)

1. Функция следования в двоичной системе счисления. (Указание: если последняя цифра числа равна 0, то ее нужно увеличить на 1 и остановить процесс, если последняя цифра 1, то ее заменяют на 0 и переходят на одну цифру влево. Чтобы этот процесс работал корректно, удобно вначале приписать к входному числу слева цифру 0. Если она не была использована, то по окончании работы алгоритма ее нужно стереть.)

2. Функция следования в десятичной системе счисления. (Смотри указание к задаче 1.)

3. Характеристическая функция множества четных чисел. (Указание: если последняя цифра числа четна, то характеристическая функция равна 1, иначе – 0.)

4. Характеристическая функция чисел, делящихся на 5. (Кодировка – десятичная.)

5. Функция в унарной кодировке.

6. Функция в двоичной кодировке.

7. Функция в десятичной кодировке.

8. Функция (По аналогии с примером 1.2.5.)

Составьте алгоритмы распознавания следующих множеств:

9. Множество чисел, кратных 10.

10. Множество простых чисел.

11. Множество троек чисел , таких, что .

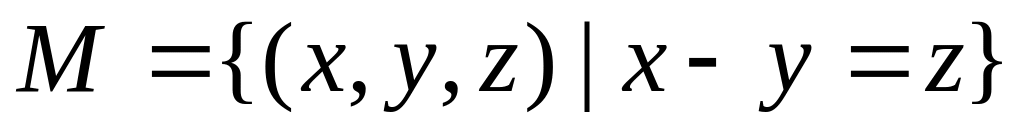12. Множество чисел, являющихся кубами некоторых натуральных чисел.

Укажите функции, порождающие следующие множества (докажите, что следующие множества перечислимы):

13. Множество натуральных чисел, которые при делении на m в остатке дают число r (r<m).

14. Множество натуральных чисел, которые являются разностями квадратов двух натуральных чисел.

15. Множество натуральных чисел, которые являются суммами кубов двух натуральных чисел.

§ 1.5Исчисления алгоритмов

1.5.1Необходимость исчислений

В предыдущих примерах мы использовали различные способы записи алгоритмов, особо не вдаваясь в описание свойств исполнителя, правил останова и другие тонкости. Для более детально и тщательного исследования свойств алгоритмов (вычислимых функций), нам необходимо давать детальное описание всех действий алгоритма, используя для этого специальный язык (исчисление). При этом возникает серьезная проблема:

Нужно показать, что с помощью данного языка (исчисления) можно записать алгоритм любой алгоритмически разрешимой задачи.

По аналогии с математической логикой, такое свойство исчислений будем называть полнотой.

На настоящее время ни для одного исчисления алгоритмов на прямую не доказано свойство полноты. С другой стороны, есть возможность качественного подтверждения этого факта.

Опять же в курсе математической логики рассматриваются различные модели некоторой аксиоматической теории и разрешение вопроса о полноте этой аксиоматической теории сводится к доказательству изоморфности всех ее моделей.

Мы поступим с исчислениями алгоритмов следующим образом. Рассмотрим большое количество примеров исчислений и покажем их изоморфность. Такой подход даст нам право предполагать, что все рассмотренные исчисления являются полными (обобщенный тезис Тьюринга).

В предположении о полноте исчислений алгоритмов мы, во второй главе, продолжим изучение свойств вычислимых функций.