1. Зведення багатокритеріальної задачі до однокритеріальної

Розглянемо найбільш вживані способи розв’язку багатокритеріальних задач. Перший спосіб полягає у тому, щоби багатокритеріальну задачу звести до однокритеріальної. Це означає введення суперкритерію, тобто скалярної функції векторного аргументу:

q₀(x) = q₀(q₁ (x),q₂(x),…,q_p(x)). (2)

Суперкритерій дозволяє впорядкувати альтернативи за величиною q₀, виділивши найкращу альтернативу (у смислі цього критерію). Вид функції q₀ визначається тим, як представляється внесок кожного критерію у суперкритерій. Звичайно використовують адитивні або мультиплікативні функції:

q₀ = ; (3)

1 - q₀ = (4)

Коефіцієнти s_i забезпечують, по-перше, безрозмірність числа q_i/s_i (часткові критерії можуть мати різну розмірність, і тоді деякі арифметичні операції над ними, наприклад додавання, не мають смислу) і, по-друге, у необхідних випадках (як у формулі (4)) виконання умови β_i q_i/s_i ≤ 1. Коефіцієнти α_i та β_i виражають відносний внесок часткових критеріїв у суперкритерій.

При даному способі задача зводиться до максимізації суперкритерію:

x^*= arg q₀(q₁ (x),q₂ (x),…,q_p (x)). (5)

Очевидне достоїнство об’єднання декількох критеріїв в один суперкритерій супроводжується рядом трудностей та недоліків, котрі необхідно враховувати. Залишивши осторонь труднощі побудови самої функції та обчислювальні труднощі її максимізації, звернемо увагу на наступний дуже важливий момент. Впорядкування точок у багатовимірному просторі у принципі не може бути однозначним та повністю визначається видом функції упорядкування. Суперкритерій грає роль цієї функції упорядкування, і його навіть „невелика” зміна може привести до того, що оптимальна у новому розумінні альтернатива з’явиться дуже сильно відмінною від старої. На Рис.17 а) видно, як змінюється вибір найкращої альтернативи при простій зміні коефіцієнтів лінійної функції упорядкування (3), що відображається в зміні нахилу відповідної прямої: q₀₁(x₁^*) > q₀₁(x₂^*), але q₀₂(x₁^*) < q₀₂(x₂^*). Відмітимо, що лінійні комбінації часткових критеріїв придають впорядковуванню наступний зміст: „Чим далі від нуля у заданому напрямку, тим краще”. На Рис.19 а) напрямки, що відповідають суперкритеріям q₀₁ та q₀₂, зображені стрілками. Другий варіант пошуку альтернативи, що найбільш віддалена від нуля у заданому напрямку, максимізує мінімальний критерій:

x^* = arg 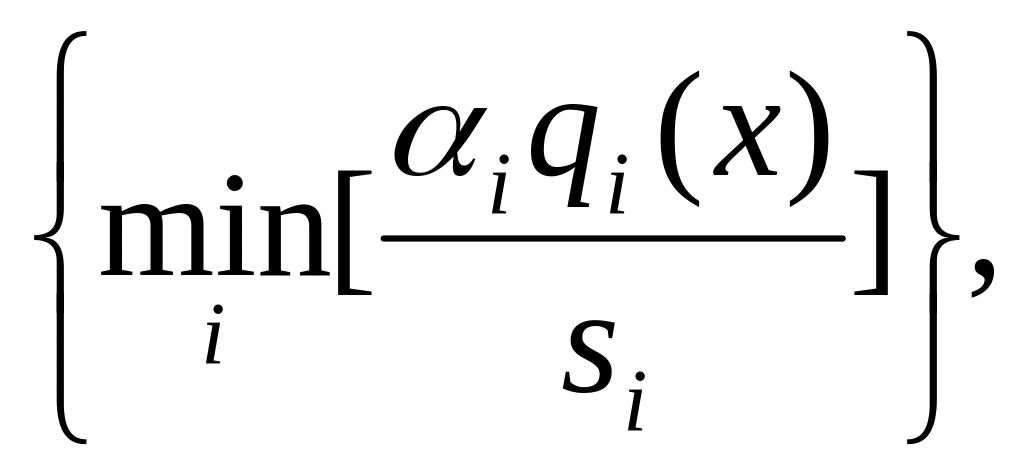(6)

що означає пошук навколо напрямку α_iβ_i/s_i = Сonst методом „підтягування самого відстаючого”.

2. Умовна максимізація

Недоліки згортки декількох критеріїв заставляють шукати інші підходи до розв’язку задач багатокритеріального вибору. Другий спосіб розв’язку таких задач полягає у виділенні основного, головного критерію та розгляд решти як додаткових, супутніх. Така відмінність критеріїв дозволяє сформулювати задачу вибору як задачу знаходження умовного екстремуму основного критерію:

x^* = arg (7)

при умові, що додаткові критерії залишаються на заданих їм рівнях. На Рис.19 б) наведений розв’язок задачі

x₁^* = arg .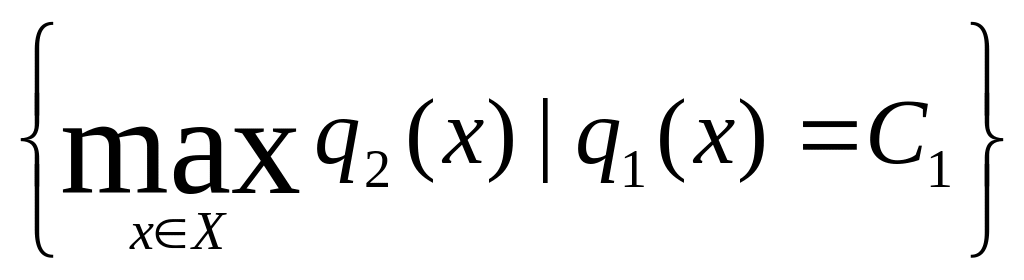

Удеяких задачах виявляється можливим або навіть необхідним задавати обмеження на супутні критерії не так жорстко, як узадачі (7). Наприклад, якщо супутній критерій характеризує вартість витрат, то замість фіксації витрат розумніше задавати їх верхній рівень, тобто формулювати задачу із обмеженнями типу нерівностей:

x^* = arg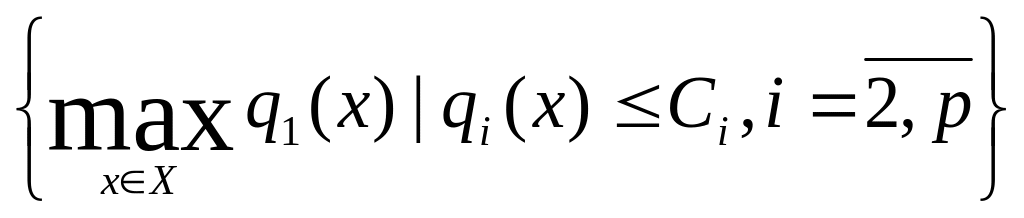 . (8)

На Рис.19 б наведений розв’язок задачі x₂^* = arg .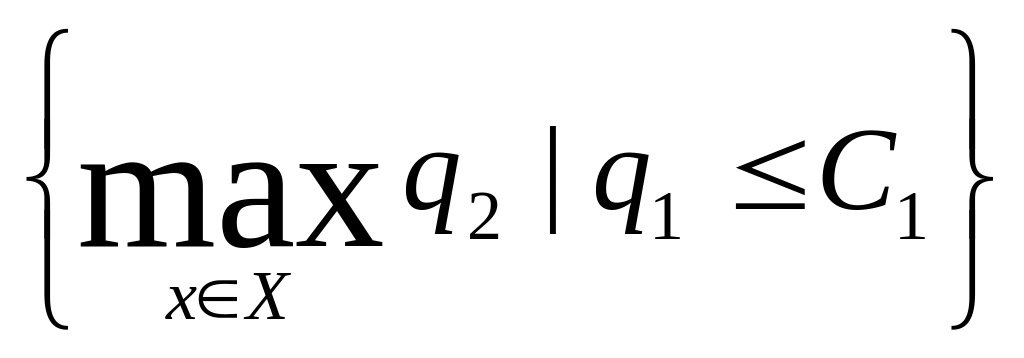

Розглянемо відмінності у постановках задач вибору.

Метод поступок. Нехай часткові критерії впорядковані у порядку зменшення їх важливості. Візьмемо перший із них та знайдемо найкращу по цьому критерію альтернативу (Рис.19 б). Це x₂^*, якщо найважливішим критерієм є q₂, та x₄^*, якщо їм являється q₁. Потім визначимо „поступку” q_i, тобто величину, на яку згодні зменшити досягнуте значення самого важливого критерію, щоби за рахунок поступки спробувати збільшити, наскільки це можливо, значення наступного по важливості критерію й т. д. На Рис. 19 б отримані таким чином альтернативи зображені точками x₃^* та x₅^*.