2.8 Задания к лабораторной работе № 2

Составить программы вычисления значений функций Y и Z, предусмотрев в них форматный вывод данных и результатов расчетов. Просчитать несколько раз с такими исходными данными, при которых выполнялись бы все условия в задании варианта.

Вариант № 1

1.1. используя условный арифметический оператор

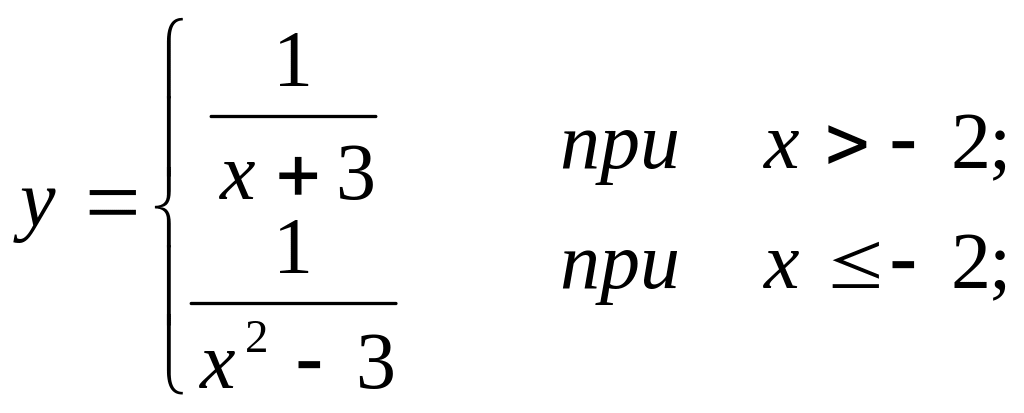
1.2. используя условный логический оператор

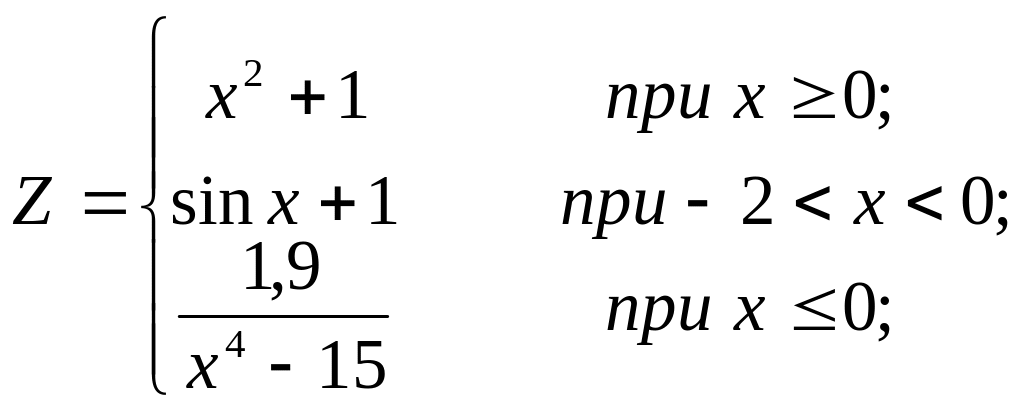
Вариант № 2

1. используя условный арифметический оператор

1.2. используя условный логический оператор

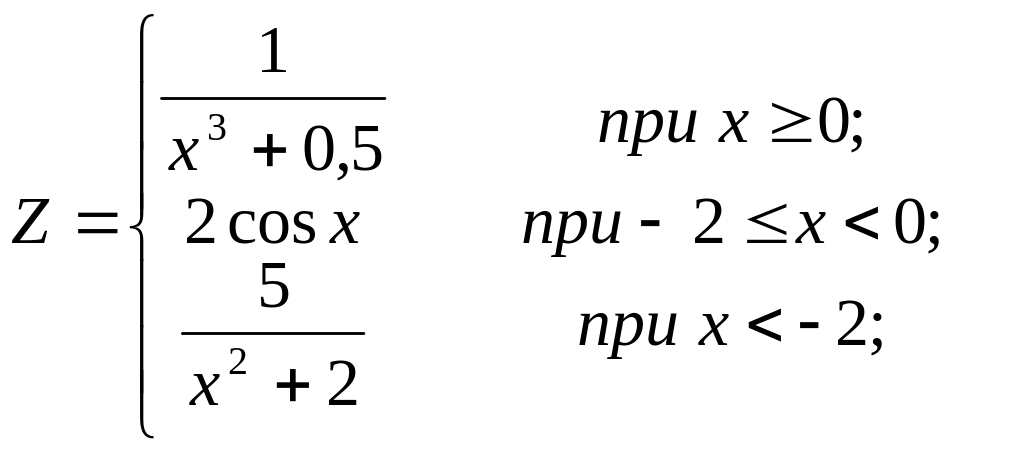
Вариант № 3

1. используя условный арифметический оператор

1.2. используя условный логический оператор

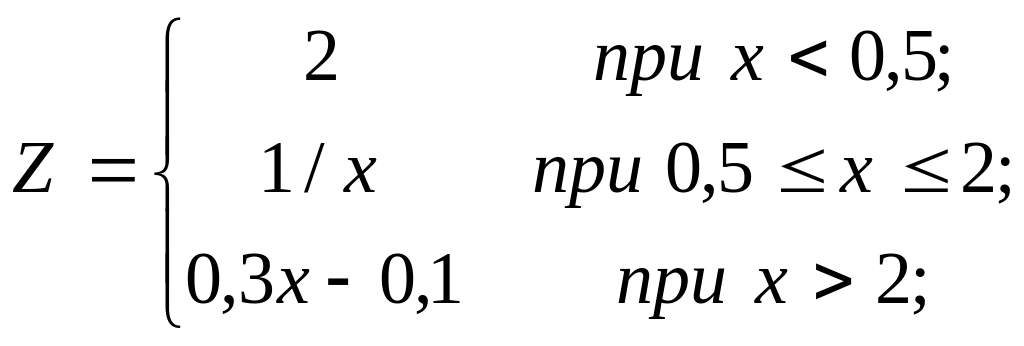
Вариант № 4

1. используя условный арифметический оператор

1.2. используя условный логический оператор

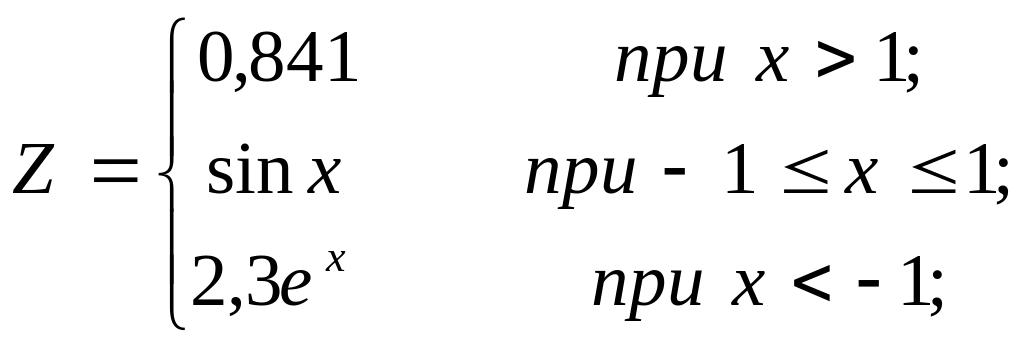
Вариант № 5

2. используя условный арифметический оператор

1.2. используя условный логический оператор

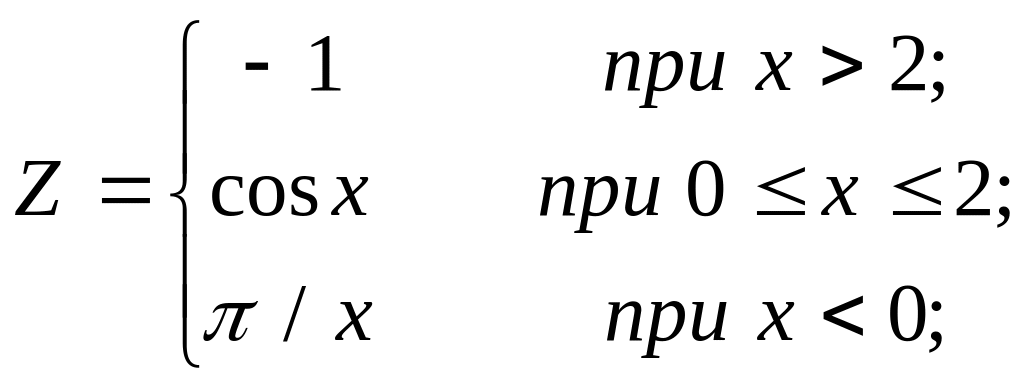
Вариант № 6

2. используя условный арифметический оператор

1.2. используя условный логический оператор

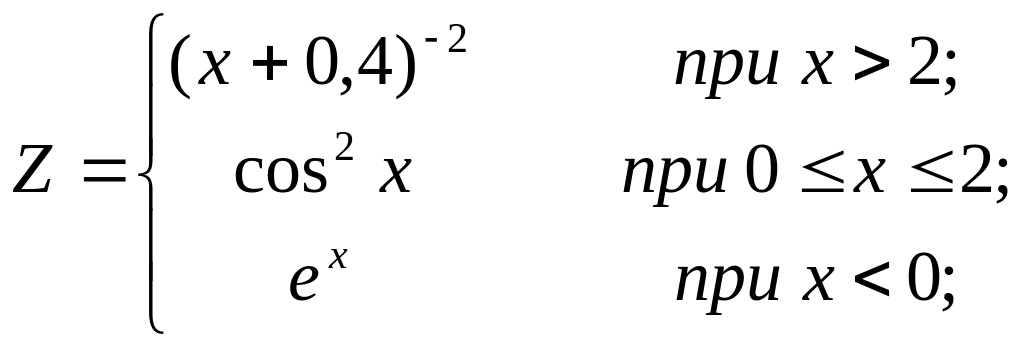
Вариант № 7

3. используя условный арифметический оператор

1.2. используя условный логический оператор

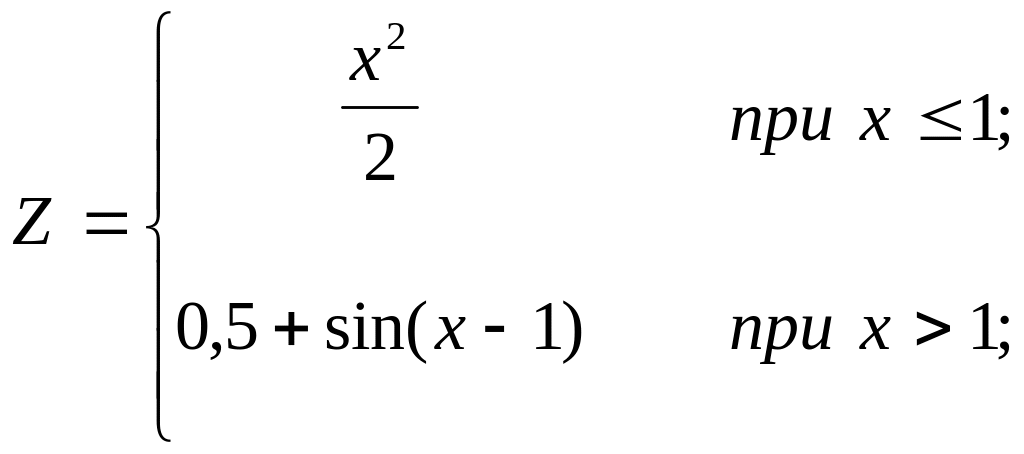
Вариант № 8

3. используя условный арифметический оператор

1.2. используя условный логический оператор

Раздел III. Лабораторная работа № 3

3.1 Циклический алгоритм

Рассмотрим пример циклического алгоритма, когда некоторые его пункты выполняются многократно. Например, требуется найти сумму n чисел. Пусть n = 3. Тогда программу можно представить в следующем виде:

*продолжение SUM 1

READ *, X

S = S + X

PRINT *, ' ВВЕД. ЗНАЧ. X '

READ *, X

S = S + X

PRINT *, ‘СУММА S =’ , S

END

PROGRAM SUM1

S = 0

PRINT*, 'ВВЕД. ЗНАЧ. X '

READ *, X

S = S + X

PRINT *, 'ВВЕД. ЗНАЧ. X’

В этой программе операторы ввода и присваивания повторяются три раза. Но если бы нужно было сложить 100 чисел, то эти операторы следовало бы повторить 100 раз. Естественно, возникает желание избежать стократного повторения операторов. Это можно сделать, составив программу таким образом, чтобы нужная группа операторов использовалась неоднократно. Это можно сделать, например, так:

*продолжение SUM2

S = S + A

K = K + 1

IF (K . LT. N) GO TO 1

PRINT 5, N, S

5 FORMAT (10X, ‘СУММА ‘,I 3,

*‘ЧИСЕЛ S =’, F10.4

END

PROGRAM SUM2

S = 0

K = 0

PRINT *,’ВВЕДИТЕ ЧИСЛО СЛАГАЕМЫХ N’

READ (5,*) N

1 PRINT *, ’ВВЕДИТЕ СЛАГАЕМОЕ A’

READ (5, *) A

Пример 2:

Пусть надо вычислить сумму некоторого ряда: S = x₁ + x₂ + …+ x _n. Если зафиксировать число n, то все этапы вычисления можно записать в виде линейного алгоритма. Например, для n=6 алгоритм вычисления суммы ряда можно представить так:

1. S положить равным 0.

2. S сложить с x₁; сумму S + x₁, считать новым значением S.

3. S сложить с x₂; сумму S + x₂ считать новым значением S,

и т.д. до сложения S с x₆.

Эту запись можно усовершенствовать – вместо слов «считать новым значением» или «положить равным» можно писать символ = . Тогда рассмотренный алгоритм будет выглядеть следующим образом:

5. S = S +x₄

6. S = S +x₅

7. S = S +x₆

8. Стоп

1. S = 0

2. S = S +x₁

3. S = S +x₂

4. S= S +x₃

Здесь все действия выполняются последовательно одно за другим и не

более чем по одному разу, т.е. алгоритм, является линейным. В п. 1 переменной S присваивается значение, равное нулю, и к моменту выполнения п.2 S=0. Поэтому в п. 2, где текущее значение S складывается с x₁, результат становится новым значением S. В п. 3 это новое значение S складывается с x₂, в результате чего S становится равным сумме x₁ и x₂. В п. 4 S становится равным сумме трех слагаемых x₁, x₂ и x₃ и т.д.

Легко заметить, что в пп. 2 –7 выполняются одинаковые действия. В каждом

пункте переменной S присваивается значение, равное суме текущего значения S и значения очередного слагаемого x₂, которое определяется значением индекса i, изменяющегося в нашем примере от 1 до 6. Учитывая сказанное, алгоритм вычисления суммы ряда можно записать короче:

1. S: = 0. 4. S: = S + x .

2. i: = 0. 5. Если i < 6, то перейти к п.3.

3. i: = i + 1. 6. Стоп.

В пунктах 1 и 2 присваивается начальное значение искомой сумме S и индексу i. Эти пункты и п. 6 выполняются по одному разу. А п.п. 3, 4 и 5 выполняются многократно, в данном случае шесть раз. Эти многократно выполняемые пункты образуют так называемый цикл. Особо важно то обстоятельство, что количество пунктов в цикле совершенно не зависит от количества повторений этих действий. Если бы нам надо было вычислить , то запись алгоритма осталась бы неизменным, за исключением п.5, в котором значение і сравнилось бы не с числом 6, а с числом 1000. В этом случае п.п. 3-5 выполнялись бы уже 1000 раз.

На этих примерах был продемонстрирован способ записи алгоритма,

который можно было бы назвать словесно-формульным.

Представим теперь в виде блок – схемы рассмотренный алгоритм вычисления суммы ряда (рис.6):

2) S:= 0; i := 0.

3) i := i + 1

4) S: = S + x .

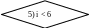
да нет

Рис. 6