Раздел II. Лабораторная работа № 2

2.1. Алгоритмы

Совокупности правил, позволяющие решить какую-либо задачу, называют алгоритмами. Таким образом, все мы живем в мире алгоритмов. Они экономят силы и время человека, так как однажды усвоенным алгоритмом он может пользоваться всю жизнь.

Разработка алгоритмов для решения задач на компьютере требует специальных навыков. Чтобы облегчить построение и проверку алгоритма, запись его должна быть понятной, наглядной, допускать возможность некоторых изменений алгоритма.

Алгоритмам присущ ряд свойств, которые и объясняют, почему исполнитель может получить решение какой–либо задачи без особого труда.

1. Дискретность. Алгоритм состоит из последовательности законченных действий - шагов. Переход к следующему шагу возможен лишь после завершения предыдущего. Это свойство алгоритма всегда состоять из отдельных завершенных шагов называется дискретностью.

2. Определенность. Чтобы исполнитель мог решать задачу по заданному алгоритму, необходимо, чтобы каждая команда алгоритма всегда однозначно понималась и точно исполнялась. Это значит, что любая команда, выполненная много раз или различными исполнителями при одних и тех же исходных данных всегда должна давать один и то же результат. Эти требования и составляют свойство определенности алгоритма. Чтобы исключить возможность неоднозначного понимания команд алго-ритма, для описания алгоритмов разработаны специальные языки, в которых каждое предложение имеет абсолютно точный смысл.

3. Массовость.С помощью алгоритма можно решать не одну конкурентную задачу, а множество однотипных задач. Эти требования можно выполнять, если, разрабатывая алгоритм, придерживаться так называемого структурного подхода – применять вспомогательные алгоритмы, описывать алгоритм с помощью трех основных структур: следования, ветвления, повторения. Эти структуры на рисунке. 2:

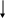
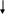
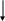
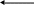
следования

ветвления

повторения

Рис. 2

2.2 Рассмотрим пример составления схем алгоритмов.

Составить схему поиска наибольшего значения из трех величин X1,X2,X3.

Положим U равным X1. Сравним теперь U с X2. Если U > X2, то остается его прежнее значение. Если же окажется, что U < X2, то принимается U = X2. Затем сравним U с X3_. Если U< X3, то U следует положить равным X3_. Таким образом, величине U будет присвоено значение наибольшего из трех заданных чисел.

Теперь алгоритм решения задачи можно представить более четко:

1. U положить равным X1

2. Если U ≥ X2, перейти к п. 4

3. U положить равным X2

4. Если U ≥ X3, перейти к п. 6

5. U положить равным X3

6. Стоп.

Несколько усовершенствуем форму записи алгоритма – вместо слов «положить равным» будем писать оператор присваивания = . Тогда предложенный алгоритм будет выглядеть следующим образом и иметь разветвляющуюся структуру (рис 3):