2. Структурные схемы электронных вольтметров постоянного и переменного тока.

Электронные вольтметры постоянного тока состоят из делителя входного напряжения, усилителя постоянного тока, и измерительного устройства, в качестве которого обычно используется магнитоэлектрических микроамперметр. Диапазон измерения составляет 100 мВ … 1000 В.

   

Электронный вольтметр переменного тока

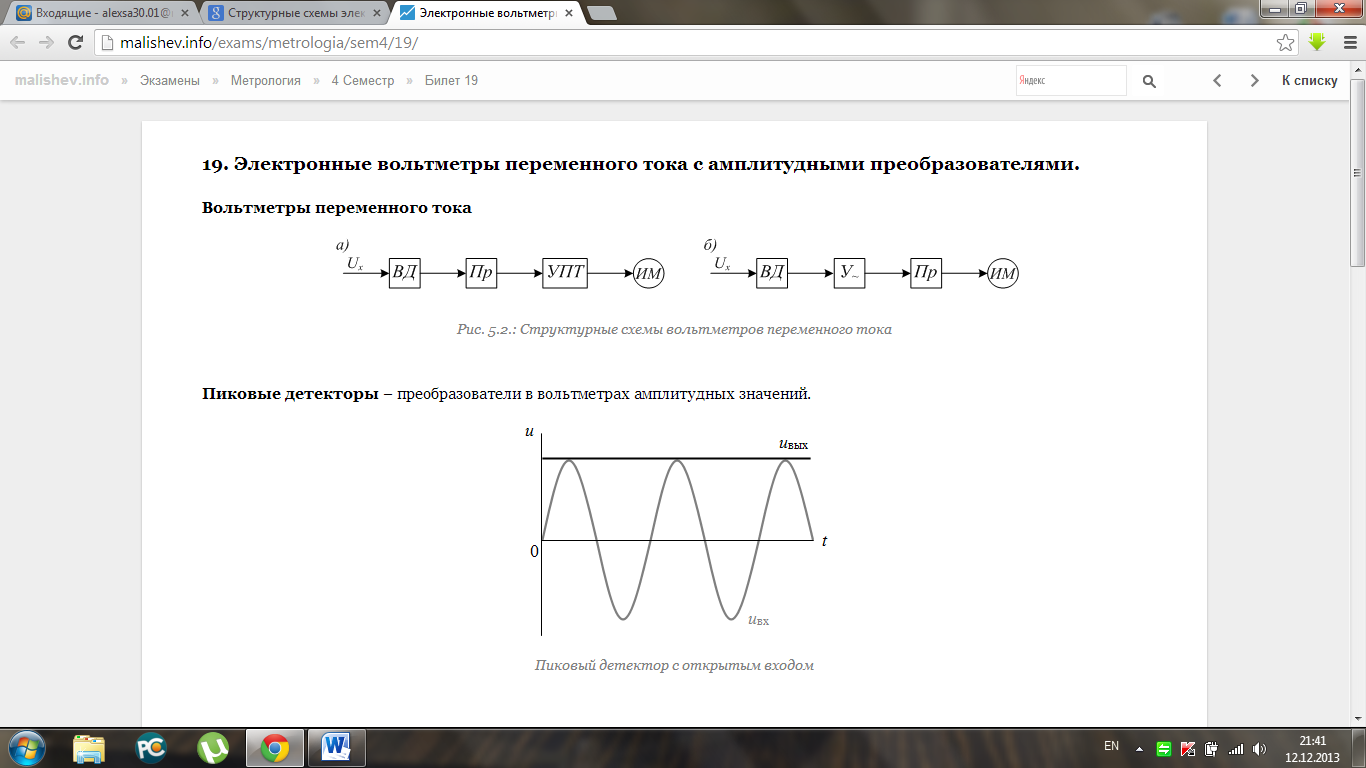
Электронные вольтметры переменного тока представляют собой сочетание выпрямителя на электровакуумных или полупроводниковых диодах, усилителя и магнитоэлектрического измерительного механизма. Электронные вольтметры переменного тока позволяют измерять максимальное ( пиковое) или действующее значение подводимого высокочастотного напряжения.

БИЛЕТ №15

1. Структурные схемы электронных вольтметров постоянного и переменного тока.

Электронные вольтметры постоянного тока состоят из делителя входного напряжения, усилителя постоянного тока, и измерительного устройства, в качестве которого обычно используется магнитоэлектрических микроамперметр. Диапазон измерения составляет 100 мВ … 1000 В.

   

Электронный вольтметр переменного тока

Электронные вольтметры переменного тока представляют собой сочетание выпрямителя на электровакуумных или полупроводниковых диодах, усилителя и магнитоэлектрического измерительного механизма. Электронные вольтметры переменного тока позволяют измерять максимальное ( пиковое) или действующее значение подводимого высокочастотного напряжения.

2. Основные характеристики цифровых приборов. Узлы цифровых приборов.

 Цифровыми измерительными приборами (ЦИП) называются приборы, которые в процессе измерения осуществляют автоматичес­кое преобразование непрерывной измеряемой величины вдискретную с последующей индикацией результата измерений на цифровом отсчетном устройстве или регистрацией его при помощи цифропечатающего устройства.

  Характеристики цифровых приборов:

1)     Статическая функция преобразования идеально-цифрового прибора.

Идеальный цифровой прибор – это прибор, у которого нет инструментальной погрешности, и он осуществляет отождествление с ближайшим уровнем квантования.

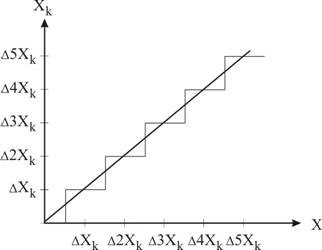
2) Погрешность измерительных приборов:

 - погрешность дискретности, имеет методическое основание.

 - погрешность, реализации уровней квантования.

 – погрешность из-за наличия порога чувствительности у устройства сравнения

 – погрешность из-за воздействия помех

 3) Погрешность дискретности:

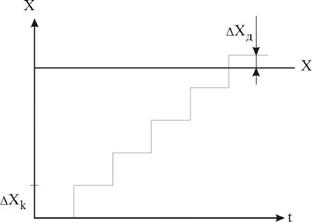
=     ( -случайная величина, с равномерным распределением)

 Больше/равно:            (систематическая погрешность)

Меньше/равно:           (систематическая погрешность)

Ближе/равно:            (систематическая погрешность)

Цифровые измерительные приборы обязательно включают два узла: аналого-цифровой преобразователь и цифровое отсчетное устройство.

БИЛЕТ № 16

1. Числовые параметры законов распределения.

Координаты центра распределения показывают положение случайной величины на числовой оси и могут быть найдены несколькими способами.

1. Центр симметрии – это такая точка x_m на оси x, слева и справа от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5.

т. М – медиана, 50%-ый квантиль.

2. Центр распределения можно найти как центр тяжести распределения. Это такая точка x, относительно которой опрокидывающий момент геометрической фигуры, огибающей которой является кривая M(x). Точка эта называется мат. ожиданием.

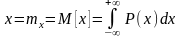
3. Для двух модальных распределений применяется оценка центра в виде центра сгибов.

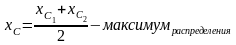
4. Для ограниченных распределений (равномерноетрапециидальное) оценка центров рассматривается в виде центров размаха.

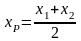
x₁ – крайний левый, x₂ – крайний правый.

Моменты распределений.

Начальный и центральный моменты k-го порядка определяются соответственно по формулам

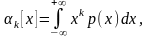
где  – центральный момент, k – порядок момента.

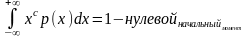
Он используется для задания условия нормирования плотности распределения.

1) k=1

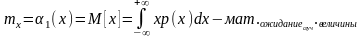
2) 2-ой центральный момент

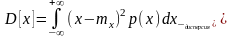
3) 3-ий центральный момент

Служит для характеристики асимметрии или искаженности распределения.

Коэффициент асимметрии

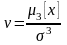
Для нормального коэф-та

асимметрии =0.

4) Центральный момент 4-го порядка

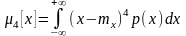
Служит он для харак-ки остро- или плосковершинности распределения. Описывается с помощью эксцесса:

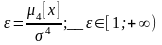
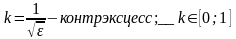
Энтропийное значение погрешности.

Энтропийный интервал определяется по след.формуле

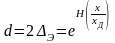, где_Э – энтропийное значение погр-ти.

H – энтропия действительного значения x измеряемой величины вокруг полученного после измерения значения x_Д, т.е. энтропия погр-ти измерений.

Достоинство: строгое определение доверител. интервала.

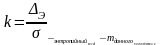
2. Суммирование систематических и случайных погрешностей.

Систематической погрешностью называется погрешность, остающаяся постоянной или закономерно изменяющейся во времени при повторных измерениях одной и той же величины.

Примером систематической погрешности, закономерно изменяющейся во времени, может служить смещение настройки прибора во времени.

Случайной погрешностью измерения называется погрешность, которая при многократном измерении одного и того же значения не остается постоянной. Например, при измерении валика одним и тем же прибором в одном и том же сечении получаются различные значения измеренной величины.

Систематические и случайные погрешности чаще всего появляются одновременно.

Для выявления систематической погрешности производят многократные измерения образцовой меры и по полученным результатам определяют среднее значение размера. Отклонение среднего значения от размера образцовой меры характеризует систематическую погрешность, которую называют «средней арифметической погрешностью», или «средним арифметическим отклонением».

Систематическая погрешность всегда имеет знак отклонения, то есть «+» или «-». Систематическая погрешность может быть исключена введением поправки.

При подготовке к точным измерениям необходимо убедиться в отсутствии постоянной систематической погрешности в данном ряду измерений. Для этого существуют специальные методы.

Прогрессивные и периодические систематические погрешности в противоположность постоянным можно обнаружить при многократных измерениях.

Обработка данных и оценка параметров случайных погрешностей производится методами математической статистики

При расчете предельной погрешности измерения определяют числовое значение погрешности измерения от всех составляющих и производят суммирование:

где знаки «+» или «-» ставятся из условия, чтобы систематические и случайные погрешности суммировались по модулю.

Если в случайной погрешности известно среднее квадратическое отклонение, то

где  К — показатель, указывающий доверительные границы для предельной случайной погрешности измерения (при К = 1 р = 0,65; при К = 2 р = 0,945; при К = 3 р = 0,9973).

Если результаты измерений зависят от большого числа разнообразных факторов, то

где   X_i — переменные функциональные параметры.

Каждый параметр может иметь отклонение Δx_i (погрешность) от предписанного значения x_i. Поскольку погрешность Δx_i мала по сравнению с величиной x_i суммарная погрешность Δx_y функции y можно вычислять по формуле:

где   dy/dx_i — передаточное отношение (коэффициент влияния) параметра x_i.

Формула (3.1) справедлива лишь для систематических погрешностей Δx_i.

Для случайных погрешностей (когда отдельные составляющие не всегда принимают предельные значения) используются теоремы теории вероятностей о дисперсии, то есть

Суммарная погрешность при наличии только случайных составляющих δx_i погрешностей

где

m — число попарно корреляционно связанных параметров;  ki и kj коэффициенты относительного рассеяния, характеризующие степень отличия закона распределения погрешности данного параметра от нормального;  rij — коэффициент корреляции, существующий при наличии корреляционной связи между параметрами xi и xj

При наличии и систематических и случайных составляющих погрешностей вычисляют доверительные границы суммарной погрешности:

где  k — масштабный коэффициент интервала распределения, зависящий от закона распределения и принятой доверительной вероятности.

Так, при доверительной вероятности Р = 0,95 для закона нормального распределения k= 2, а для закона Максвелла k = 3,6.

БИЛЕТ №17

1. Математические модели сложных измерительных сигналов.

В средствах измерений используется большое число измерительных сигналов, имеющих самые разнообразные формы. Рассмотрим некоторые из них, наиболее часто встречающиеся на практике. Прямоугольные импульсы. Одиночный идеальный прямоугольный импульс (рис. 10.7,а) описывается уравнением т.е. он формируется как разность двух единичных функций, сдвинутых во времени на величину т — длительность импульса. 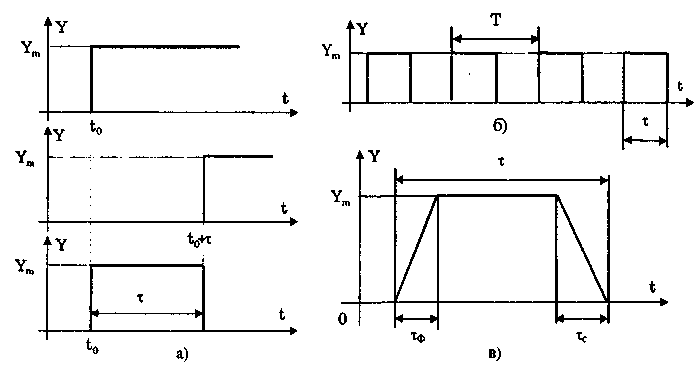Рис. 10.7. Формирование идеального прямоугольного импульса (а),  последовательность прямоугольных импульсов (б) и трапецеидальный импульс (в) Последовательность прямоугольных импульсов есть сумма одиночных импульсов: Для ее описания необходимо знать три параметра: амплитуду Y_m, длительность Т и период Т (рис. 10.7, б). Отношение периода к длительности прямоугольного импульса называется скважностью, а обратная величина — коэффициентом заполнения. При скважности, равной двум, последовательность импульсов называют меандром (см. рис. 10.7, б). Идеальные прямоугольные импульсы в природе не встречаются. В реальных импульсах время изменения сигнала от нулевых до амплитудных значений (и обратно) всегда имеет конечную длительность, т.е. фронт Т_ф и спад Т_с (рис. 10.7, в). Следовательно, у реальных импульсов будет трапецеидальная форма. Трапецеидальный импульс также является идеализации реальных импульсов, которые имеют гораздо более сложную форму. Она отличается от трапеции спадом вершины импульса, выбросами на вершине и в паузе и другими особенностями, учтенными в системе параметров реального прямоугольного импульса по ГОСТ 16465-70. Сигналы с линейными участками. При построении средств измерительной техники широкое применение находят периодические сигналы с линейными участками. Это прежде всего линейный знакопеременный и однополярный линейно изменяющийся (пилообразный) сигналы (рис. 10.8). 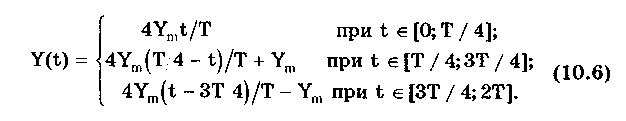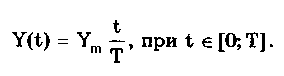Линейный знакопеременный сигнал описывается уравнением Пилообразный сигнал 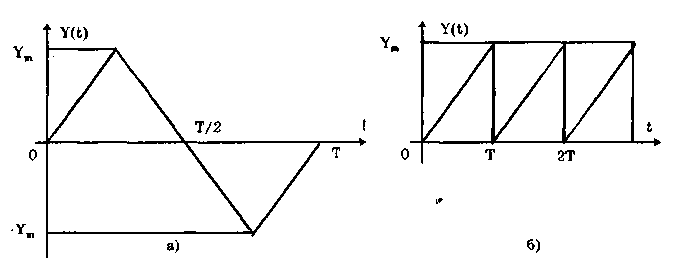Рис. 10.8. Линейный знакопеременный (а) и однополярный линейно изменяющийся (пилообразный) (б) сигналы Модулированные сигналы. Модулированным называется сигнал, являющийся результатом взаимодействия двух или более сигналов, т.е. модуляции. Модуляция — это воздействие измерительного сигнала X(t) на какой-либо параметр стационарного сигнала Y(t), обладающего такими физической природой и характером изменения во времени, при которых удобны его дальнейшие преобразования и передача. В качестве стационарного сигнала, именуемого несущим, обычно выбирают синусоидальное (гармоническое) колебание  (10.7) или последовательность импульсов. Физический процесс, обратный модуляции, называется демодуляцией, или детектированием, и заключается в получении из модулированного сигнала другого сигнала, пропорционального модулирующему. Задача демодуляции — по возможности полное восстановление информации, содержащейся в модулирующем сигнале X(t). Вид модуляции и способ детектирования зависят от требований, предъявляемых к точности передачи информации. Наиболее простым модулированным гармоническим сигналом является амплитудно-модулированный сигнал, в котором измерительная информация содержится в амплитуде несущего синусоидального сигнала (рис. 10.9). 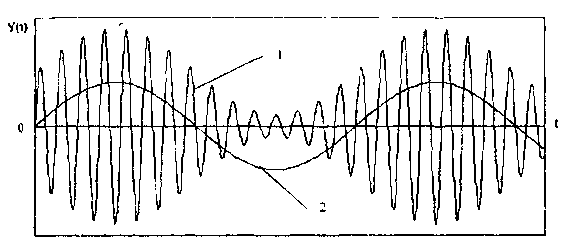Рис. 10.9. Амплитудно-модулированный (1) и модулирующий (2) сигналы  Амплитудно-модулированные сигналы описываются формулой  (10.8) где m — глубина амплитудной модуляции (всегда меньше единицы). При частотной модуляции (рис. 10.10) измерительная информация содержится в частоте модулированного сигнала, т.е. где _ — наибольшее изменение частоты модулированного сигнала, т.е. девиация частоты, пропорциональная амплитуде модулирующего сигнала. При фазовой модуляции (рис. 10.11) модулирующий сигнал X(t) воздействует на фазу несущего колебания: где m_ф — коэффициент фазовой модуляции. 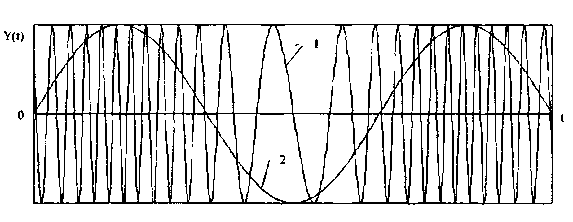Рис. 10.10. Частотно-модулированный (1) и модулирующий (2) сигналы Для того чтобы при детектировании можно было восстановить модулирующий сигнал, необходимо иметь сигнал вида (10.7), называемыйопорным. Относительно него наблюдают, как меняется фаза модулированного сигнала. Модулирующий, модулированный и опорный сигналы показаны на рис. 10.11. 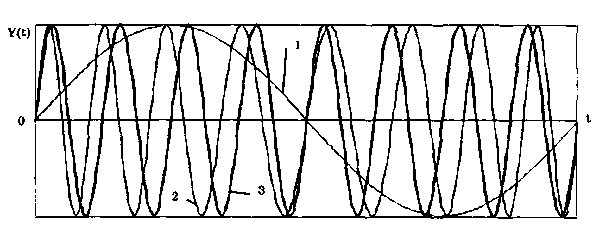Рис. 10.11. Модулирующий (1), фазомодулированный (2) и опорный (3) сигналы Если модулируемым сигналом является периодическая последовательность прямоугольных импульсов, уо возможны три вида модуляции (рис. 10.12): • амплитудно-импульсная (АИМ); • частотно-импульсная (ЧИМ); • широтно-импульсная (ШИМ). 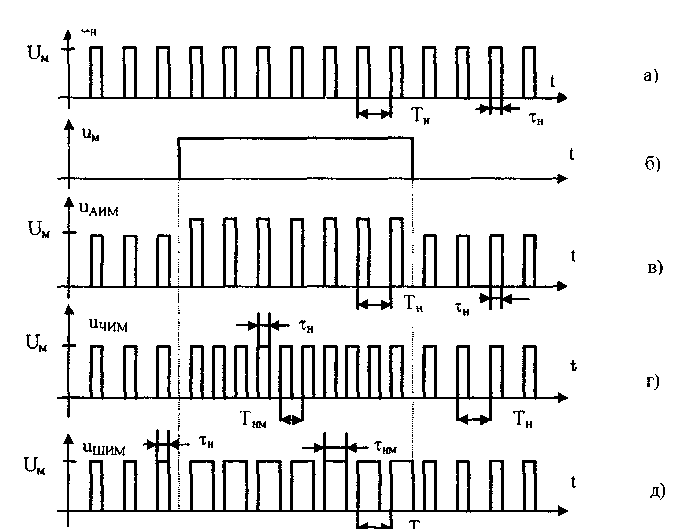Рис. 10.12. Несущая последовательность прямоугольных импульсов (а), модулирующий (б), амплитудно-модулированный (в), частотно-модулированный (г) и широтно-модулированный (д) сигналы При этом параметром, несущим измерительную информацию, соответственно являются амплитуда, частота и длительность импульсов.