
- •Екзаменаційний білет № 1
- •Квантова гіпотеза та формула Планка
- •Радіоактивність
- •Екзаменаційний білет № 2
- •Ефект Комптона
- •Ядерні реакції. Реакція поділу
- •Екзаменаційний білет № 3
- •Теплове випромінювання, його основні визначення
- •Склад ядра атома. Ізотопи
- •Екзаменаційний білет № 4
- •Оптична пірометрія.
- •Закон радіоактивного розпаду
- •Екзаменаційний білет № 5
- •Закон Стефана-Больцмана
- •Енергія зв’язку ядра
- •Екзаменаційний білет № 6
- •Закон Кірхгофа.
- •Дефект маси ядра
- •Екзаменаційний білет № 7
- •Закон Малюса
- •Електронно-дірковий перехід
- •Екзаменаційний білет № 8
- •Закон Віна.
- •Ядерні сили
- •Екзаменаційний білет № 9
- •Розсіювання та поглинання світла.
- •Зонні моделі металів, діелектриків та напівпровідників
- •Екзаменаційний білет № 10
- •Поляризація світла
- •Теплові властивості твердих тіл. Закон Дюлонга і Пті, квантові теорії теплоємності
- •Екзаменаційний білет № 11
- •Закон Брюстера
- •Власна та домішкова проводимість напівпровідників
- •Екзаменаційний білет № 12
- •Електромагнітні хвилі, швидкість їх розповсюдження.
- •Екзаменаційний білет № 13
- •Інтерференція світла.
- •Експериментальні дослідження кришталів
- •Екзаменаційний білет № 14
- •Дифракція світла.
- •Кристалічна решітка, дефекти в кришталах
- •Екзаменаційний білет № 15
- •Дисперсія світла.
- •Енергетичні зони в кристалах
- •Екзаменаційний білет № 16
- •Затухаючі коливання.
- •Квантові числа, принцип Паулі
- •Екзаменаційний білет № 17
- •Коливальний контур, формула Томсона
- •Спектральні серії
- •Екзаменаційний білет № 18
- •Математичний та фізичний маятники
- •Рівняння Шредінгера
- •Екзаменаційний білет № 19
- •Хвильова функція та її статистичний зміст
- •Гармонічні коливання
- •Екзаменаційний білет № 20
- •Вимушені коливання
- •Досліди Резерфорда по розсіюванню α-частинок речовиною
- •Екзаменаційний білет № 21
- •Резонанс
- •Іонні та ковалентні молекули
- •Екзаменаційний білет № 22
- •Зовнішній фотоефект
- •Правила зміщення
- •Екзаменаційний білет № 23
- •Екзаменаційний білет № 24
- •Рівняння Ейнштейна для зовнішнього фотоефекту
- •Співвідношення невизначеностей
Рівняння Шредінгера
Статистическое толкование
волн де Бройля и соотношение
неопределенностей Гейзенберга привели
к выводу, что уравнением движения в
квантовой механике, описывающим движение
микрочастиц в различных силовых
полях, должно быть уравнение, из
которого бы вытекали наблюдаемые на
опыте волновые свойства частиц.
Основное уравнение должно быть уравнением
относительно волновой функции ![]() ,
так как именно она, или, точнее, величина
,
так как именно она, или, точнее, величина ![]() ,
определяет вероятность пребывания
частицы в момент времени t в объеме
,
определяет вероятность пребывания
частицы в момент времени t в объеме![]() ,
т. е. в области с координатами х и x+dx, у
и у+dy, z и z + dz. Так как искомое уравнение
должно учитывать волновые свойства
частиц, то оно должно быть волновым
уравнением, подобно уравнению,
описывающему электромагнитные волны.
,
т. е. в области с координатами х и x+dx, у
и у+dy, z и z + dz. Так как искомое уравнение
должно учитывать волновые свойства
частиц, то оно должно быть волновым
уравнением, подобно уравнению,
описывающему электромагнитные волны.
Основное уравнение нерелятивистской квантовой механики сформулировано Э. Шредингером. Уравнение Шредингера, как и все основные уравнения физики (например, уравнение Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид
![]() (18.2.1)
(18.2.1)
где ![]() ,
m – масса частицы,
,
m – масса частицы, ![]() –
оператор Лапласа
–
оператор Лапласа 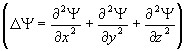 ,
i – мнимая единица,
,
i – мнимая единица, ![]() -
потенциальная энергия частицы в силовом
поле, в котором частица движется.
-
потенциальная энергия частицы в силовом
поле, в котором частица движется.
Задача. Визначити максимальну енергію фотона при спостереженні серії Бальмера.

Екзаменаційний білет № 19
Хвильова функція та її статистичний зміст
М. Борн предположил, что по волновому
закону меняется не сама вероятность,
а некая величина, названная амплитудой
вероятности, обозначаемая![]() .
Эту величину называют также волновой
функцией (или
.
Эту величину называют также волновой
функцией (или ![]() -функцией).
Амплитуда вероятности может быть
комплексной, и вероятность W пропорциональна
квадрату ее модуля:
-функцией).
Амплитуда вероятности может быть
комплексной, и вероятность W пропорциональна
квадрату ее модуля:
![]() (19.1.1)
(19.1.1)
Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени t в области с координатами х и х + dx, у и у + dy. : и z + dz.
Итак, в квантовой механике состояние микрочастиц описывается принципиально по-новому — с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых свойствах. Вероятность нахождения частицы в элементе объема dV равна
![]() ,
(19.1.2)
,
(19.1.2)
где величина ![]()
(квадрат модуля Т-функции) имеет смысл
плотности вероятности. Таким образом,
физический смысл имеет не сама
-функция,
а квадрат ее модуля ![]() (
(![]() -функция,
комплексно-сопряженная с
),
которым определяется интенсивность
волн де Бройля.
-функция,
комплексно-сопряженная с
),
которым определяется интенсивность
волн де Бройля.
Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме сложения вероятностей, равна
![]() .
.
Поскольку ![]() определяется
как вероятность, необходимо волновую
функцию Т нормировать так, чтобы
вероятность W достоверного события
обращалась в единицу, если за объем
V принять бесконечный объем всего
пространства. Это означает, что при
данном условии частица должна находиться
где-то в пространстве. Следовательно,
условие нормировки вероятностей
определяется
как вероятность, необходимо волновую
функцию Т нормировать так, чтобы
вероятность W достоверного события
обращалась в единицу, если за объем
V принять бесконечный объем всего
пространства. Это означает, что при
данном условии частица должна находиться
где-то в пространстве. Следовательно,
условие нормировки вероятностей
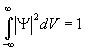 (19.1.3)
(19.1.3)
где тройной интеграл (19.1.3) вычисляется
по всему бесконечному пространству, т.
е. по координатам х, у. z от ![]() до
до ![]() .
Таким образом, условие (19.1.3) говорит об
объективном существовании частицы во
времени и пространстве.
.
Таким образом, условие (19.1.3) говорит об
объективном существовании частицы во
времени и пространстве.
Чтобы волновая функция являлась объективной характеристикой состояния микрочастиц, она должна удовлетворять ряду ограничительных условий. Функция Т, характеризуя вероятность обнаружения действия микрочастицы в элементе объема, должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть не однозначной величиной) и непрерывной (вероятность не может изменяться скачком).
Волновая функция удовлетворяет принципу
суперпозиции: если система может
находиться в различных состояниях,
описываемых волновыми функциями ![]() то она также может находиться в
состоянии
,
описываемом линейной комбинацией
этих функций:
то она также может находиться в
состоянии
,
описываемом линейной комбинацией
этих функций:
![]()
где Сn (n = 1,2,…) — некоторые комплексные числа. Сложение волновых функций (амплитуд вероятностей), а не вероятностей (квадратов волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей.
Зная волновую функцию в квантовой механике, вычисляют средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние <r> электрона от ядра вычисляют по формуле:
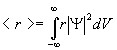
где интегрирование производится, как и в случае (19.1.3).
