Екзаменаційний білет № 16

1. Затухаючі коливання.

Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.

(16.1.1)

где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ 

или

(16.1.2)

Перепишем это уравнение в следующем виде:

и обозначим:

где   представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда

(16.1.3)

Будем искать решение уравнения (16.1.3) в виде где U - некоторая функция от t.

Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (6.1.3), получим 

Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение   тогда с вещественным ω решением этого уравнения, как мы знаем, является функция 

Таким образом, в случае малого сопротивления среды   , решением уравнения (16.1.3) будет функция

(16.1.4)

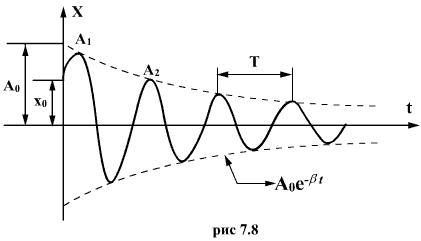
График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину   называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину   обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,

Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.

Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда

откуда

Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.

Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда

Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз

2. Квантові числа, принцип Паулі

Движение электрона в атоме описывается 5 квантовыми числами: главным n, побочным (орбитальным) l, магнитным ml, спиновым s и проекцией спина (магнитным спиновым числом) ms.

Главное квантовое число n определяет общую энергию электрона. Оно может принимать любые целые значения начиная с единицы (n=1,2,3,…).

Побочное (орбитальное ) квантовое число l характеризует форму орбитали. Оно может принимать целые значения от 0 до n-1 (l=0,1,…,n-1).

l принято обозначать буквенными символами:

Значение l 0 1 2 3 4

Буквенное обозначение s p d f g

Обычно рассматривают s-, p-, d-, f-, g-орбитали.

n l Обозначение орбитали

1 0 1s

2 0,1 2s,2p

3 0,1,2 3s,3p,3d

4 0,1,2,3 4s,4p,4d,4f

n, l – квантовые числа.

Орбитали с одинаковыми значениями n называются оболочкой (Энергетическим уровнем), с одинаковыми значениями n и l – подоболочкой (подуровнем).

Магнитное квантовое число ml характеризует направление орбитали в пространстве (проекцию на выбранное направление, например, на ось z). Оно может принимать любые целые значения от –l до +l, включая 0. Например, при l=0 ml=0; при l=1 ml=-1,0,+1. При заданном n возможна одна s-орбиталь, три p-орбитали, пять d-орбиталей и семь f-орбиталей.

Каждый электрон характеризуется спиновым квантовым числом s. Спин – собственный момент импульса электрона, не связанный с движением в пространстве. Абсолютное значение спина s=1/2. Проекция спина на ось z (магнитное спиновое число) ms=+1/2 или ms=-1/2.

Принцип Паули. В атоме не может быть двух электронов, у которых все четыре квантовых числа были бы одинаковы. Или, на каждой орбитали может может находиться не более двух электронов.

Задача. Чому дорівнює максимальна швидкість електронів, що вилітають з Ag при освітленні його променями з довжиною хвилі 280 нм.