6.2 Определение геометрических параметров зубчатых колес.

Все размеры зубчатого колеса пропорциональны модулю и определяются по формулам:

высота головки зуба h_a= m; принимаем m=1

высота ножки зуба h_f = 1.25 m;

высота зуба h = 2.25 m;

диаметр делительной окружности = m z;

диаметр окружности вершин зубьев d_a= ;

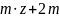диаметр окружности впадин зубьев d_f = ;

угловой шаг зацепления = 2 /z;

окружной шаг зацепления p=  m;

толщина зуба по делительной окружности s= 1/2  m;

межосевое расстояние a= ½ m (z₁ z₂).

Все расчеты зубчатых колес и формулы для расчета сводим в таблицу 6.2

Таблица 6.2. Определение геометрических параметров зубчатых колес.

Параметры	Формула
Число зубьев		30	30	32	28
высота головки зуба	ha= m	1	1	1	1
высота ножки зуба	hf = 1,25 m	1,25	1,25	1,25	1,25
высота зуба
диаметр делительной окружности		30	30	32	28
толщина зуба по делительной окружности	s= 1/2	1,57	1,57	1,57	1,57
диаметр окружности вершин зубьев	da=	32	32	34	30
диаметр окружности впадин зубьев	df =	27,5	27,5	29,5	25,5
угловой шаг зацепления	= 2 /z	0,21	0,21	0,196	0,224
окружной шаг зацепления		3,14	3,14	3,14	3,14
межосевое расстояние		45		45

6.3 Определение коэффициента полезного действия зубчатого механизма

.

Коэффициент полезного действия рассчитывается в зависимости от передаточного отношения и типа входного звена планетарного механизма. Так входным звеном является зубчатое колесо, а не водило, КПД рассчитывается по формуле:

где 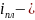передаточное отношение планетарной ступени;

КПД обращенного механизма.

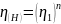
где 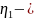коэффициент полезного действия каждой пары колес ( )

число пар колес планетарной ступени редуктора (n=2)

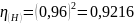
Найдем общий КПД зубчатого механизма:

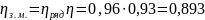
Вывод: Число зубьев в редукторе на зубчатых колесах не менее 18 и не более 200, поэтому редуктор получается габаритным. В редукторе установлено три блока сателлитов, КПД редуктора достаточно высок и делает редуктор пригодным к эксплуатации с малыми потерями.

27