2.7. Визначення загальних втрат напору при русі рідини

в простому трубопроводі

Задача № 2.71. Визначити втрати напору при подачі води із швидкістю

v = 13,1 см/сек, при температурі t = 10 °С по трубопроводу діаметром

d = 200 мм, довжиною l = 1500 м. Труби – нові, стальні.

Рішення: Визначимо режим руху рідини, прийнявши для t = 10˚С кінематичний коефіцієнт в’язкості υ = 0,0131 см²/сек (додаток I)

.

Так як Re = 20000 > 2320, то режим руху турбулентний. Знайдемо число Рейнольда, що відповідає межі гладкої зони:

.

Для нових стальних труб висота шорсткості Δ ≈ 0,45 мм. Приймемо

Δ = 0,45 мм, знайдемо:

.

Так як число Re = 20000 < 2 8667, то даний випадок відповідає області гладких труб.

Знайдемо λ за формулою Конакова:

.

Визначаємо втрати напору

м ≈ 0,17м.

Задача № 2.72. По трубопроводу діаметром d = 100 мм, шорсткість внутрішніх стінок якого ∆ = 0,2 мм, пропускається вода з витратою Q = 310^-2 м³/c на відстань L = 100 м. Сумарний коефіцієнт місцевих опорів _і = 12. Кінематичний коефіцієнт в’язкості  = 110^-6 м²/с. Визначити сумарні втрати напору Н_в (м).

Рішення: Сумарні втрати напору Н_в визначаються за формулою:

Н_в = h_l + h_м,

де h_l – втрати напору по довжині трубопроводу, h_м – втрати напору на подолання місцевих опорів.

Оскільки трубопровід простий (не має розгалужень, d = const), то сумарні втрати можна знайти як

.

Знаходимо значення швидкості руху рідини:

= 3,82 м/с.

Знаходимо режим руху рідини:

= = 381971

Отже, режим руху – турбулентний. Визначимо вид турбулентного руху:

= = 764 – 3 вид турбулентного руху.

Для визначення значення коефіцієнта тертя використаємо формулу Шифрінсона:

= 0,023

Підставивши знайдені значення швидкості, коефіцієнта тертя та параметрів, наданих в умові задачі, отримаємо:

= 26,32 м.

Знайдемо значення втрати напору в одиницях тиску

Па.

2.8. Витікання рідини через насадки і короткі трубопроводи

при постійному напорі

Задача № 2.78. До відкритого резервуару (рис. 2.32) з правої сторони приєднаний короткий стальний трубопровід, який складається з двох ділянок довжиною l₁ = 5 м і l₂ = 12 м діаметрами d₁ = 210^-2 м; і d₂ = 110^-2 м та оснащений краном, коефіцієнт опору якого ξ_кр = 3.

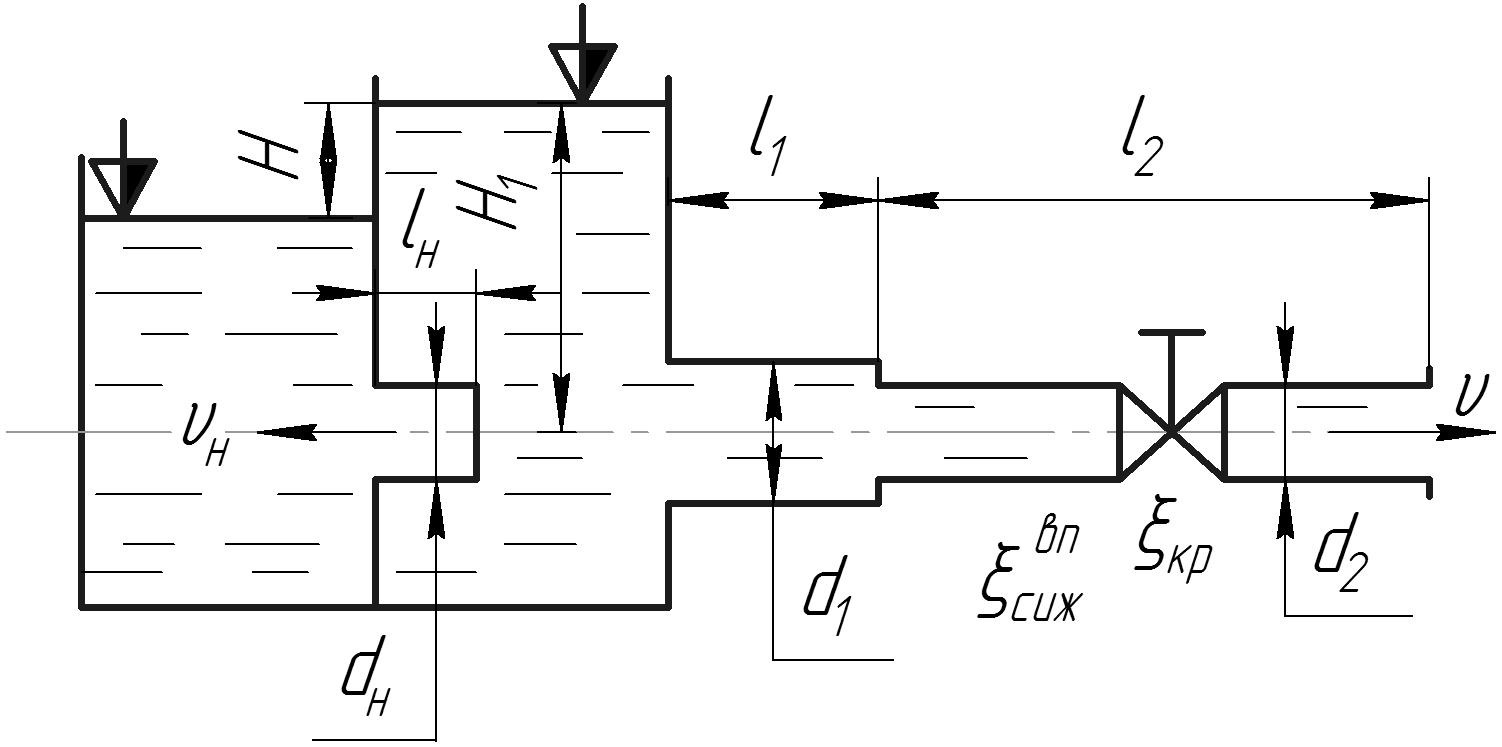
Рис. 2.32

Вода витікає у вільний простір по короткому трубопроводу під постійним напором Н₁ = 2,5 м. З лівої сторони приєднаний внутрішній циліндричний насадок (насадок Борда) діаметром d_н = 110^-2 м і довжиною l_н=5d_н з коефіцієнтом витрати μ_h = 0,71. Коефіцієнти гідравлічного тертя відповідно ₁ = 0,025; ₂ = 0,03. Витікання відбувається при різниці рівнів в резервуарах Н = 1 м.

Визначити: швидкість v і витрату Q води з короткого трубопроводу, витрату через насадок Q_H.

Рішення: При рішенні даних задач приймається, що діючий напір витрачається на подолання сумарних перешкод; тоді

. (1)

Оскільки значення швидкостей v₁ і v₂ невідомі, то використаємо для рішення умову нерозривності потоку рідини

Q₁ = Q₂ = v₁S₁ = v₂S₂; звідки . (2)

Підставивши даний вираз в (1), можна знайти швидкість на другій ділянці трубопроводу:

.

Знайдемо невідомі складові даного рівняння.

= 3,1410^-4 м²; = 7,8510^-4 м²; = 0; = 3.

Отже

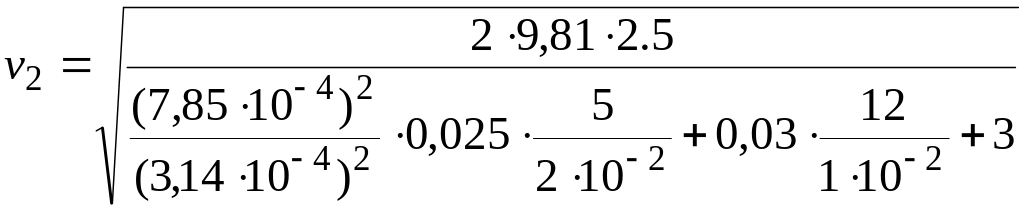
= 1,116 м/с.

Підставивши в (2), знайдемо швидкість рідини на першій ділянці

= 0,28 м/с.

Значення витрати знайдемо з виразу (2), наприклад, як

Q = Q₁ = v₁S₁ = 0,283,1410^-4 = 8,7610^-5 м³/с.

Витрату через насадок знайдемо як

; (3)

де - діючий напір над насадком. Для нашого випадку = H = 1 м. Площа поперечного перерізу насадка

= 7,8510^-5 м²/с. Підставляючи в (3), отримаємо:

= 310^-4 м³/с.