17. Бір электронды атомның кванттық сандары және бұлардың физикалық мағынасы.

Қазiргi атом теориясына сәйкес атомдағы электрон күйiн n, , j, m_j төрт кванттық сан жиынымен сипаттауға болады. n-бас кванттық сан; бiрiншi жуықтауда атомдағы электрон энергиясын анықтайды және n=1, 2, 3,... мәндерiн қабылдайды. -орбиталық кванттық сан, электронның орбиталық импульс моментiн анықтайды; =0, 1, 2,..., n-1 мәндерiн, барлығы n мән қабылдайды.

j-iшкi кванттық сан, атомдағы электронның толық импульс моментiн анықтайды;  және s берiлген жағдайда j=+s, +s-1,..., +s-1, барлығы 2s+1 мән қабылдайды.

m_j-магниттiк iшкi кванттық сан, электронның толық импульс моментiнiң оқшауланған бағытқа (магнит өрiсi бағытына) проекциясы шамасын анықтайды. Берiлген j жағдайында m_j=j, j-1, j-2,...-j, барлығы 2j+1 мән қабылдайды.

19.Спин-орбиталық әсерлесу. Сутегі атомы энергия деңгейлері мен спектрлік сызықтардың нәзік түзілісі.

Сутегi атомы энергетикалық деңгейлерiнiң нәзiк түзілiсi

Сутегi атомы энергетикалық деңгейлерiнiң нәзiк түзілiсiн екi физикалық фактор туғызады: 1) релятивтiк эффект-атомдағы электрон массасының оның ядроны айнала қозғалғандағы жылдамдығына тәуелдiлiгi; 2) электронның меншiктi магнит моментi мен электронның ядроны айнала қозғалысы туғызатын магнит өрiсiнiң әсерлесуi.

Электронның спинi және оның орбиталық қозғалысымен байланысты фактор да релятивтiк болып табылады.

Шредингер теңдеуi көмегiмен атомның энергетикалық спектрiн есептеген кезде бұл факторларды ескеру мүмкін емес, өйткенi теңдеу салыстырмалық теорияны қанағаттандырмайды.

Сондықтан Шредингер теңдеуi көмегiмен атомның энергетикалық спектрiнiң нәзiк түзілiсiн бейнелеуге болмайды. Атомның энергетикалық спектрiн және оның нәзiк түзілiсiн арнайы салыстырмалылық теория талаптарын қанағаттандыратын Дирак теңдеуi көмегiмен дәл есептеп табуға болады. Бiрақ, басқаша жасауға да болады. Дирак теңдеуiн қолданбай-ақ, нәзiк түзілiс формуласын онша дәлме-дәл болмағанымен, қарапайым жолмен қорытып шығаруға болады. Сонда онша дәлме-дәл емес, бiрақ физикалық көрнекi амалды қолданып, сутегi атомының негiзгi күйлерiне жоғарыда аталған факторлардың әрқайсысы тудыратын энергетикалық түзетулер қарастырылады.

Релятивтiк эффектiң атомның энергетикалық күйлерiне әсерiн ең алғаш Зоммерфельд (1916) қарастырған. Е₀ энергетикалық деңгейiне релятивтiк энергетикалық түзету мына формуламен анықталады:

(1)

мұнда -нәзiк түзілiс тұрақтысы; -сутегi атомының релятивтiк эффектер ескерiлмегендегi энергиясы. Е_Р түзетуiнiң шамасы өте кiшi, реттiк шамасы ²Е₀10^-3эВ болады.

Е

57

ндi бiр валенттiк электроны бар атомдағы электрон энергиясына электрон спинiнiң әсерiн қарастырсақ. Меншiктi магниттiк моментi болуы арқасында электрон өзiн осы электронның орбиталық қозғалысы тудыратын магнит өрiсiнде орналастырылған «магниттiк диполь» сияқты көрсетедi. Атомдық физикада спиндiк магниттiк моменттiң орбиталық магнит өрiсiмен әсерлесуi спин-орбиталық әсерлесу (ls) деп аталады. Осы магниттiк әсерлесу нәтижесiнде электрон Е_s қосымша энергияға ие болады. Ендi спин-орбиталық әсерлесу энергиясын ескерейiк. Электрон ядроның электростатикалық өрiсiнде қозғалған кезде пайда болатын магнит өрiсiнiң кернеулiгi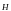 , ал -электронның меншiктi магниттiк моментi болсын дейiк. Сонда спин-орбиталық әсерлесу энергиясы Е_s мынаған тең

(2)

Электронның меншiктi магниттiк моментi:

(3)

, мұндағы (4)

(5)

-электронның меншiктi импульс моментi, ₀-Бор магнетоны, s-спиндiк кванттық сан (s=1/2).

Спин-орбиталық әсерлесудi бейнелеу үшін, және де атомдардың спектрлерiн жүйелеу үшін атомның векторлық моделi қолданылады. Осы модельде электронның-орбиталық қозғалысына сәйкес импульс моментi векторымен, ал оның спинi- векторымен берiледi. Спин-орбиталық әсерлесу арқасында электронның орбиталық моментi оның спиндiк моментiмен қосылады.

Қорытқы вектор = + электронның толық импульс моментiнiң векторы деп аталады.

; j-iшкi кванттық сан.

; -орбиталық кванттық сан.

Спин-орбиталық әсерлесу энергиясы үшін өрнек түрлендiру соңында мына түрге келедi

58

(6)

Атомдағы электронның энергиясын анықтағанда энергетикалық түзетуi релятивтiк түзетумен қатар ескерiлуi тиiс.

Сонымен, атом энергиясы мынаған тең:

(7)

Сонымен, екi фактордың екеуiнiң де әсер етуi нәтижесiнде бiр электронды атомның барлық деңгейлерi j кванттық санының мүмкін мәндерiнiң саны бойынша екi деңгейшеге жiктеледi. Осы жiктелу нәзiк немесе мультиплеттiк жiктелу деп аталады. Сондықтан жiктелу масштабын анықтайтын өлшемдiлiксiз  тұрақты-нәзiк түзілiс тұрақтысы деп аталады. Е_n бiр деңгейдiң j₁=+1/2 және j₂=-1/2 деңгейшелерi арасындағы энергия айырымы мынаған тең

(8)