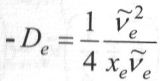28. Қарапайым Зееман эффекті.
Алдымен
нәзік түзілісі жоқ (синглет) спектрлік
сызықтардың зеемандық жіктелуін
қарастырайық. Мұнда сызықтар қарапайым
синглет деңгейлер (яғни толық спин S=0)
арасындағы кванттық ауысулар нәтижесінде
пайда болады. Осындай деңгейлер үшін
g=1. Демек ,
формула мына түрге келеді
өйткені S=0 болғандықтан, L=J,
болады,ал
1
-
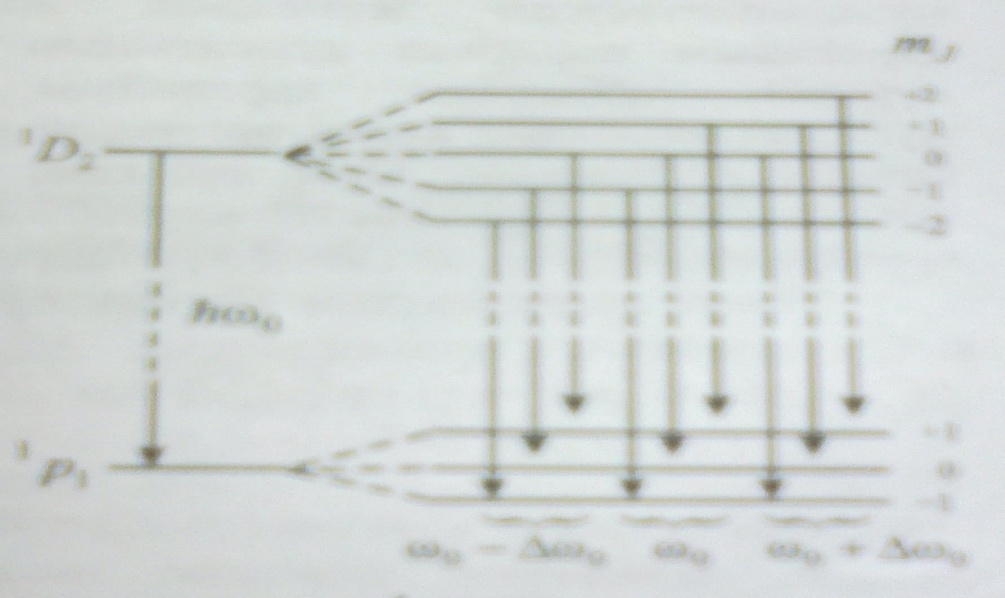
суретте L=1 және L=0күйлері арасындағы
ауысу (P→S) үшін,ал 2-суретте L=2 және
L=1 күйлері арасындағы ауысу (D→P) үшін
деңгейлердің және спектрлік сызықтардың
жіктелуі көрсетілген.
Магнит
өрісі жоқта жиілігі
жалғыз сызық байқалады. Өрісті қосқанда
,
сызықтан басқа ,бұған салыстырғанда
симметриялы орналасқан жиіліктері:
,
екі
сызық пайда болады.
31. Екі атомды молекуланың айналысы, айналыс спектрі.
Молекулалардың
ядролары қатаң бекiтiлген деп ұйғарып
айналыс спектрлерiн қарастырайық. Бұл
ротатор моделi, молекула құрамына кiретiн
массалары m
және
m
атомдар қайсыбiр осьтi айналып қозғала
алады. Атомдардың инерция моментi
бұлардың центрлерi арқылы өтетiн оське
қатысты I=r2-ге
тең, мұндағы
келтiрiлген масса, r-атомдардың
(ядролардың) ара қашықтығы.
Қатаң
ротатор моделi үшін молекуланың
энергетикалық күйлерi (
)
формуласымен бейнеленедi, бұған мына
айналыс термдерi сәйкес келедi
(9.5)
мұндағы
(9.6)
потенциалдық
энергия қисығының минимумына қатысты
айналыс тұрақтысы; Ie-инерция
моментi, гсм2;
-келтiрiлген
масса, re-ядроаралық қашықтық, см; J= 0, 1, 2,... айналыс кванттық саны.
Егер ∆Ее=0, ∆Еv=0 болса, молекуланың∆Еr айналыс энергиясы өзгермейтін болса, онда таза айналыс спектрі алынады. ∆Еr ~10-³--10-² эв, vr ~ 109-1011 Гц, j=1
С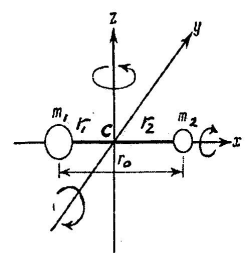
ұрыптау
ережесі
J
4
3
2
1
0
v
1-сурет
2B
Спектр 2В жиiлiгiнен басталып, 2В интервалымен жоғарырақ жиiлiктер жағына қарай жалғасады (1-сурет). Айналыс спектрiне тән жиiлiктер 109-1011с-1; бұларға сәйкес толқын ұзындық 0,01см (спектрдiң алыс инфрақызыл және микротолқындық аймақтары).
32.Екі атомды молекуланың тербелісі
Қарапайым гармоникалық осциллятор. Бірінші жуықтауда екі атомды молекула тербелістерін осциллятор көмегімен көрсетуге болады. Осындай гармоникалық осциллятордың (молекуланың) потенциалдық энергиясы
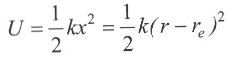(1)
болады.
Мұндағы күш тұрақтысы
к
осциллятордың
тербеліс жиілігімен былай байланысқан
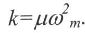
П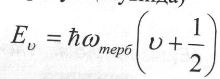
отенциалдық
энергия
үшін
(1) өрнекті
Шредингер
теңдеуіне
қойып
гармониялык
осциллятордың
энергия
деңгейлері
үшін
өрнекті
табамыз.
Екі атомды молекуланыц тербеліс энергиясы (гармоникалық осциллятор жуықтауында)
Тербеліс кванттық саны: ʋ= 0,1,2,...
Меншікті
тербелістер
жиілігі: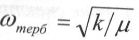
(к - квазисерпімді күш тұрақтысы, m - келтірілген масса).
Тербеліс энергиясы (см1):
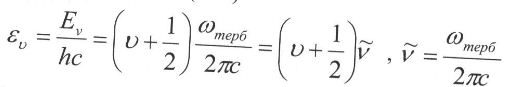
Кванттық ауысу энергиясы (см-1):
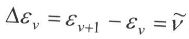
Тұрақты дипольдық моменті бар молекулалар ғана әр түрлі тербеліс деңгейлері арасында кванттық ауысу жолымен сәулені шығарып және жұта алады.
Гармоникалық осциллятордың тербеліс ауысулары үшін сұрыптау ережесі: ∆ʋ= ±1.
Гармоникалық осциллятордың энергетикалық диаграммасы және тербеліс спектрі (1 а-сурет).
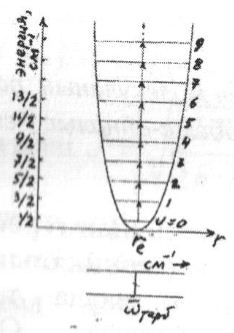
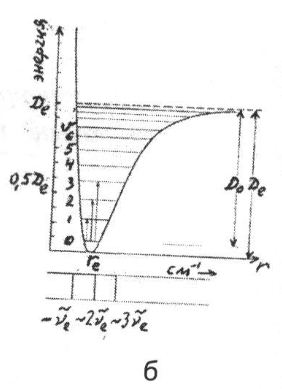
Ангармоникалық осциллятор (1б-сурет).
а)гармоникалық осциллятор жуықтауында екі атомды молекуланың потенциалдық энергиясы параболалық тәуелділік;
б)ангармоникалық осциллятордың потенциалдық энергиясы.
Екі атомды молекуланың тербеліс дeңгейлері (ангармоникалық осциллятор үшін) (см-1):
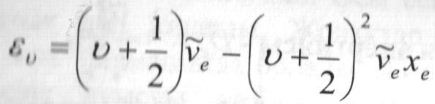
Ангармоникалық тұрақгы:xe˂0
Тербелістердің тепе теңдік жиілігі (см-1):ῦе - тепе-теңдік нүктесі маңайындағы шексіз кіші тербелістерінің жорамал жиілігі,
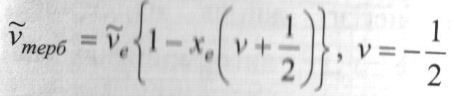болғанда
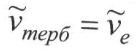болады.
Тербеліс кванттық саны өскенде ангармоникалық осциллятордың деңгейлері жақындаса түседі.
Ангармоникалық осциллятордың энергетикалық диаграммасы және тербеліс спектрі (1 б -сурет).
Ангармоникалық осциллятордың тербеліс ауысулары үшін сұрыптау ережелері: ∆ʋ = +1,±2,±3,.... үлкен∆ʋ өзгеріске сәйкес ауысулардың ықтималдығы аз болады.
Негізгі жұтылу жолағы ῦе - маңындағы жолақ, ʋ= 0 >ʋ=1,∆ʋ=+1 күшті ауысуға сәйкес келеді;
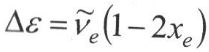
Бірінші
обeртон
- 2 ῦе
маңындағы
жолақ,
ʋ= 0 >ʋ=2,∆ʋ=+2 олсіз
ауысуға
сэйкес
келеді,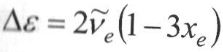
Екінші
обертон
- 3 ῦе
маңындағы
жолақ,
ʋ= 0 >ʋ=3,∆ʋ=+3 олсіз
ауысуға
сэйкес
келеді,
• Ыстық жолақтар - әлсіз жұтылу жолақтары. Мысалы,
ʋ= 0 >ʋ=2,∆ʋ=+2
бұлардың интенсивтігі зат үлгісінің температурасы өскенде өседі.
Диссоциация
энергиясы