7.Вероятность ошибки на выходе приемника.
При когерентном приёме сигналов ДЧМ на помехоустойчивость влияют только синфазные с сигналом составляющие помех x1 в фильтре 1 и x2 в фильтре 2. Эти составляющие имеют нормальный закон распределения амплитуд с одинаковыми дисперсиями
.
Вероятность превышения синфазной составляющей помехи в фильтре без сигнала x2 составляющей суммы сигнала и помехи в фильтре с сигналом (a + x1) равна
.
Для определения средней вероятности ошибки необходимо усреднить вероятность p(x2 > (a + x1)) по всем значениям случайной величины (a+x1), при этом для случая флуктуационной помехи (и симметричного канала связи) получим:
,
где h2 – отношение сигнал / шум.
h2 =Рс/Рп , где Рс- мощность сигнала Si, Рп –мощность помехи.
h2 = А2/2σ2 = (34*10-3)2/2*0,26*10-3 = 2,22 отсюда h = 1,49
Средняя вероятность ошибки равнa
pошЧМкг = 0,5 [ p(0 /1) + p(1/ 0)] = 0,5 [1 – Ф(h)] = 0,067.
Расчет зависимости РошАМ=f(h) для когерентного приема приведен в таблице 2 и показана на рисунке 5.
Таблица 2.
h |
0 |
1 |
1,49 |
2 |
2,5 |
3,5 |
3,5 |
Pош |
0,5 |
0,158 |
0,067 |
0,027 |
0,0062 |
0,00023 |
0,00023 |
Рис.5 Зависимость вероятности ошибки от соотношения сигнал шум
8.Выигрыш в отношении сигнал/шум при применении оптимального приемника.
При использовании в приёмнике оптимального фильтра вероятность ошибки определяется величиной отношения энергии элемента сигнала к спектральной плотности мощности помехи h02 = Eс / N0 = PсTс/ N0.
,
где
– энергия
элемента сигнала (∆fпрДЧМ-полоса
пропускания приемника),
N0 =σ2/∆fпрДЧМ – спектральная плотность помехи
N0 =σ2/∆fпрДЧМ=0,26*10-3/240000 = 1,08*10-9
Найдем h02
h0=2,4
Найдем энергетический выигрыш в соотношении сигнал/шум при использовании оптимального приемника, т.е. при оптимальной фильтрации принимаемого сигнала:
h0/h=2,4/1,49 = 1,61
Т
аким
образом, при оптимальной фильтрации
соотношение сигнал/шум увеличивается
в 1,61 раз.
9.Максимально возможная помехоустойчивость при заданном виде сигнала.
Котельников разработал теорию потенциальной помехоустойчивости. Он доказал, что для данного вида модуляции и данного вида помехи приемник обладает предельной помехоустойчивостью, превзойти которую нельзя. Эта помехоустойчивость называется потенциальной помехоустойчивостью. Потенциальная помехоустойчивость, на что впервые обратил внимание Котельников, зависит только от так называемой эквивалентной энергии сигналов. Помехоустойчивость выше (вероятность ошибки меньше) у той системы, у которой больше эквивалентная энергия используемых сигналов. Для определения такой возможной помехоустойчивости приема сигналов, определим среднюю вероятность ошибки при оптимальном приеме для ДЧМ сигнала:
pошЧМкг = 0,5 [1 – Ф(h0)] = 0,067
10. Принятие решения приемником по трем независимым отсчетам.
Для повышения помехоустойчивости приёма дискретных двоичных сообщений, решение о переданном символе принимается не по одному отсчёту на длительности элемента сигнала 0 t T, а по трем некоррелированным отсчётам z(t1)=9*10-3 ,z(t2)=5,4*10-3, z(t3)=9,9*10-3 принимаемой смеси сигнала и помехи. Данный метод называется методом дискретного накопления. Для принятия решения о переданном символе, должна быть определена совместная трехмерная плотность распределения вероятностей для заданных трех отсчётов, т. е. W3 (Z /1) и W3(Z /0). Для случая гауссовского стационарного шума некоррелированные отсчёты смеси сигнала и шума будут независимыми. Следовательно, трехмерная плотность распределения вероятности будет равна произведению одномерных плотностей распределения каждого из отсчётов, т.е.
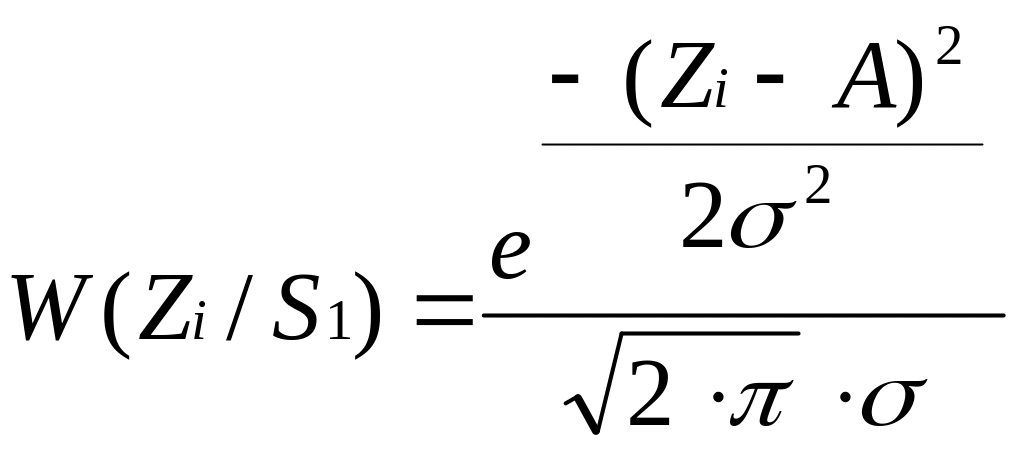
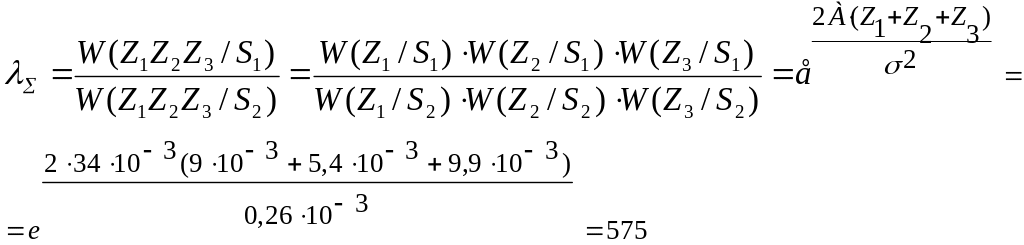
0=0,33
Так как,>0 то в нашем случае принимается S1.