5. Структурная схема приемника.

В соответствии с исходными данными варианта в качестве приемника применяется приемник когерентного приема ДЧМ. При ДЧМ: при передачи “1” передается колебание с одной частотой, а при “0” с другой, при этом на приеме все параметры передаваемого сигнала известны. Задачей приемного устройства является определение степени соответствия поступивших сигналов с эталонными на фоне помех.

Элементами сигнала при ЧМ являются:

, где i=1,2;  флуктуационная помеха типа гауссовского шума.

Векторная диаграмма.

S 1(t)=Acos 1t

S 2(t)=Acos 2t S2(t)

Вычисление степени соответствия математически записывается следующим образом:

где t – время наблюдения за сигналом,

S1(t), S2(t)- эталонные сигналы

Z(t) – принятый сигнал с помехой

Если Z(t) ближе к одному из эталонных сигналов, то вычисленное значение будет ближе к нулю, таким образом можно записать математическую запись алгоритма принятия решения.

Если на передаче S1(t) и , то приемник принимает решение в пользу S1(t) – алгоритм идеального приемника Котельникова. Если же на передаче S2(t) и , то приемник принимает решение в пользу S2(t).

Раскрыв скобки в математической записи алгоритма принятия решения получим:

в результате приведения подобных получим:

или В_S1 < В_S2

В_Si – функция корреляции, устройство вычисляющее функцию корреляции называют активным фильтром или коррелятором.

На основе последней формулы можно составить схему приемника ДЧМ (рис.3)

Рис.3 Схема приемника ДЧМ

Схема содержит два перемножителя по числу передаваемых сигналов, два коррелятора (активных фильтра) и решающее устройство (РУ).При приеме сигналов ДЧМ местные генераторы генерируют эталонные сигналы S1(t)=Acos ₁t и S2(t)=Acos ₂t.

В перемножителях поступившие и эталонные сигналы перемножаются. Далее сигналы поступают на коррелятор. Мгновенные значения с выходов интегратора в определенные моменты времени (например, в середине посылки) сравнивается в РУ с некоторым пороговым уровнем U_порог.. При выполнении неравенства В_S1 > U_порог регистрируется сигнал S1, в противном случае — S2.

6.Принятие решения приемником по одному отсчету

Сообщения передаются последовательностью двоичных символов "1" и "0", которые появляются с априорными вероятностями соответственно p(1) и р(0). Этим символам соответствуют канальные сигналы S₁(t) и S₂(t), которые точно известны в месте приема.

В канале связи на передаваемые сигналы воздействует гауссовский стационарный шум с дисперсией ². Приемник, оптимальный по критерию идеального наблюдателя, принимает решение по одному отсчету смеси сигнала и помехи

Z(t₀) = S_i (t₀ )+ ς(t₀)

на интервале элемента сигнала длительности Т.

Критерий минимального среднего риска минимизирует среднюю вероятность ошибки

p_ош = P(S₁)P(х₂/S₁) + P(S₂)P(х₁/S₂)

Если бы на входе приемника отсутствовали помехи, мы имели бы дело с "чистыми" сигналами S₁ и S₂ и задача разделения сигналов была бы очень проста. При наличии же помех сигналы искажаются и для их описания приходится использовать вероятностное пространство. Сами сигналы вместе с помехами описываются уже функциями плотности вероятности w(x/S₁) и w(x/S₂), которые изображены на рис.4 . На этом же рисунке показан порог х_п.

Рис.4

Заштрихованная часть рисунка левее х_п имеет площадь, равную

Р(S₂)w(x/S₂)dx = Р(S₂)P(x/S₂),

а заштрихованная часть правее х_п имеет площадь, равную

Р(S₁)w(x/S₁)dx = Р(S₁)P(x/S₁),

Сумма этих величин, в соответствии с формулой , есть средний риск R_ср. Из рис. 4. видно, что R_ср будет минимальным, когда минимальна суммарная площадь под кривыми. Это будет в том случае, если величина х_п соответствует точке пересечения кривых на рис. . Следовательно, условием получения min{R_ср} является такой порог х_п, при котором наступает равенство ординат приведенных кривых, т. е.

Р(S₁)w(x/S₁)dx = Р(S₂)w(x/S₂),

откуда получаем следующее соотношение:

.

Стоящее слева выражение называется отношением правдоподобия

(х) = ,

Рассчитаем отношение правдоподобия для по исходным данным:

, где

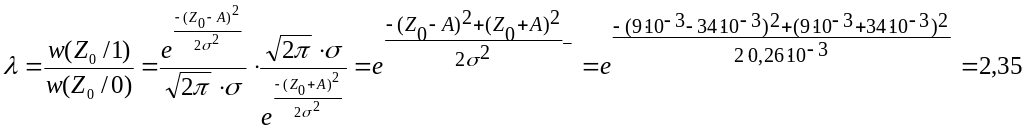
Приемник, использующий отношение правдоподобия сравнивает величин (х) с ₀, (пороговое отношение правдоподобия), если (х) > ₀, приемник выдает сигнал S₁, в противном случае сигнал S₂. Пороговое отношение правдоподобия определяется по формуле:

₀= . Следовательно приемник притмет сигнал S₁.

Рассчитаем и построим функции распределения плотности вероятности для W(ς), W(z/0) и W(z/1).

; ; ;

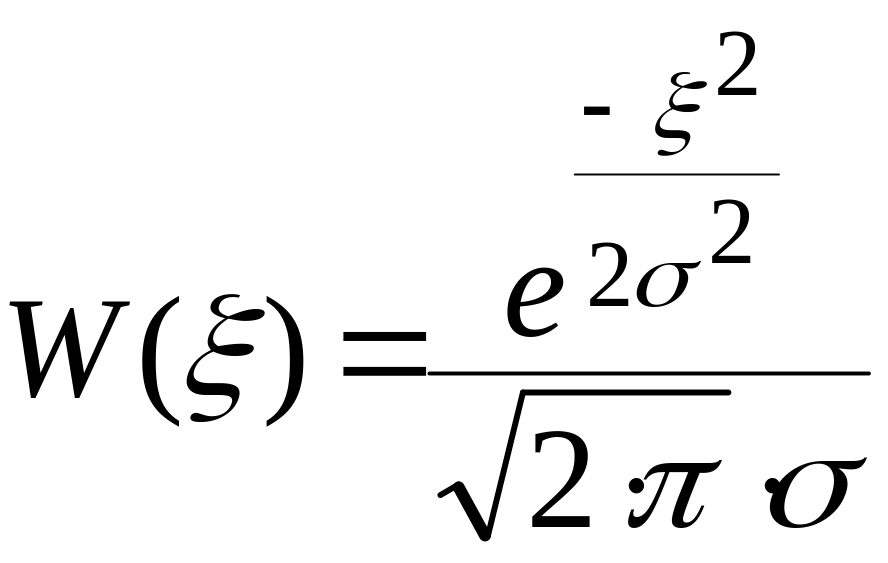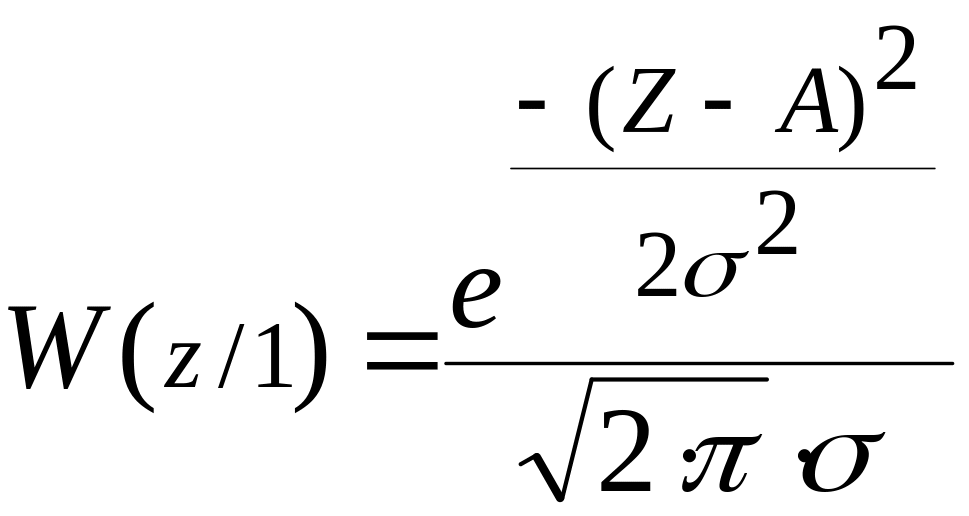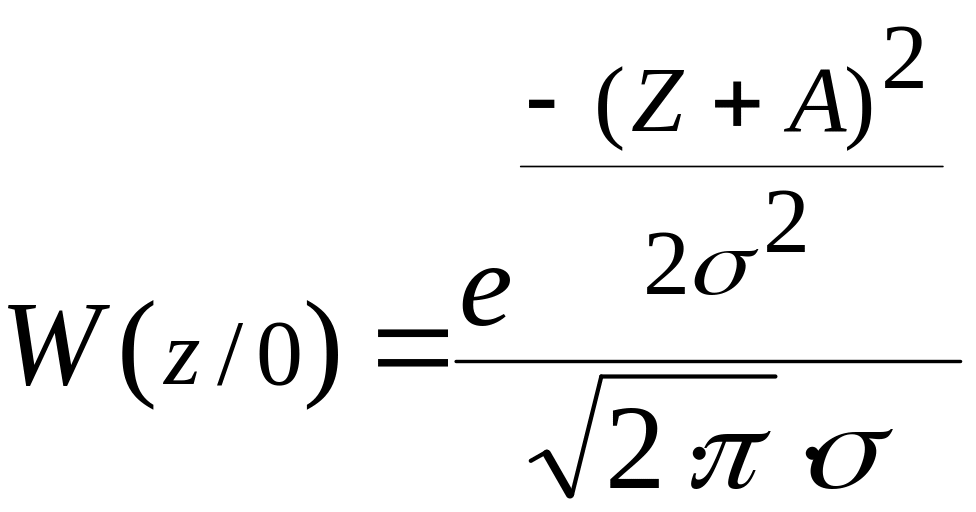Результаты расчета приведены в таблице 1

Таблица 1.

Z, мВ	-12	-10	-8	-6	-4	-2	-1	0	1	2	4	6	8	10	12
W(ς)	6,1	13,2	24,9	40,8	58	71,7	75,6	76,9	75,6	71,7	58	40,8	24,9	13,2	6,1
W(z/1)	0,0027	0,014	0,062	0,24	0,8	2,33	3,76	5,86	8,8	12,77	24,17	39,69	56,57	69,97	75,11
W(z/0)	75,11	69,97	56,57	39,69	24,17	12,77	8,8	5,86	3,76	2,33	0,8	0,24	0,062	0,014	0,0027