27 Нормальний закон.
Випадкова величина
Х
називається розподіленою за нормальним
законом з параметрами
і
,
якщо її щільність розподілу
,
.
Функція розподілу
має вигляд 
.
Якщо зробити заміну
то 
,
де
- функція Лапласа.
;
якщо
то
,
але
.
Ймовірність
того, що нормально розподілена випадкова
величина набуде значення з інтервалу
,
обчислюється за формулою
=
.
Обчислимо математичне
сподівання
.
Зробивши заміну
,
,
;
отримаємо
=
+
.
Інтеграл
=
( це інтеграл Пуассона), інтеграл
=0,
як інтеграл від непарної функції. Отже,
.
(22)
Обчислимо
дисперсію
.
Заміна
зводить інтеграл до такого
,
який інтегруємо частинами
+
=
.
Таким чином,
.
(23)
Отже, ми вияснили ймовірнісний зміст параметрів нормального розподілу
- це математичне сподівання нормально розподіленої випадкової величини, а
- її середнє квадратичне відхилення.
28
Известно,
что если случайная величина X задана
плотностью распределения 
,
то вероятность того, что X примет
значение, принадлежащее интервалу
(a,b), такова:
.
Пусть случайная величина X распределена по нормальному закону. Тогда
.
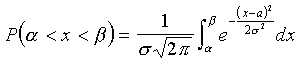Преобразуем
эту формулу так, чтобы можно было
пользоваться готовыми таблицами. Введем
новую переменную 
.
Отсюда 
.
Найдем
новые пределы интегрирования. Если 
,
то 
,
если 
,
то 
.
Тогда
.
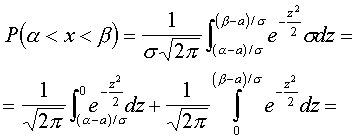
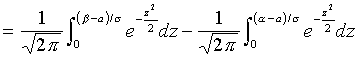Выражение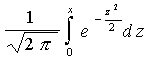 
,
входящее в эту формулу, является функцией
верхнего предела X, которая называется
функцией Лапласа или интегралом
вероятностей и обозначается Ф(x). В
результате получаем:
Ф
—
Ф
,
где
Ф(x) = 
.
Эту формулу называют формулой Лапласа.
Если
случайная величина X является признаком
генеральной совокупности, то формула
Лапласа дает долю элементов генеральной
совокупности, у которых значение признака
X находится в границах от 
до 
.
Интеграл,
через который выражается функция
Лапласа, нельзя выразить через элементарные
функции. Его можно представить в виде
степенного ряда, если разложить в ряд
подынтегральную функцию
и
почленно проинтегрировать ряд. Тогда
Ф(x) = 
.
C помощью этого ряда можно вычислить значение Ф(x) для любого x с любой точностью. Составлены специальные таблицы значений функции Лапласа.
Отметим ряд свойств функции Лапласа, полезных для применения.
1. Функция Ф(x) – нечетная, т. е. Ф(-x) = –Ф(x).
2. Функция
Ф(x) – возрастающая, быстро приближающаяся
к своему пределу, равному 0,5: Ф(0) = 0,
Ф(1) = 0,3413, Ф(2) = 0,4772, Ф(3) = 0,4986,
Ф(4) = 0,4999 и т.д. На практике полагают
Ф(x) 
для
x>5.
29 Правило трёх сигм
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется правилом трех сигм.
Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.