23 (Биномиальное распределение ).

Используем свойство устойчивости биномиального распределения относительно суммирования. Возьмём на каком-нибудь вероятностном пространстве   независимых случайных величин   с распределением Бернулли  . Тогда их сумма   имеет распределение  , и по свойству (E4) имеем:

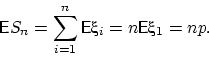
А поскольку   независимы, и дисперсия каждой равна  , то

Итак,  ,   для  .

24 Диференціальна функція розподілу

Виникає питання: яким чином, спостерігаючи випадкові значення Х, побудувати функцію розподілу  . Виявляється, що до цієї функції практично простіше підходити через іншу функцію.

Нехай   - неперервна і диференційована функція розподілу випадкової величини Х. Підрахуємо ймовірність попадання значень на інтервал  , а саме:

.

Поділимо цю рівність на   і перейдемо до границі при умові  :

      (3)

Отримана похідна   називається густиною (щільністю) розподілу випадкової величини Х, або диференціальною функцією розподілу. В літературі часто її позначають  . Зміст густини розподілу полягає в тому, що вона вказує, як часто появляється випадкова величина Х в деякому околі точки х при повторенні випробувань.

Ймовірність попадання неперервної випадкової величини на інтервал   рівна

.

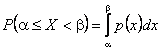Дійсно  ,  ,  .

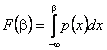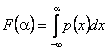Тому:

.

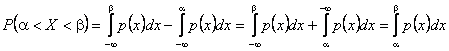25 Закон розподілу ймовірностей можна подати ще в одній формі, яка придатна і для дискретних, і для неперервних випадкових величин, а саме: як функцію розподілу ймовірностей випадкової величиниF(х), так звану інтегральну функцію. Функцію аргументу х, що визначає ймовірність випадкової події Х < x, називають функцією розподілу ймовірностей: F(x) = P(X < x) (62) Цю функцію можна тлумачити так: унаслідок експерименту випадкова величина може набути значення, меншого за х . Наприклад, F(5) = P(X < 5) означає, що в результаті експерименту випадкова величина Х (дискретна чи неперервна) може набути значення, яке міститься ліворуч від х = 5, що ілюструє рис. 21. Рис. 21 Розглянемо властивості F(x): 1.  Ця властивість випливає з означення функції розподілу. 2.   є неспадною функцією, а саме  , якщо  . ! Доведення. Позначимо відповідно А, В, С події (Х < x₂), (Х < x₁) і  . 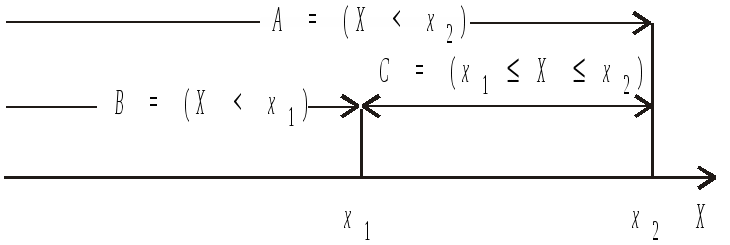Випадкові події В і С є несумісними (А С = ) (рис. 22). Рис. 22

26 Найбільш повна характеристика випадкової величини дається її функцією розподілу (або також і щільністю розподілу для неперервної випадкової величини). Проте досить часто доцільно обмежитися простішою, хоч і неповною інформацією про випадкову величину. Наприклад, досить вказати окремі числові величини, які певним чином визначають істотні риси розподілу випадкової величини: деяке середнє значення випадкової величини; деяке число, що характеризує ступінь розсіювання значень випадкової величини навколо її середнього значення, тощо. Користуючись такими характеристиками, ми в стислій формі можемо отримати інформацію про істотні особливості законів розподілу випадкової величини. Характеристики, що виражають в стислій формі найістотніші особливості закону розподілу випадкової величини, називаються числовими характеристиками випадкової величини. До них в першу чергу відносяться математичне сподівання і дисперсія.

Математическое ожидание 

     Дисперсия