
- •Перестановки без повторений Перестановки в ряд
- •Перестановки с повторениями
- •Размещения без повторений
- •Свойства бинома Ньютона
- •За індукції
- •Класичне означення ймовірності.
- •9. Теорема про ймовірність суми двох несумісних подій
- •1. Залежні та незалежні випадкові події
- •Незалежні події
- •2. Умовна ймовірність та її властивість
- •Властивостi
- •21 Закон распределения дискретной случайной величины
- •Числовые характеристики дискретных случайных величин
- •23 (Биномиальное распределение ).
- •24 Диференціальна функція розподілу
- •27 Нормальний закон.
- •29 Правило трёх сигм
- •30. Поняття про закон великих чисел. Нерівності Чебишева
- •31. Мода та медіана, квантилі
- •32. Рівномірний розподіл та його числові характеристики Рівномірний розподіл на відрізку [c,d]
- •33. Показниковий розподіл та його числові характеристики
- •34. Розподіл Пуассона та його числові характеристики
- •35. Геометричний розподіл та його числові характеристики
- •36. Початкові та центральні моменти. Асиметрія та ексцес
- •38. Теорема Чебишова
- •39. Теорема Бернуллі
- •43 Марківські випадкові процеси
- •46 Вибіркові характеристики.
46 Вибіркові характеристики.
При статистичних дослідженнях вибірки важливим етапом є оцінювання її числових характеристик, які називають вибірковими характеристиками.
Розмах вибірки R — це різниця між найбільшим і найменшим значенням випадкової величини у вибірці.
Для вибірки, розглянутої в прикладі 1 попереднього пункту, маємо R = 12 - 1 = 11.
Мода вибірки МO — те значення випадкової величини, що зустрічається у вибірці найчастіше.
Для вибірки, розглянутої в прикладі 1 попереднього пункту є дві моди — це числа 7 і 8. Можна записати МO1 = 7; МO2 = 8.
Медіана вибірки Ме — серединне значення ранжованої вибірки.
Медіана ділить ранжовану вибірку на дві рівні за кількістю частини. Якщо у вибірці непарна кількість випадкових величин, то його медіаною є число, яке стоїть посередині.
Наприклад, у ранжованій вибірці:
![]()
що складається з 7 випадкових величин, медіаною є число 3. Можна записати Ме = 3.
Якщо у вибірці парне число випадкових величин, то медіана — середнє арифметичне двох чисел, що стоять посередині.
Наприклад, у ранжованій вибірці:
![]()
що
складається з 8 випадкових величин,
медіана — це середнє арифметичне чисел
4 і 5, що стоять посередині ряду. Отже, Ме
= (4 + 5)/2.
Середнє
арифметичне вибірки
![]() —
це середнє арифметичне всіх її значень
x1;
x2;
x3;…;
xn.
—
це середнє арифметичне всіх її значень
x1;
x2;
x3;…;
xn.
Так, наприклад, середнє арифметичне вибірки, розглянутою у прикладі 1 попереднього пункту знаходиться наступним чином:

Варіаційним рядом (або генеральною сукупністю), побудованим за вибіркою X1, X2, ..., XN, називають послідовність xi, розміщених у порядку зростання: X[1]≤ X[2]≤...≤X[N]. Варіаційний ряд - упорядкована за величиною послідовність вибіркових значень спостережуваної випадкової величини рівні між собою елементи вибірки нумеруються в довільному порядку; елементи варіаційного ряду називаються порядковими (ранговими) статистиками; число λm = m / n називається рангом порядкової статистикиВаріаційний ряд використовується для побудови емпіричної функції розподілу
Гістогра́ма (від грец. histos, тут стовп + gramma — межа, буква, написання) — спосіб графічного представлення табличних даних. Являє собою діаграму, що складається з прямокутників без розривів між ними
Горизонтальні
межі прямокутника — інтервал
групування статистичного
ряду.
Нижня межа прямокутника розміщена на
осі 0x, а висота задається формулою
![]() ,
де
,
де
![]() —
значення даного інтервалу статистичного
ряду,
—
кількість інтервалів, а
—
значення даного інтервалу статистичного
ряду,
—
кількість інтервалів, а
![]() —
його ширина.[Джерело?]
—
його ширина.[Джерело?]
При
![]() гістограма
прямує до графіка
щільності.
гістограма
прямує до графіка
щільності.
Найчастіше,
для зручності беруть рівномірне розбиття
статистичного ряду, тобто однакові
розміри інтервалів
![]() .
.
Таким чином, гістограма є графічним зображенням залежності частоти попадання елементів вибірки від відповідного інтервалу групування.
47 Полігон частот (в математичній статистиці) - один із способів графічного представлення щільності ймовірності випадкової величини. Являє собою ламану, що сполучає точки, відповідні серединним значенням інтервалів угрупування і частотам цих інтервалів.
Статистична оцінка - це один із двох типів статистичного . Вона являє собою особливого роду метод судження про числові значення характеристик (параметрів) розподілу генеральної сукупності за даними вибірки з цієї сукупності. Тобто, маючи результати вибіркового спостереження, ми намагаємося оцінити (з найбільшою точністю) значення визначених параметрів, від яких залежить розподіл ознаки (змінної), яка нас цікавить, у генеральній сукупності.
Інтервальною
оцінкою параметру g
називається інтервал, межі якого l1
та l2
являють
собою функції значень вибірки
![]() і
який з заданою ймовірністю Р
накриває оцінюваний параметр:
і
який з заданою ймовірністю Р
накриває оцінюваний параметр:
![]() (2.3)
(2.3)
Інтервал
![]() називається
довірчим, а його межі l1
та l2
-
випадкові величини – нижня та верхня
довірчі межі відповідно. Р
називається
довірчою ймовірністю, а величина α=1-P
-
рівнем значимості, який використовується
при побудові довірчого інтервалу. Таким
чином інтервальна оцінка характеризується
шириною довірчого інтервалу L=l2-l1
та довірчою ймовірністю Р,
яка характеризує степінь надійності
результатів.
називається
довірчим, а його межі l1
та l2
-
випадкові величини – нижня та верхня
довірчі межі відповідно. Р
називається
довірчою ймовірністю, а величина α=1-P
-
рівнем значимості, який використовується
при побудові довірчого інтервалу. Таким
чином інтервальна оцінка характеризується
шириною довірчого інтервалу L=l2-l1
та довірчою ймовірністю Р,
яка характеризує степінь надійності
результатів.
Процедура отримання інтервальної оцінки полягає в наступному:
Записуємо певне ймовірнісне твердження виду
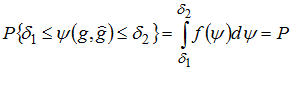 (2.4)
(2.4)
де () – функція густини ймовірності випадкової величини . При цьому значення 1 та 2 визначаються за допомогою додаткових умов:
![]() (2.5)
(2.5)
Аргумент виразу (2.4) перетворюють таким чином, щоби в результаті параметр, який оцінюється, виявився між величинами, визначеними за вибіркою. Це й будуть межі довірчого інтервалу (l1, l2). Функція
 обирається
таким чином, щоб вона дозволяла подібне
перетворення та мала відому (краще
табульовану) функцію густини ймовірності
f(),
що суттєво полегшує визначення 1
та
2.
обирається
таким чином, щоб вона дозволяла подібне
перетворення та мала відому (краще
табульовану) функцію густини ймовірності
f(),
що суттєво полегшує визначення 1
та
2.
48 Вибіркове (емпіричне) середнє значення — характеристика положення для вибіркового розподілу. [1]
Означення
Нехай
![]() —
випадкова вибірка.
—
випадкова вибірка.
Вибірковим середнім називається середнє арифметичне елементів даної вибірки:[2]
![]() .
.
Властивості вибіркового середнього
Нехай
 —
функція
вибіркового розподілу.
Тоді для будь-якого фіксованого
—
функція
вибіркового розподілу.
Тоді для будь-якого фіксованого
 функція
функція
 є
(невипадковою) функцією дискретного
розподілу.
є
(невипадковою) функцією дискретного
розподілу.
Вибіркове середнє — незміщена оцінка теоретичного середнього значення:
 .
.
Вибіркове середнє — строго конзистентна оцінка теоретичного середнього:
 майже
напевне
при
.
майже
напевне
при
.
Вибіркове середнє — асимтотично нормальна оцінка. Нехай дисперсія випадкових величин скінченна і ненульова, тобто
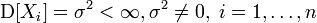 .
Тоді
.
Тоді
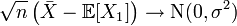 за
розподілом при
,
де
за
розподілом при
,
де
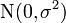 —
нормальний
розподіл
з середнім
—
нормальний
розподіл
з середнім
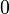 і
дисперсією
і
дисперсією
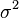 .
.
Вибіркове середнє з нормальної вибірки — ефективна оцінка її середнього.
Вибіркові дисперсії s2, S2 — це числові характеристики розсіювання значень випадкової вибірки, що являє собою сукупність результатів незалежних спостережень. Визначаються в звичайних сукупностях вимірів. У теорії точності вимірювань їх ще називають дисперсіями вимірів, або просто дисперсіями.
Є випадкова
вибірка
![]() обсягу
n.
обсягу
n.
Вибірковою дисперсією s2 називається половина середнього квадрата
 відхилень
значень вибірки:[1]
відхилень
значень вибірки:[1]
![]() .
.
Вибірковою дисперсією S2 називається половина середнього квадрата
 різниць
значень вибірки:[2]
різниць
значень вибірки:[2]
![]() .
.
Інтервальні оцінки параметрів розподілу. Інтервального називають оцінку, яка визначається двома числами-кінцями інтервалу. Інтервальні оцінки дозволяють встановити точність і надійність оцінок. Нехай знайдена за даними вибірки статистична характеристика Q * служить оцінкою невідомого параметра Q. Будемо вважати Q постійним числом (Q може бути і випадковою величиною). Ясно, що Q * тим точніше визначає параметр Q, чим менше абсолютна величина різниці | Q-Q * |. Іншими словами, якщо d> 0 і | Q-Q * | <d, то чим менше d, тим оцінка точніше. Таким чином, позитивне число d характеризує точність оцінки. Проте статистичні методи не дозволяють категорично стверджувати, що оцінка Q * задовольняє нерівності | Q-Q * | <d; можна лише говорити про ймовірність g, з якою це нерівність здійснюється. Надійністю (довірчою ймовірністю) оцінки називають імовірність g, з якою здійснюється нерівність | Q-Q * | <d. Зазвичай надійність оцінки задається наперед, причому в якості g беруть число, близьке до одиниці. Найбільш часто задають надійність, рівну 0,95; 0,99 і 0,999. Нехай імовірність того, що, | Q-Q * | <d дорівнює g: P (| Q-Q * | <d) = g. Замінивши нерівність рівносильним йому подвійним нерівністю отримаємо: Р [Q *-d <Q <Q * + d] = g Це співвідношення слід розуміти так: вірогідність того, що інтервал Q * - d <Q <Q * + d містить в собі (покриває) невідомий параметр Q, дорівнює g. Інтервал (Q * - d Q * + d) називається довірчим інтервалом, який покриває невідомий параметр з надійністю g. 49 Надійні інтервали для оцінки математичного сподівання нормального розподілу при відомому
 .
Нехай
відомо, що випадкова величина Х
розподілена нормально і
-
її середнє квадратичне відхилення.
Потрібно побудувати інтервальну оцінку
для невідомого математичного сподівання
.
Нехай
відомо, що випадкова величина Х
розподілена нормально і
-
її середнє квадратичне відхилення.
Потрібно побудувати інтервальну оцінку
для невідомого математичного сподівання
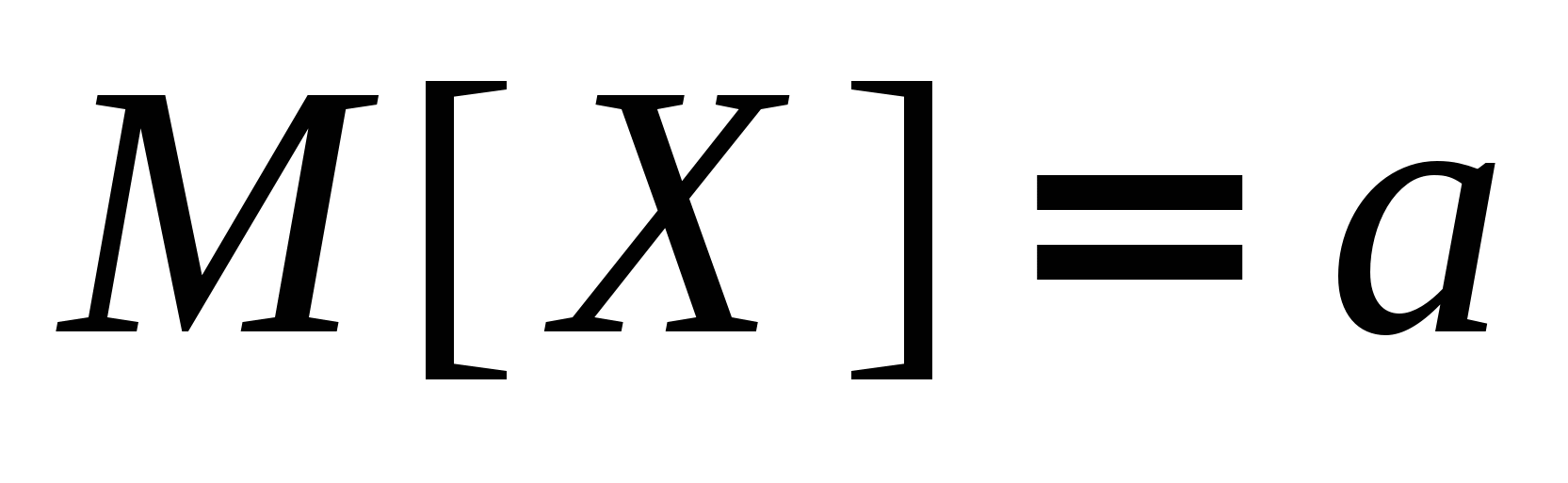 .
Точковою оцінкою для математичного
сподівання є вибіркове середнє
.
Точковою оцінкою для математичного
сподівання є вибіркове середнє
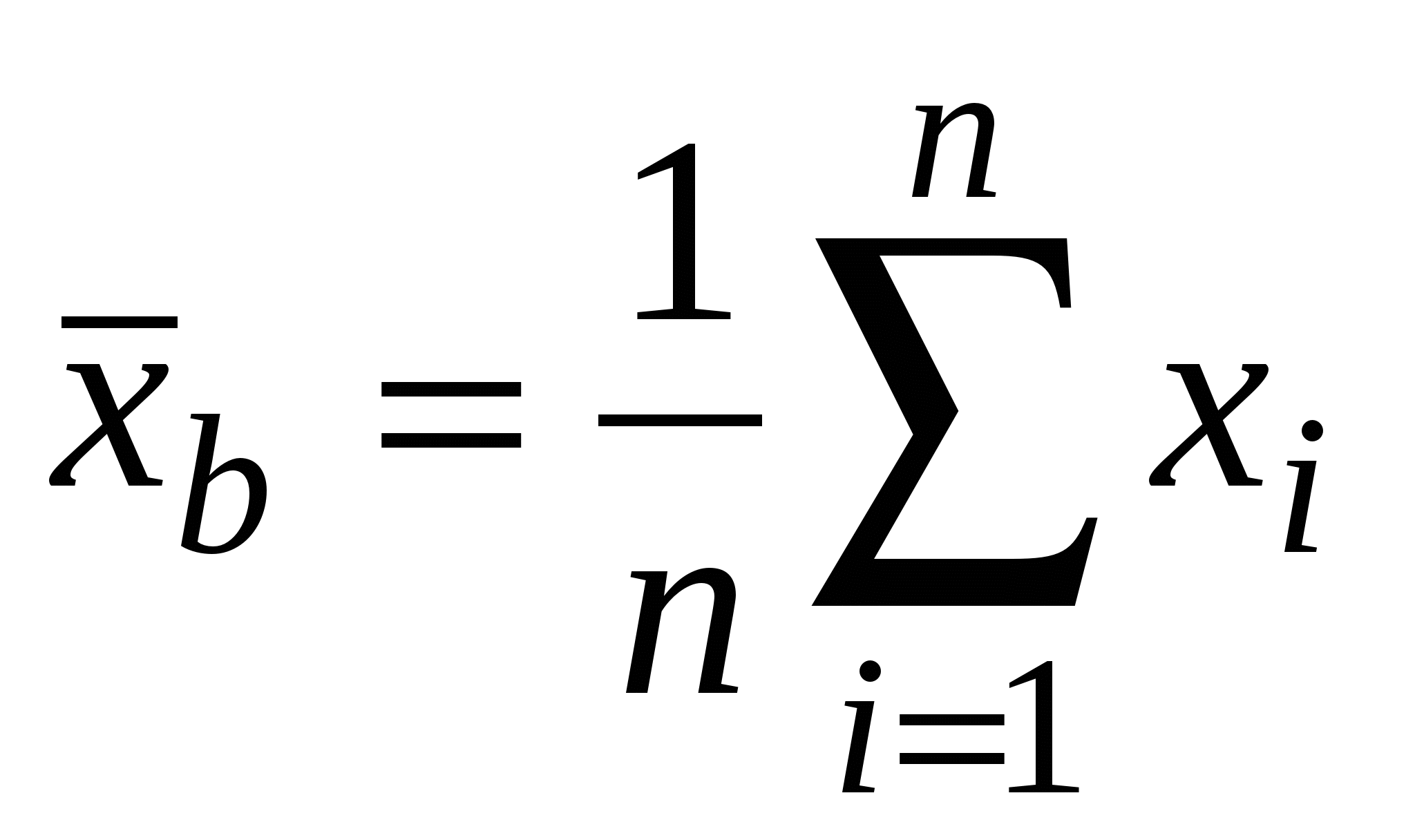 .
(5) Середнє вибіркове
.
(5) Середнє вибіркове
 є
різним для окремо взятих вибірок з
генеральної сукупності, отже його можна
розглядати як випадкову величину
є
різним для окремо взятих вибірок з
генеральної сукупності, отже його можна
розглядати як випадкову величину
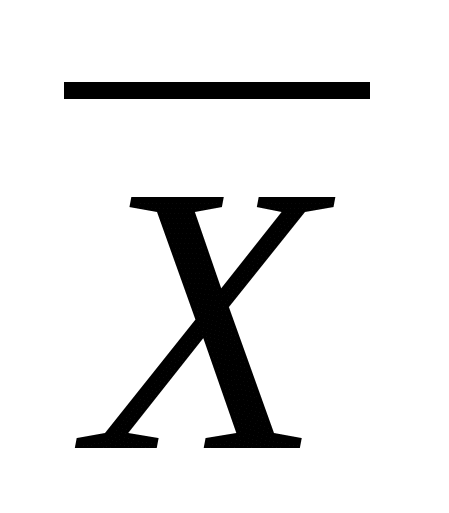 ,
а значення
,
а значення
 як
однаково розподілені незалежні випадкові
величини
як
однаково розподілені незалежні випадкові
величини
 (
(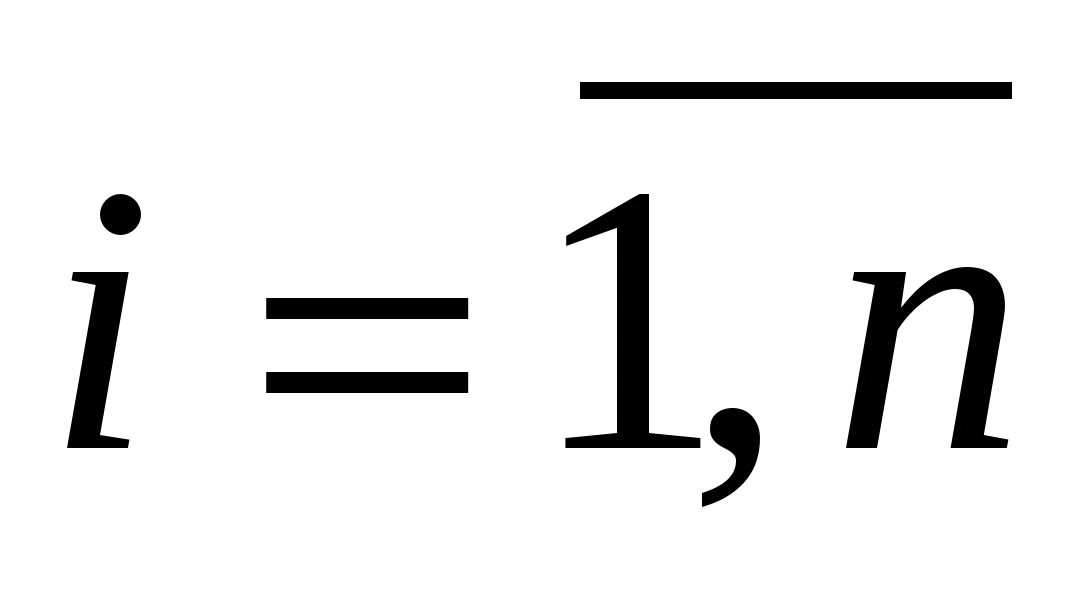 ).
Оскільки значення
).
Оскільки значення
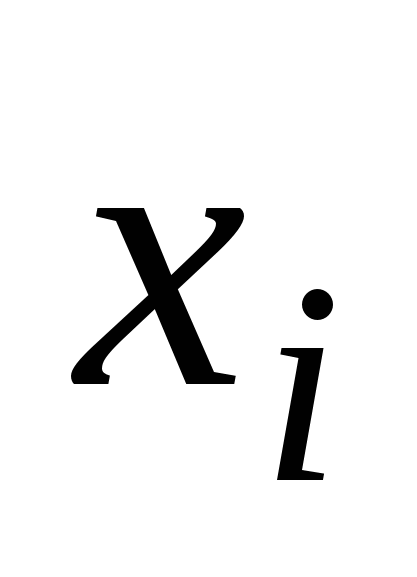 незалежні,
то
незалежні,
то
 ,
,
 ,
Вважаємо,
що
,
Вважаємо,
що
 -
відома величина.
Нерівність
-
відома величина.
Нерівність
 (6)
повинна
виконуватись із заданою ймовірністю
(6)
повинна
виконуватись із заданою ймовірністю

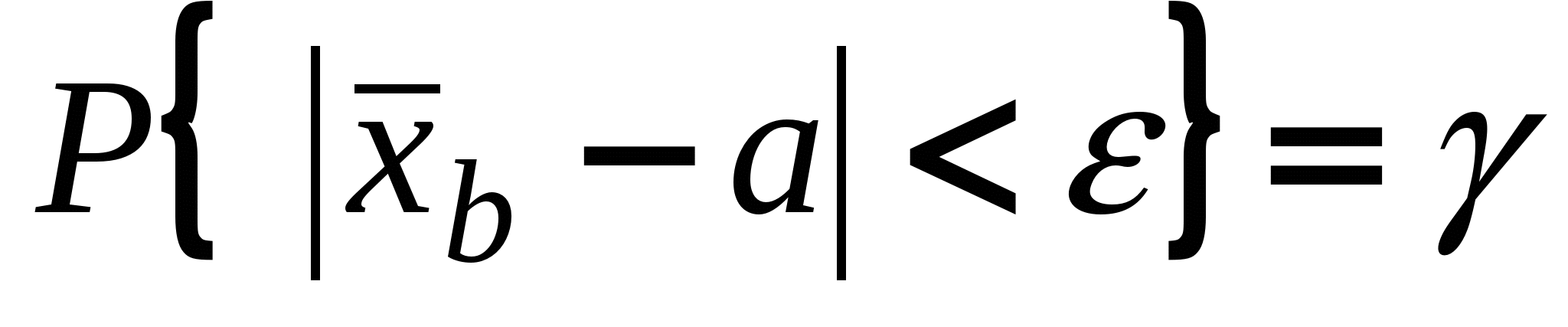 або,
замінивши нерівність (6) еквівалентною
нерівністю, отримаємо
або,
замінивши нерівність (6) еквівалентною
нерівністю, отримаємо
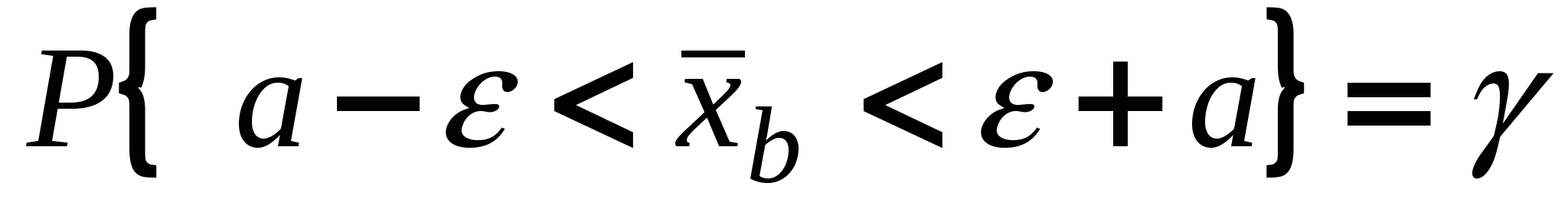 ,
(7)
Пригадаємо, що для нормально
розподіленої випадкової величини Х
з параметрами а
і
ймовірність
попадання в інтервал
,
(7)
Пригадаємо, що для нормально
розподіленої випадкової величини Х
з параметрами а
і
ймовірність
попадання в інтервал
 визначається
формулою
визначається
формулою
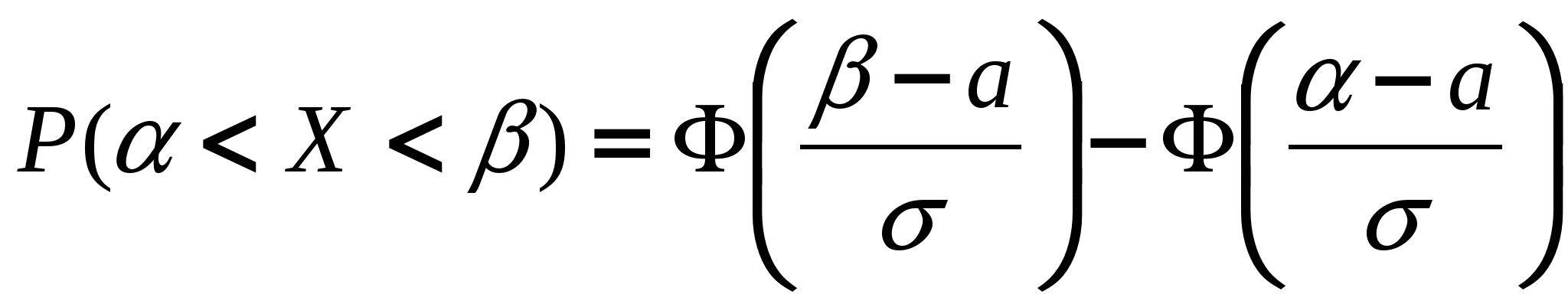 де
де
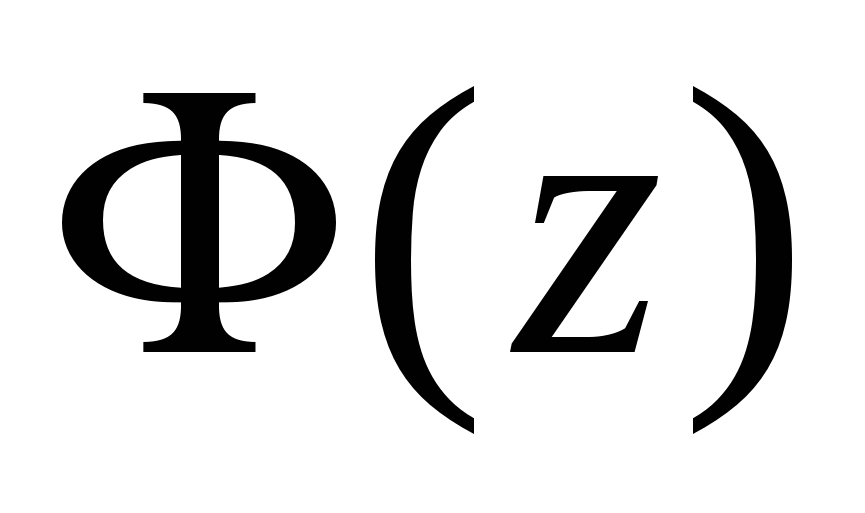 -
функція Лапласа (табульована).
Тоді
співвідношення (7) можна переписати
так
-
функція Лапласа (табульована).
Тоді
співвідношення (7) можна переписати
так
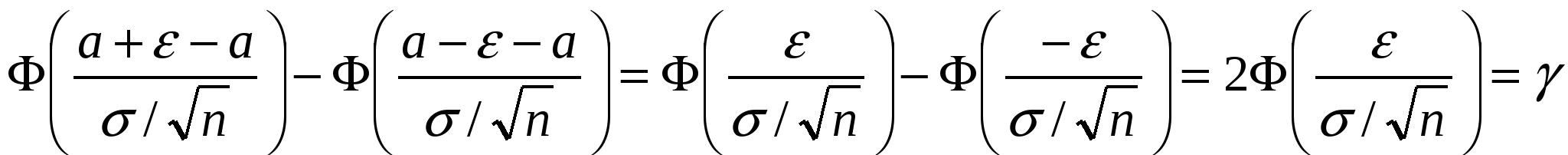 .
Позначивши
.
Позначивши
 ,
маємо рівняння
,
маємо рівняння
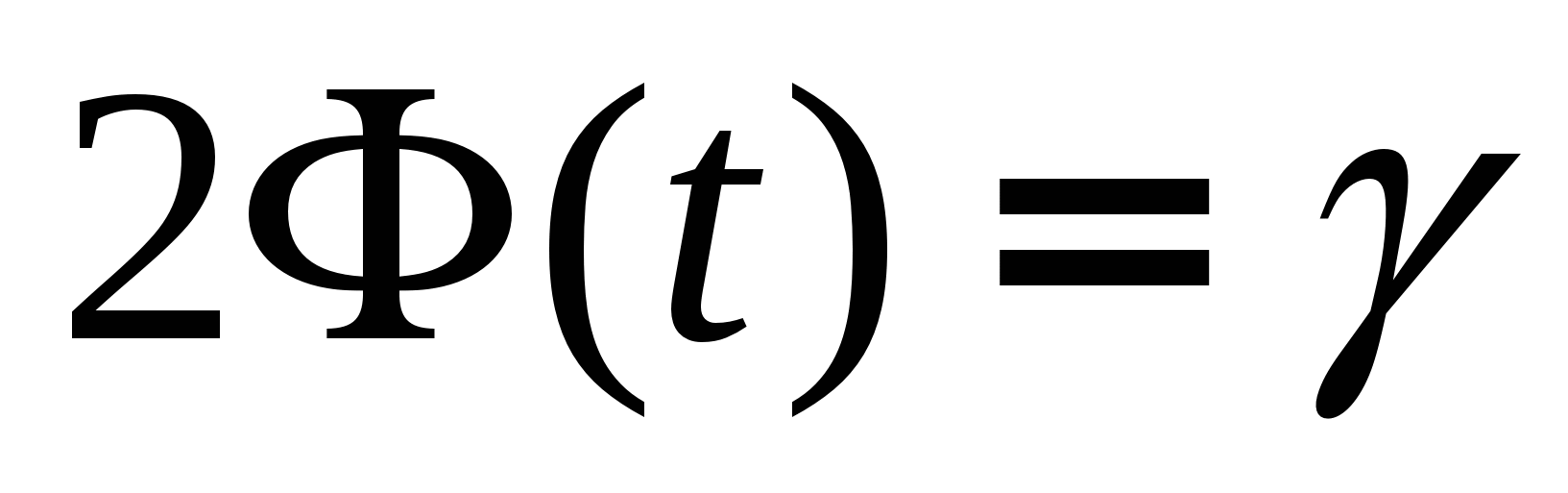 ;
(8)
Таким чином, остаточно отримаємо
;
(8)
Таким чином, остаточно отримаємо
 Тобто
побудований надійний інтервал
Тобто
побудований надійний інтервал
 (9)
заключає
в собі невідомий параметр а
(математичне сподівання) з ймовірністю
.
Число
(9)
заключає
в собі невідомий параметр а
(математичне сподівання) з ймовірністю
.
Число
 при
заданому значенні
знаходимо
із таблиці значень функції Лапласа.
при
заданому значенні
знаходимо
із таблиці значень функції Лапласа.
50 Статистичною гіпотезою називається припущення про вигляд або параметри невідомого закону розподілу, яке може бути перевірене за результатами спостережень.
Висунуту гіпотезу, яку треба перевірити виділяють, як головну і позначають, як правило, H0 (або H), а іншу – як альтернативну (конкуруючу) і позначають H1 (або K). Нульова та конкуруюча гіпотезу являють собою дві можливості вибору, що взаємовиключають одна одну.
Припущення-гіпотези можуть бути різними, та їх можна перевірити за допомогою статистичних даних. Обмеженість вибіркових даних припускає можливість прийняття неправильного рішення. Очевидно, що за статистичними даними важко, а іноді і неможливо робити безпомилкові висновки, при цьому помилки при перевірці гіпотез можуть бути двох родів. Помилка першого роду складається в тому, що відкидається основна гіпотеза, коли вона вірна. При помилці другого роду відкидається вірна конкуруюча гіпотеза. Ймовірність α припуститися помилки першого роду називається рівнем значущості критерію, ймовірність припуститися помилки другого роду зазвичай позначають β. Ймовірність (1–β) не припуститися помилки другого роду називають потужністю критерію.
З
метою перевірки статистичної гіпотези
використовують спеціально складену
випадкову величину (статистику
або критерій)
розподіл якої відомий, її позначають
t,
F
чи Χ2
у залежності від її розподілу (у загальному
вигляді позначимо
![]() ).
Прийняте рішення, щодо нульової гіпотези
опирається на статистичний
критерій – правило
за яким гіпотеза повинна бути прийнята
чи відкинута. Статистичний критерій
розбиває всю множину можливих значень
статистики (критерію)
на
дві множини, що не перетинаються: критичну
область (область відкидання гіпотези)
та область припустимих значень (область
прийняття гіпотези). При перевірці
гіпотези намагаються обрати таку
критичну область, де потужність критерію
буде найбільшою.
).
Прийняте рішення, щодо нульової гіпотези
опирається на статистичний
критерій – правило
за яким гіпотеза повинна бути прийнята
чи відкинута. Статистичний критерій
розбиває всю множину можливих значень
статистики (критерію)
на
дві множини, що не перетинаються: критичну
область (область відкидання гіпотези)
та область припустимих значень (область
прийняття гіпотези). При перевірці
гіпотези намагаються обрати таку
критичну область, де потужність критерію
буде найбільшою.
Вимоги до критичної області аналітично можна записати так:
![]()
![]()
тобто критичну область слід обирати так, щоб ймовірність потрапляння у неї статистики була мінімальною та рівною α, якщо гіпотеза H0 вірна, та максимальною у протилежному випадку. Або іншими словами, критична область повинна бути такою, щоб при даному рівні значущості α, потужність критерію була б найбільшою.
В
залежності від вигляду конкуруючої
гіпотези H1
обирають правосторонню, лівосторонню
або двосторонню критичні області. Так
можна впевнитися, що при конкуруючій
гіпотезі H1:
а>a0
слід використовувати правосторонню
критичну область, у випадку H1:
а<a0
– лівосторонню критичну область, а при
конкуруючій гіпотезі H1:
а≠a0
– двосторонню критичну область. За
таких обставин границі критичних
областей
![]() при
заданому рівні значущості визначаються
з відповідних співвідношень:
при
заданому рівні значущості визначаються
з відповідних співвідношень:
- для правосторонньої критичної області
![]() -
для лівосторонньої критичної області
-
для лівосторонньої критичної області
![]() -
для двосторонньої критичної області
-
для двосторонньої критичної області
![]()
Принцип перевірки статистичної гіпотези не дає логічного доведення її вірності або невірності. Прийняття гіпотези слід розглядати лише як твердження, що не містить протиріч до дослідних даних.
3.
Розглянемо задачу порівняння двох
середніх генеральних сукупностей. Нехай
є дві сукупності, що характеризуються
генеральними середніми
![]() та
відомими
дисперсіями
та
відомими
дисперсіями
![]() та
та
![]() .
Необхідно перевірити гіпотезу про
рівність генеральних середніх H0:
.
Необхідно перевірити гіпотезу про
рівність генеральних середніх H0:
![]()
Для
перевірки гіпотези з цих сукупностей
взято дві незалежні вибірки об’ємами
n1
та n2
за якими знайдено середні арифметичні
![]() та
вибіркові дисперсії
та
вибіркові дисперсії
![]() ,
,
![]() .
.
За достатньо великими об’ємами вибірки вибіркові середні мають спостижено нормальні закони розподілу з параметрами та відповідно.
У
випадку правильної гіпотези H0
різниця
![]() має
нормальний розподіл з математичним
сподіванням
має
нормальний розподіл з математичним
сподіванням
![]() та
дисперсією
та
дисперсією
 (зауважимо,
що дисперсія різниці двох незалежних
величин дорівнює сумі їх дисперсій, а
дисперсія n незалежних доданків в n разів
менша за дисперсію кожного).
(зауважимо,
що дисперсія різниці двох незалежних
величин дорівнює сумі їх дисперсій, а
дисперсія n незалежних доданків в n разів
менша за дисперсію кожного).
Тому при виконання гіпотези H0 статистика
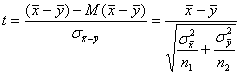
має стандартний нормальний розподіл.
У
випадку конкуруючої гіпотези H1:
![]() (або
H1:
(або
H1:
![]() )
обирають односторонню критичну область
та критичне значення статистики знаходять
з умови
)
обирають односторонню критичну область
та критичне значення статистики знаходять
з умови
![]() (1)а
при конкуруючій гіпотезі H1:
(1)а
при конкуруючій гіпотезі H1:
![]() обирають
двосторонню критичну область, критичне
значення статистики:
обирають
двосторонню критичну область, критичне
значення статистики:
![]() (2)
(2)
Якщо фактичне значення статистики t, що спостерігається більше tкр, що його визначено на рівні значущості α (за абсолютною величиною), тобто |t|>tкр, то гіпотезу H0 відкидаємо, інакше – робимо висновок, що гіпотеза не містить протиріччя до вибіркових даних.
Будемо
вважати, що розподіл ознаки (випадкової
величини) X та Y у кожній сукупності має
нормальний розподіл. В такому випадку,
якщо генеральні дисперсії відомі, то
перевірка гіпотез проводиться таким
самим чином не тільки для великих, але
і для малих за об’ємом вибірок. Якщо ж
дисперсії невідомі проте рівні, тобто
![]() ,
то у якості не відомої величини
,
то у якості не відомої величини
![]() можна
взяти її оцінки – виправлену вибіркову
дисперсію.
можна
взяти її оцінки – виправлену вибіркову
дисперсію.
![]() або
або
![]()
Проте найкращою оцінкою буде дисперсія змішаної сукупності об’єму n1+n2, тобто
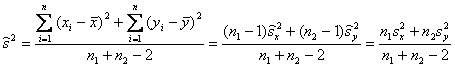
а
оцінкою дисперсії різниці незалежних
вибіркових середніх
![]()
![]()
У випадку справедливості гіпотези H0 статистика
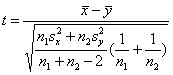
має
t-розподіл Стьюдента з k=n1+n2–2
степенями вільності. Тому критичне
значення статистики t знаходяться за
тими ж формулами (1)-(2), де замість функції
Лапласа береться функція
![]() для
розподілу Стьдента при кількості
ступенів волі k=n1+n2–2,
тобто
для
розподілу Стьдента при кількості
ступенів волі k=n1+n2–2,
тобто
![]() (3)
(3)
![]() (4)
(4)
При цьому правило відкидання (прийняття) гіпотези зберігається.
