43 Марківські випадкові процеси

Багато складних систем, що змінюються в часі, доцільно розглядати як випадкові процеси, хід яких залежать від ряду випадкових чинників, супроводжуючих цей розвиток.

Для того, щоб обчислити числові параметри, характеризуючи такі системи, потрібно побудувати деяку імовірнісну модель явища, що враховує супроводжуючі його випадкові чинники.

Нехай є деяка система S, стан якої міняється з часом (під системою S може розумітися що завгодно: технічний пристрій, виробничий процес, обчислювальна машина, інформаційна мережа і т. д.). Якщо стан системи S міняється в часі випадковим, наперед непередбачуваним чином, говорять, що в системі протікає випадковий процес.

Конкретне протікання кожного з таких процесів залежить від ряду випадкових, наперед непередбачуваних чинників.

Для математичного опису багатьох випадкових процесів може бути застосований апарат, розроблений в теорії ймовірності для так званих марківських випадкових процесів. Випадковий процес, що протікає в системі S, називається марківським (або «процесом без післядії»), якщо він володіє наступною властивістю: для кожного моменту часу t₀ ймовірність будь-якого стану системи в майбутньому (при t> t₀) залежить тільки від її стану в сьогоденні (при t= t₀) і не залежить від того, коли і яким чином система прийшла в цей стан (тобто як розвивався процес у минулому).

Іншими словами, в марківському випадковому процесі майбутній розвиток залежить тільки від його справжнього стану і не залежить від «передісторії» процесу.На практиці часто зустрічаються випадкові процеси, які з тим або іншим ступенем наближення можна вважати марківськими. Теорія марківських випадкових процесів є обширним розділом теорії ймовірності з широким спектром різних додатків - від опису фізичних явищ типу дифузії або перемішування шихти під час плавки в доменній печі до процесів утворення черг або розповсюдження мутацій в біологічній популяції.Марківські випадкові процеси діляться на класи за деякими ознаками, залежно від того, як і в які моменти часу система може міняти свої стани.Випадковий процес називається процесом з дискретними станами, якщо можливі стани системи S₁, S₂, S₃, … можна перерахувати (перенумерувати) одне за іншим, а сам процес полягає в тому, що час від часу система S стрибком (миттєво) переходить з одного стану в інший.Окрім процесів з дискретними станами існують випадкові процеси з безперервними станами: для цих процесів характерний поступовий, плавний перехід із стану в стан. Наприклад, процес зміни напруги в освітлювальній мережі є випадковим процесом з безперервними станами.При аналізі випадкових процесів з дискретними станами зручно користуватися так званим графом станів і переходів (ГСП) (рис. 1). ГСП графічно зображає можливі стани системи і її можливі переходи із стану в стан.

Нехай є система S з n дискретними станами: Кожен стан зображається прямокутником, а можливі переходи («перескоки») із стану в стан - стрілками, що сполучають ці прямокутники.

Відмітимо, що стрілками наголошуються тільки безпосередні переходи із стану в стан; якщо система може перейти з cтану S1 в S3 тільки через S2, тоді стрілками відмічаються тільки переходи S1–S2 і S2–S3, але не S1–S3.

Нехай система S - прилад, який може знаходитися в одному з п'яти можливих станів: S1 - справний, працює; S2- несправний, чекає огляду; S3 - оглядається; S4 - ремонтується; S5- списаний.

Випадкові процеси з дискретним і безперервним часом. Марківські ланцюги

Способи опису марківського випадкового процесу, що протікає в системі з дискретними станами, залежать від того, в які моменти часу - наперед відомі або випадкові - можуть відбуватися переходи («перескоки») системи із стану в стан.

Випадковий процес називається процесом з дискретним часом, якщо переходи системи із стану в стан можливі тільки в строго визначені, наперед фіксовані моменти часу: t₁,t₂,…, і т.д. В проміжки часу між цими моментами система S зберігає свій стан.

Випадковий процес називається процесом з безперервним часом, якщо перехід системи із стану в стан можливий в будь-якій, наперед невідомий, випадковий момент t.

Розглянемо перш за все марківський випадковий процес з дискретними станами і дискретним часом.

Нехай є система S, яка може знаходитися в станах:

S₁, S₂, S₃ ,…, S_n,

причому зміни стану системи можливі тільки в моменти:

t₁, t₂,…, t_k,…Називатимемо ці моменти «кроками» або «етапами» процесу і розглядати випадковий процес, що відбувається в системі S, як функцію цілочисельного аргументу: 1, 2, ..., k, ... (номери кроку). Випадковий процес, що відбувається в системі, полягає в тому, що в послідовні моменти часу t₁, t₂, …, t_k,… система S опиняється в тих або інших станах, поводячись, наприклад, таким чином (у загальному випадку система може не тільки міняти стан, але і зберігати колишнє):

S₁ – S₃ – S₃ – S₃ – S₃ – S₄ – S₄ – S₂ – S₁ – …Умовимося позначати подію, що полягає в тому, що після k кроків система знаходиться в стані S_i . При будь-якому події

утворюють повну групу і несумісні.

Процес, що відбувається в системі, можна представити як послідовність (ланцюжок) подій, наприклад: Така випадкова послідовність подій називається марківським ланцюгом, якщо для кожного кроку ймовірність переходу з будь-якого стану S_i в любе S_j не залежить від того, коли і як система прийшла в стан S_i..

Марківський ланцюг можна описати за допомогою ймовірності станів. Нехай у будь-який момент часу (після будь-якого k-го кроку) система S може бути в одному із станів: S₁, S₂, S₃ ,…, S_n, тобто здійсниться одне з повної групи несумісних подій:

Позначимо ймовірність цих подій для k-го кроку через:

Легко бачити, що для кожного номера кроку до

оскільки це - ймовірність несумісних подій, що створюють повну групу.

Ймовірність називатимемо ймовірністю стану.

У сукупності вони утворюють вектор: (1)

Випадковий процесі (марківський ланцюг) можна уявити собі так, як ніби точка, що зображає систему S, випадковим чином переміщається (блукає) по графу станів, перескакуючи із стану в стан в моменти t₁, t₂,…, t_k,…, а іноді (у загальному випадку) затримуючись на якесь число кроків в одному і тому ж стані.

Для будь-якого кроку (моменту часу t₁, t₂,…, t_k,…або номера 1,2,…,k,…) існує деяка ймовірність переходу системи з будь-якого стану в будь-який інший (деякі з них рівні нулю, якщо безпосередній перехід за один крок неможливий), а також ймовірність затримки системи в даному стані. Називатимемо цю ймовірність перехідною ймовірністю марківського ланцюга.

Марківський ланцюг називається однорідним, якщо перехідна ймовірність не залежить від номера кроку. Інакше марківський ланцюг є неоднорідним.Розглянемо однорідний марківський ланцюг. Позначимо через ймовірність переходу за один крок з стану S_i в стан S_j; P_ii буде ймовірність затримки системи в стані S_i. Запишемо дану ймовірність у формі квадратної матриці:

(2)

Деякі з перехідних ймовірностей P_ij можуть бути рівні нулю, що означає неможливість переходу системи із i-го стану в j-е за один крок. По головній діагоналі матриці перехідної ймовірності стоять ймовірності P_ii того, що система не вийде з стану S_i, залишиться в ньому.

Сума членів, що стоять в кожному рядку матриці (2), повинна бути рівна одиниці, оскільки в якому б стані система не була перед k-м кроком події несумісні і утворюють повну групу.

При розгляді марківських ланцюгів часто буває зручно користуватися ГСП, на якому у стрілок проставлена відповідна перехідна ймовірність (див. рис. 1, б), або розміченим графом станів.

Відмітимо, що на рис. 1, б проставлена не всі перехідні ймовірності, а тільки ті з них, які не рівні нулю і зміняють стан системи, тобто P_ij при “ймовірності затримки” P₁₁, P₂₂ і т.д. проставляти на графі не потрібно, оскільки кожна з них доповнює до одиниці суму перехідної ймовірності, що відповідає всім стрілкам, що витікають з даного стану. Наприклад, для графа рис. 2.1, б:

; ; .

Якщо з стану S_i не виходить жодної стрілки (перехід з нього ні в який інший стан неможливий), відповідна ймовірність затримки P_ii рівна одиниці.

Маючи в розпорядженні розмічений ГСП (або, що рівносильно, матрицю перехідної ймовірності) і знаючи початковий стан системи, можна знайти ймовірність станів після будь-якого (k-го) кроку.

Припустимо, що в початковий момент (перед першим кроком) система знаходиться в якомусь певному стані, наприклад S_m. Тоді для початкового моменту (0) матимемо:

тобто ймовірність всіх станів рівна нулю, крім того ймовірність початкового стану S_m рівна одиниці.

Знайдемо ймовірність станів після першого кроку. Ми знаємо, що перед першим кроком система свідомо знаходиться в стані S_m . Значить, за перший крок вона перейде в стани S₁, S₂, …, S_m ,…, S_n з вірогідністю

,

що знаходяться в m-й рядку матриці перехідної ймовірності. Таким чином, ймовірність станів після першого кроку буде:

. (4)

Знайдемо ймовірність станів після другого кроку:

Обчислюватимемо їх за формулою повної ймовірності з гіпотезами:

- після першого кроку система була в стані S₁; - після першого кроку система була в стані S₂;- після першого кроку система була в стані S_i;- після першого кроку система була в стані S_n

Ймовірності гіпотез відомі (3); умовна ймовірність переходу в стані S_i при кожній гіпотезі теж відомі і записані в матриці перехідної ймовірності. По формулі повної ймовірності одержимо:

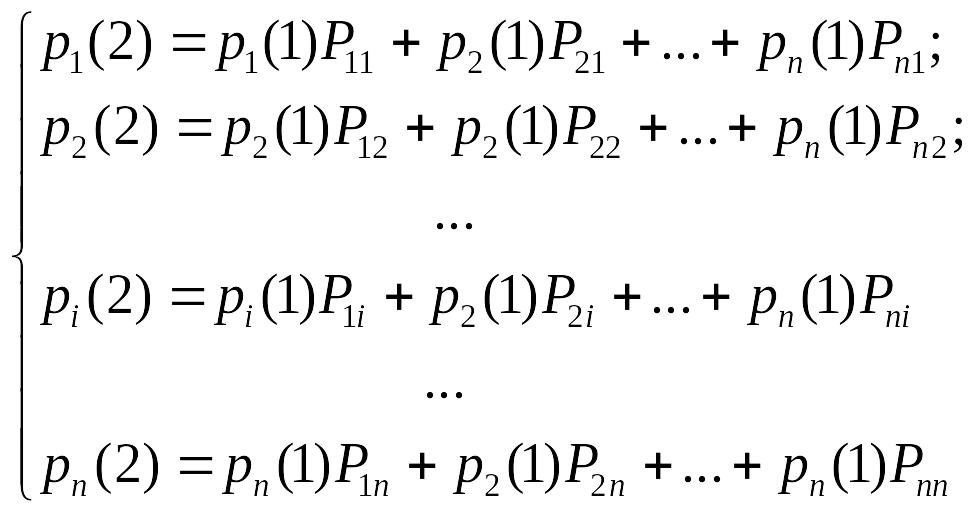(5)

або

, (6)

Даний вираз може бути записаний у вектор-матричній формі:

(7)

де - транспонована матриця (2).

У формулах (6) -(7) підсумовування розповсюджується формально на всі стани S₁, S₂, …, S_m ,…, S_n , але фактично враховувати треба тільки ті з них, для яких перехідні ймовірності P_ji не дорівнюють нуля, тобто ті стани, з яких може здійснитися перехід в стан S_і (або затримка в ньому).

Таким чином, ймовірність станів після другого кроку відома. Очевидно, після третього кроку вони визначаються аналогічно:

і взагалі після k-го кроку: , (8)

або в матричній формі (9)

Отже, ймовірність станів р_і(k) після k-го кроку визначається рекурентною формулою (8) через ймовірність станів після (k - 1) -го кроку; ті, у свою чергу, - через ймовірність станів після (k - 2) -го кроку, і т.д.

Окрім однорідних марківських ланцюгів, в яких ймовірність переходу від кроку до кроку не міняється, відомі динамічні або неоднорідні ланцюги, в яких ймовірність переходу P_ij змінюється від кроку до кроку (залежать від номера кроку k).

В цьому випадку вирази (8), (9) набувають вигляду: ; (10)

44 Пуассо́нівський проце́с — це поняття теорії випадкових процесів, що моделює кількість випадкових подій, що стались, якщо тільки вони відбуваються зі сталим середнім значенням інтервалів між їхніми настаннями. У випадку вибраних одиниць вимірювання, це середнє значення дорівнює кількостей подій за одиницю часу, де λ — параметр процесу. Цей параметр часто називають інтенсивністю пуассонівського процесу.

Якщо розглянути послідовність часових інтервалів між подіями пуассонівського процесу, то ця послідовність буде послідовністю незалежних випадкових величин, яка має назву пуассонівського потоку.

Випадковий процес з неперервним і невід'ємним часом та дискретним станами називається пуасонівським, якщо:

• 1) він є процесом з незалежними приростами;

• 2) для нього виконується однорідність по часу;

• 3) його часовий переріз при t=0 являє собою випадкову величину, тотожньо рівну нулю (ще кажуть: випадковий процес починається в нулі);

• 4) при h прямує до 0 вірними будуть твердження:

• а) ймовірність того, що у момент часу h випадковий процес набуде значення 0, дорівнює 1-λh+o(h);

• б) ймовірність того, що у момент часу h випадковий процес набуде значення 1, дорівнює λh+o(h);

• в) ймовірність того, що у момент часу h випадковий процес набуде значення 2, дорівнює o(h);

де o(h) — величина, порядок малості якої вищий, ніж h; λ — параметр, що визначає процес.

45 Генеральною сукупністю називають об’єкт дослідження, на який розповсюджують висновки соціологічного аналізу. Розрізняють кінцеву і без кінцеву, конкретні і гіпотетичні, однорідні та неоднорідні генеральні сукупності.

Вибіркова сукупність –це певна кількість елементів генеральної сукупності, які відібрані за певним правилом.

Елементи вибіркової сукупності (респонденти, документи, що аналізуються), які підлягають вивченню (опитуванню, інтерв’юванню), називають, одиницями аналізу. Ними можуть бути окремі люди, групи, трудові колективи.Вибірка виступає у двох осн. видах як 1-випадкова 2-стратифікована

При випадковій вибірці з ген. сук-ті одиниці абстрагування вибираються випадковим чином, тобто так, що кожен елемент ген. сук-ті має рівну можливість потрапити у сукупність вибірково. Випадковий відбір йде за будь-яким обраним принципом.

При стратифікованій вибірці відбір здійснюється з урахуванням питомої ваги кожної групи опитуваних в генеральної сукупності.

Розробка методичних інструментів досл. включає обґрунтування відповідних методів збору, обробки і соц. аналізу.

Роб. план досл. – документ, в якому в хронологічній послідовності розписується перелік необхідних робіт за видами і вказується кому, що робити.

Визначення та види вибірки у соціологічних дослідженнях. Щоб підготувати дослідження, необхідно обрати для нього об’єкт. Метод вибірки – це науковий підхід, що дозволяє судити про цілісний об’єкт, ґрунтуючись на даних лише його окремих ознак.

Генеральна сукупність об’єкта – це об’єкт соціального дослідження в цілісності його якостей та ознак.

Вибіркова сукупність – це частина об’єкта генеральної сукупності, що становить суму вихідних одиниць вивчення, спостереження та аналізу.

Репрезентативність – це принцип подоби, вибірково сформульованої моделі параметрів генеральної сукупності. Види вибірки: 1)Проста вибірка включає простий випадковий відбір, систематичний відбір, серійну та гніздову вибірку.2)Складна: багатощаблева, комбіновано, стратифікована, квотна.Одиниця відбору – це районування, що будується за принципом статистичної серії.

Емпірична функція розподілу

Нехай відомо статистичний розподіл частот кількісної ознаки X. Введемо значення п х -- число спостережень, менше х; п -- загальне число спостережень (об'єм вибірки). Ясно, що відносна частота події X <1 дорівнює n(x)/п. Якщо х змінюється, то, взагалі говорячи, змінюється і відносна частота, тобто відносна частота пх /п є функція від х. Тому що ця функція знаходиться емпіричним (досвідченим) шляхом, то її називають емпіричною.

Емпіричною функцією розподілу (функцією розподілу вибірки) називають функцію F*(x), що визначає для кожного значення х відносну частоту випадку X < х. 'Отже, по визначенню:F(x)=nx/n

Де nx-число варіант, менших х; п -- об'єм вибірки. Таким чином, для того щоб знайти, наприклад, F*(xi), потрібно число варіант, менших хг, розділити на об'єм вибірки: F*(x2) = nx2/n.На відміну від емпіричної функції розподілу вибірки функцію розподілу F (х) генеральної сукупності називають теоретичною функцією розподілу. Різниця між емпіричної і теоретичної функціями полягає в тому, що теоретична функція F (х) визначає імовірність події X < х, а емпірична функція F* (х) визначає відносну частоту події. З теореми Бернуллі випливає, що відносна частота події X < х, тобто F* (х) прагне по імовірності до імовірності F (х) цієї події. Іншими словами, при великих п числа F* (х) і F (х) мало відрізняються одне від іншого в тому змісті, що lim n-Р [ | F (х)- F* (х) | < е] = 1 (е > 0). Уже звідси випливає доцільність використання емпіричної функції розподілу вибірки для наближеного представлення теоретичної (інтегральної) функції розподілу генеральної сукупності. Такий висновок підтверджується і тим, що F*(x) наділене усіма властивостями F (х). Дійсно, з визначення функції F* (х) випливають наступні її властивості: 1) значення емпіричної функції належать відрізку [О, 1];

2) F*(x) -- функція, що не спадає;

3) якщо Xi -- найменша варіанта, то F*(x) = Q при xx1; якщо xk--найбільша варіанта, то F* (х) = 1 при x> xk.Отже, емпірична функція розподілу вибірки служить для оцінки теоретичної функції розподілу генеральної сукупності