38. Теорема Чебишова

Теорема Чебишова. Нехай { }- послідовність незалежних випадкових величин, існують D i D при всіх n. Тоді

. (* )

Наслідок. Нехай ₁, ₂ ,…, _n,…- послідовність незалежних випадкових величин така, що М =а, D , n=1,2,…

Тоді для кожного

.

Цей частковий випадок теореми Чебишова дає обгрунтуваня правилу середнього арифметичного в теорії обробки результатів вимірювання. Припустимо, що необхідно виміряти деяку фізичну величину а. Повторюючи вимірювання n раз в одинакових умовах, спостерігач одержує результати вимірювань ₁, ₂ ,…, _n [1]. Якщо спостереження не мають систематичної помилки, тобто М =а, то згідно сформульованому вище наслідку,

 

39. Теорема Бернуллі

Теорема Бернуллі стверджує: якщо т - кількість подій А в п попарно незалежних випробуваннях, а р є ймовірність настання події А в кожнім з випробувань, то при будь-якому є>0 справедлива нерівність

Ця формула є першим в історії варіантом закону великих чисел і по суті вважається початком теорії ймовірностей як галузі математичної науки. Відтоді теорії вибіркового методу стають основою математичної статистики.

Теорема Бернуллі дає можливість оцінити кількості незалежних випробувань п при певних умовах їх проведення.

Приклад 3.16. Ймовірність того, що навмання вибраний студент складе залік, дорівнює 90%. Скільки треба перевірити студентів, щоб з імовірністю 80% виявити успішно підготовлених студентів. Похибка при цьому не повинна перевищувати 10%.

Рішення:

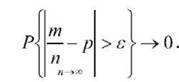
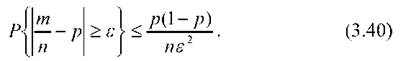
Визначимо відповідні до теореми Бернуллі позначення:

р = 0,90 - ймовірність того, що навмання вибраний студент складе залік;

є = 0,10 - похибка процедури перевірки студентів;

рі OL - p > o_,101 =0,80 - ймовірність виявлення підготовлених студентів.

І^п J

Значення ймовірності не перевищити похибку у 10% процедури перевірки студентів складає

р|^L - p < 0,ю|=1 - 0,80 = 0,20.

При цьому повинна виконуватися нерівність правої частини виразу (3.40)

^p^ < 0,20.

пє

Звідси кількість студентів, яких треба перевірити, визначиться як

p(1 - p) 0,90 o (1 - 0,90) 0,90 o 0,10 0,20 -є¹ 0,20 o (0,10)² 0,20 o 0,01

Відповідь: для того, щоб з імовірністю 80% виявити успішно підготовлених студентів з похибкою не вище 10%, треба перевірити більше ніж 45 осіб.

Одним з принципових питань математичної статистики є характер співвідношення параметра є і кількості незалежних випробуваннях п. Відповідь на це питання також дає закон великих чисел.

40 Центральна гранична теорема — теорема теорії ймовірностей про збіжність розподілу суми незалежних однаково розподілених випадкових величин до нормального розподілу. Ця теорема підкреслює особливість нормального розподілу в теорії ймовірностей.

Центральна гранична теорема для незалежних послідовностей

Формулювання Ліндеберга

Нехай — послідовність взаємно незалежних випадкових величин з однаковими розподілами. Припустімо, що та існують. Нехай . Тоді для довільних фіксованих , ( ):

Де — нормальна функція розподілу

Формулювання Ляпунова

Теорема названа на честь російського математика Олександра Ляпунова. У цьому варіанті центральної граничної теореми випадкові величини мають бути незалежними, але не обов'язково однаково розподіленими. Теорема також вимагає щоб випадкові виличини мали скінченні моменти деякого порядку (2 + δ) і швидкість зростання цих моментів має бути обмежена умовою Ляпунова.

ЦГТ Ляпунова^[3]: Нехай {X_i} — послідовність незалежних випадковех величин, таких, що кожна з них має скінченне математичне сподівання і дисперсію . Позначимо . Якщо для деякого виконується умова Ляпунова

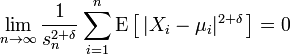
Тоді сума прямує за розподілом до стандартного нормального розподілу, при

На практиці зазвичай найлегше перевірити умову Ляпунова для . Якщо послідовність випадкових величин задовольняє умову Ляпунова, то вона задовольняє також умову Лінденберга. Зворотне твердження не правильне.

Формулювання Лінденберга

Використовуючи ті позначення що й у попередньому параграфі, замінюючи умову Ляпунова на слабшу (запропоновану фінським математиком Ліндебергом у 1920 році) можна отримати нове формулювання центральної граничної теореми.

Якщо для кожного виконуэться

де — характеристична функція. Тоді розподіл стандартизованої суми Z_n прямує до стандартного нормального розподілу N(0,1).

41 Випадковим процесом називається процес, значення якого за будь-якого значення аргументу t є випадковою величиною.

Реалізацією випадкового процесу називається детермінована функція , на яку перетворюється випадковий процес внаслідок випробування, тобто його траєкторія.

Кілька реалізацій певного випадкового процесу зображено на рис. 4.1. Нехай переріз цього процесу при даному t є неперервною випадковою величиною. Тоді випадковий процес при даному t визначається щільністю ймовірності

Очевидно, що щільність імовірності не є вичерпним заданням випадкового процесу , оскільки вона не виражає залежності між його перерізами в різні моменти часу.

Випадковий процес являє собою сукупність усіх перерізів за всіх можливих значень t, тому для його задання необхідно розглядати багатовимірну випадкову величину утворену з усіх перерізів цього процесу.

Таких перерізів нескінченно багато, але для задання випадкового процесу вдається обмежитись порівняльно невеликою кількістю перерізів.

Рис. 11.1

Випадковий процес має порядок п, якщо він повністю визначається щільністю спільного розподілу п довільних перерізів процесу, тобто щільністю п-вимірної випадкової величини де — переріз випадкового процесу у момент часу

Випадковий процес може бути заданий числовими характеристиками.

Математичним сподіванням випадкового процесу називається детермінована функція яка за будь-якого значення змінної t дорівнює математичному сподіванню відповідного перерізу випадкового процесу , тобто

Дисперсією випадкового процесу називається детермінована функція , яка за будь-якого значення змінної t дорівнює дисперсії відповідного перерізу випадкового процесу , тобто

Середнім квадратичним відхиленням випадкового процесу називається арифметичне значення квадратного кореня з його дисперсії, тобто

Математичне сподівання випадкового процесу характеризує середню траєкторію всіх можливих його реалізацій, а його дисперсія або середнє квадратичне відхилення — розкид реалізацій відносно середньої траєкторії.

Кореляційною функцією випадкового процесу називається детермінована функція:

двох змінних і , яка для кожної пари змінних і дорівнює коваріації відповідних перерізів і випадкового процесу.

Кореляційна функція характеризує не лише ступінь близькості лінійної залежності між двома перерізами, а й розкид цих перерізів відносно математичного сподівання

Тому розглядається також нормована кореляційна функція випадкового процесу.

Нормованою кореляційною функцією випадкового процесу називається функція

42Ланцюг Маркова в математиці це випадковий процес, що задовольняє властивість Маркова і який приймає скінченну чи зліченну кількість значень (станів). Існують ланцюги Маркова як з дискретним так і з неперервним часом. В даній статті розглядається дискретний випадок.

Інтуїтивне визначення Нехай I -деяка скінченна чи зліченна множина елементи якої називаються станами. Нехай деякий процес в момент часу n (де n=0,1,2,3…) може перебувати в одному із цих станів, а в час n+1 перейти в деякий інший стан(чи залишитися в тому ж). Кожен такий перехід називається кроком. Кожен крок не є точно визначеним. З певними ймовірностями процес може перейти в один з кількох чи навіть усіх станів. Якщо імовірності переходу залежать лише від часу n і стану в якому перебуває процес в цей час і не залежать від станів в яких процес перебував у моменти 0, 1, … , n-1 то такий процес називається (дискретним) ланцюгом Маркова. Ланцюг Маркова повністю задається визначенням ймовірностей p_i перебування процесу в стані в час n=0 і ймовірностей переходу зі стану в стан в час n. Якщо ймовірності переходу не залежать від часу (тобто однакові для всіх n) то такий ланцюг Маркова називається однорідним. Саме однорідні ланцюги Маркова є найважливішими на практиці і найкраще вивченими теоретично. Тому саме їм приділятиметься найбільша увага у цій статті.

Формальне визначення

Послідовність дискретних випадкових величин називається ланцюгом Маркова (з дискретним часом), якщо

.

Тобто майбутні значення послідовності залежать лише від теперішнього стану і не залежать від минулих.

Матриця , де

називається ма́трицею ймовірностей переходу на -му кроці, а вектор , де

— початковим розподілом ланцюга Маркова.

Очевидно, матриця ймовірностей переходу є стохастичною, тобто

.

Ланцюг Маркова називається однорідним якщо:

,

або еквівалентно:

для всіх n.