35. Геометричний розподіл та його числові характеристики

Геометрическое распределение. Дискретная случайная величина Х имеет геометрическое распределение, если ее возможные значения 0, 1, 2, ... , m, … , а вероятности этих значений:

          (25)

где 0 < p < 1,  q = 1 – p ;  m = 0, 1, 2, ... .

Вероятности Рm для последовательных значений m образуют геометрическую прогрессию с первым членом р и знаменателем q, откуда и название «геометрическое распределение».

В качестве примера рассмотрим стрельбу по некоторой цели до первого попадания, причем вероятность попадания при каждом выстреле не зависит от результатов предыдущих выстрелов  и сохраняет постоянное значение р (0 < p < 1). Тогда количество произведенных выстрелов будет случайной величиной с геометрическим распределением вероятностей. 

Геометрическое распределение определяется одним параметром р. Cлучайная величина, подчиненная геометрическому закону распределения, имеет следующие основные числовые характеристики:

36. Початкові та центральні моменти. Асиметрія та ексцес

Приведем краткий обзор характеристик, которые применяются для анализа вариационного ряда и являются аналогами соответствующих числовых характеристик случайной величины.      Начальным выборочным моментом k-го порядка называется величина, определяемая по формуле:       ,      где х_i – наблюдаемое значение с частотой n_i, n – число наблюдений. В частности, начальный выборочный момент первого порядка обозначается   и называется выборочной средней:       .      Медианой называется значение признака, приходящееся на середину ранжированного ряда наблюдений.      Модой называется вариант, которому соответствует наибольшая частота.      Вариационный размах R равен разности между наибольшим и наименьшим вариантом ряда.      Центральным выборочным моментом k-го порядка называется величина, определяемая по формуле:       .      В частности, центральной выборочный момент второго порядка обозначается S² и называется выборочной дисперсией:       .      Средним квадратическим отклонением S называется арифметическое значение корня квадратного из дисперсии: 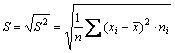      .      Коэффициентом вариации называется отношение среднего квадратического отклонения к средней, выраженное в процентах:       .      Справедливы следующие формулы, выражающие центральные выборочные моменты различных порядков через начальные:              и т.д.      Выборочным коэффициентом асимметрии называется число , определяемое формулой       .      Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона (см. далее) вариационного ряда. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая.      В случае отрицательного коэффициента асимметрии более пологий «спуск» полигона наблюдается слева, в противном случае – справа. В первом случае асимметрию называют левосторонней, а во втором – правосторонней.      Выборочным эксцессом или коэффициентом крутизны называется число E^˜k, определяемое формулой       .      Выборочный эксцесс служит для сравнения на «крутость» выборочного распределения с нормальным распределением. Ранее подчеркивалось, что эксцесс для случайной величины, распределенной нормально, равен нулю. Поэтому за стандартное значение выборочного эксцесса принимают E^˜k = 0. Если выборочному распределению соответствует отрицательный эксцесс, то соответствующий полигон имеет более пологую вершину по сравнению с нормальной кривой. В случае положительного эксцесса полигон более крутой по сравнению с нормальной кривой.