1. Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка).

Правило суммы: если элемент   можно выбрать   различными способами и независимо от него элемент   можно выбрать   различными способами, то выбрать все различные комбинации элементов «  или  » можно сделать   способами.

Правило произведения: если элемент   можно выбрать   различными способами и независимо от него элемент   можно выбрать   различными способами, то все различные комбинации элементов «  и  » можно выбрать   способами.

Правила суммы и произведения естественным образом обобщаются и на случай комбинаций многих элементов, а именно, если первый элемент совокупности из   различных элементов можно выбрать   способами, второй —   способами и так далее,  -й элемент —  способами, то всевозможных комбинаций соответственно   и  . 

Перестановки без повторений Перестановки в ряд

Перестановкой из   элементов (или  -перестановкой) называется  -элементное упорядоченное множество, составленное из элементов  -элементного множества.

Иначе: Перестановкой из   элементов (или  -перестановкой) называется размещение из  элементов по   без повторений.

Число перестановок из   элементов без повторений обозначается   от французского словаperturbation.

Теорема: число способов расположить в ряд   различных объектов есть

Замечание: Рекуррентная формула:  .

Перестановки симметричных объектов

 различных предметов можно расположить по кругу   способами, а если их можно еще и переворачивать, то   различными способами.

Перестановки с повторениями

Пусть даны   элементов первого типа,   — второго типа, ...,   —  -го типа, всего  элементов. Способы разместить их по   различным местам называются перестановками с повторениями. Их количество обозначается  .

Теорема: число перестановок с повторениями есть

2. Размещения без повторений

Подсчитаем количество способов расположить   различных элементов по   различным позициям ( ). Такие расположения называются размещениями, а их количество, от французского слова arrangement обозначается  . В случае, если   количество предметов совпадает с количеством имеющихся мест, и это уже изученная задача о числе перестановок.

Если из   объектов выбирают   штук, то число выборов последнего объекта есть  невыбранных объектов, что означает наличие   возможности выбора последнего выбранного объекта. То же, другими словами: после выбора первых   элемента остается выбрать   элемент.

Теорема: число размещений   различных элементов по   различным позициям есть

,

или, в терминах факториалов,

.

Примечание: заметим, что в случае, когда число мест, по которым размещают предметы, совпадает с количеством самих предметов, т. е. когда  , рассматриваемая задача становится задачей о числе перестановок. В нашем случае при этом мы получаем в знаменателе дроби ноль факториал, и для того, что бы разные формулы, соответствующие одной и той же задаче, приводили к одинаковым результатам, полагают, что  .

Размещения с повторениями

Пусть даны   различных видов предметов, которые можно разместить по   различным местам, причем выбирать предметы можно с повторениями (т.е. можно выбрать несколько предметов одного вида). Такие выборки называются размещениями с повторениями, а их количество вычисляется по формуле:  .

3. Комбiнацiї без повторень — це сполуки, якi мають такi характернi ознаки:

1. Елементи у сполуцi не повторюються.

2. Кiлькiсть мiсць (m) у сполуцi не бiльша нiж кiлькiсть елементiв (n), якi претендують на цi мiсця (m ≤ n).

3. Порядок розташування елементiв у сполуцi не має значення.

Кiлькiсть комбiнацiй обчислюють за формулою 

C_n^m = n! / (m!·(n — m)!)

5.Треугольник Паскаля

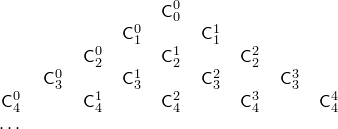В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа  .

Теорема. 

Доказательство. Рассмотрим множество из   элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из   элементов данного множества, в каждой из которых никакой элемент не встречается дважды?

1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член

2 способ. Выберем сначала   элементов из данного множества, а затем расположим их в некотором порядке

Домножим числитель и знаменатель этой дроби на  :

Бином Ньютона

Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона:

(a + b)ⁿ = aⁿ + C¹_n a^{n - 1} b + C²_n a^{n - 2} b² +...+C^k_n a^{n - k} b^k +... + C^{n - 1}_n ab^{n - 1} + Cⁿ_nbⁿ

или (после подстановки выражений C^k_n с учетом формулы C^k_n = C^{n - k}_n):

где C^k_n — число всех возможных сочетаний, которые можно образовать из n элементов по k.

Пример: (a + b)⁵ = a⁵ + C¹₅ a⁴b + C²₅ a³b² + C³₅ a²b³ + C⁴₅ ab⁴ + C⁵₅ b⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵