2.4 Розрахунок зубчастої передачі редуктора
2.4.1 Вибираємо матеріали з табл.3.3/1/с.34; для шестерні - Сталь 45, термічна обробка поліпшення, твердість НВ 269; для колеса Сталь 45, термічна обробка - поліпшена, твердість НВ 302.
2.4.2 Допустимі контактні напруження:
,
(2.25)
де σHlimb – межа витривалості робочих поверхонь зубців./1/, табл.3.2. Приймаємо σHlimb=2НВ+70;
КHL=1- коефіцієнт довговічності, /1/, с.33;
[SH]=1,1 - коефіцієнту безпечності, /1/, с.33.
2.4.3 Визначаємо для прямозубих коліс розрахункове контактне допустиме напруження, МПа:
для шестерні
(2.27)
для колеса
,
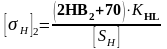(2.28)
Тоді допустиме контактне напруження [σH]=[σH2]=518 МПа.
2.4.4 Міжосьова відстань з умови контактної витривалості актив них поверхонь зубів :
,
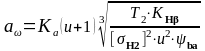(2.29)
де Ка =49,5- для прямозубих коліс;
и=иред=__ - передатне число редуктора;
Т2 =___·103 Н·м – обертовий момент на веденому валу, п.п.2.2, табл.2.1;
КНβ=1 – коефіцієнт , що враховує неравномірність розподілення навантаження по ширині венця. /1/, табл.3.1, с.32;
ψba =0,25 - коефіцієнт ширини вінця по міжосьовій відстані для прямозубих коліс, /1/ с.36.
аω=
Найближче значення міжосьової відстані по ГОСТ 2185 аω=___ мм.
2.4.5 Модуль зачеплення приймаємо по наступній рекомендації:
,
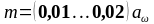(2.30)
m=
Приймаємо по ГОСТ 9563 /1/ с.36 m=__мм.
Далі наведено формули для розрахунку прямозубої передачі
2.4.6 Визначаємо число зубів шестерні і колеса:
,
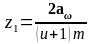(2.31)
Приймаємо z1=___, тоді
,
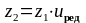(2.32)
z2 =
2.4.7 Основні розміри шестерні та колеса.
Діаметри ділильні,мм:
d1=z1∙m, (2.33)
d1=_____мм
d2=z2∙m , (2.34)
d2=____мм
- для косозубих коліс
2.4.6 Примемо попередньо кут нахилу зубців β= 10º і визначемо кількість зубів
,
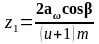(2.31)
z1=
Приймаємо z1=__
, (2.32)
z2 =
Уточнюємо значення кута нахилу зубців:
,
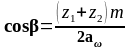(2.33 )
cosβ =
β=__
2.4.7 Основні розміри шестерні і колеса:
- ділильні діаметри
,
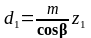(2.34 )
d1=
,
(2.35)
d2=
Далі однаково для прямозубих та косозубих
2.4.8 Перевірка:
,
(2.35)
aw=
2.4.9 Діаметри вершин зубців, мм:
dа1= d1+2m , (2.36)
dа1=
dа2= d2+2m , (2.37)
dа2=
2.4.10 Ширина колеса,мм:
,
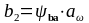(2.38)
b2=
2.4.11 Ширина шестерні,мм:
,
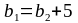(2.39)
b1=
2.4.12 Коефіцієнт ширини шестерні по діаметру:
,
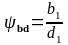(2.40)
ψbd =
2.4.13 Окружна швидкість та ступінь точності передачі,м/с:
,
(2.41)
м/с.
При такій швидкості для прямозубих коліс слід приймати по 8-му ступеню точності по ГОСТ 1643 або /1/ с.32..
2.4.14 Коефіцієнт навантаження:
КH=KHα ·КHβ ·КHv , (2.42)
де KHα=__ – коефіцієнт, що враховує нерівромрність розподілення навантаження між зубцями, /1/ , табл.3.4, с.32;
КHβ =__- коефіцієнт, що враховує нерівромрність розподілення навантаження по ширині вінця, /1/ табл.3.1, с.3;
КHv=__ - динамічний коефіцієнт, що залежить від колової швидкості ν1 та ступені точності їх виготовлення, /1/ табл.3.6, с.32.
КН=
2.4.15 Перевіряємо контактне напруження, МПа:
прямозубих передач
,
(2.43)
косозубих і шевроних передач
,
2.4.16 Сили, діючі в зачепленні, Н:
прямозуба – колова і радіальна
Колова
,
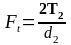(2.44)
Радіальна
Fr=Ft·tgα , (2.45)
косозуба и шевронна – колова,радіальна, осьова
Колова
, (2.44)
Радіальна
Fr=Ft·
, (2.45)
Осьова
Fa = Ft tgβ, (2. )
де α – кут зачеплення;
β – кут нахилу зубів.
2.4.17 Перевіряємо зубці на витривалість по напруженням вигину:
для прямозубих
,
для косозубих
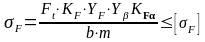(2.47)
де Ft – колова сила,Н;
КF – коефіцієнт навантаження, що визначається за формулою (2.48);
YF – коефіцієнт, що враховує форму зуба, залежить від еквівалентного числа зубів, /1/ с.42;
Yβ – коефіцієнт, що враховує підвищення міцності косих зубців у порівнянні з прямими та визначається за формулою (2.51);
KFα – коефіцієнт,що враховує розподілення навантаження між зубами. Визначається за формулою (2.52);
b2 – ширина зубчастого колеса,мм;
m – нормальний модуль зачеплення, мм.
2.4.18 Визначаємо коефіцієнт навантаження:
KF=KFβ · KFv , (2.48)
де КFβ =___ - коефіцієнт, що враховує нерівромрність розподілення навантаження по довжені зуба, /1/ табл.3.7, с.43;
KFv=___ - коефіцієнт, що враховує динамічну дію навантаження /1/ табл.3.8, с.43
KF=
2.4.19 Визначаємо коефіцієнт YF , залежить від еквівалентного числа зубів zν1 і zν2 , /1/ с.42:
-
для шестерні
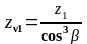, (2.49)
zν1=
для колеса
,
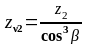(2.50)
zν2 =
При визначених еквивалентних числах зубців zν1=___YF1=____;
zν2 =__YF2=____.
2.4.20 Визначаємо коефіцієнти Yβ :
,
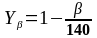(2.51)
де β = ___º - кутнахилу делильної лінії зуба, формула (2.33).
2.4.21 Визначаємо коефіцієнти KFα :
,
(2.52)
де εα = 1,5 – коефіцієнт торцевого перекриття;
n – ступінь точності зубчастих коліс. Була прийнята 8-я ступінь точності.
KFα=
2.4.22 Допустиме напруження визначаємо по формулі:
,
(2.53)
де
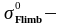межа
витривалості , по /1/, табл.3.9, с.45, для
матеріалу Сталь 45 покращеної, при
твердості НВ≤280 встановлено:
,
(2.54)
для шестерні
для колеса
[SF] – коефіцієнт безпеки.
,
(2.55)
По
табл.3.9/1/с.45
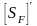=1,75
;
=1
.
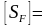
Допустимі напруження:
- для шестерні
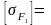
- для колеса
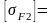
2.4.23
Значення відношення
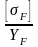, МПа:
для шестерні
для колеса
Подальший розрахунок слід вести для зубів колеса, для якого знайдене відношення менше.
2.4.24 Перевіряємо зуби колеса на витривалість по напруженням вигин
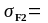
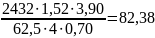
Умова міцності виконана.