4.9. Методы моделирования случайных процессов с заданными характеристиками

Применение рассмотренных выше методов математического моделирования случайных процессов в системах управления связано с рядом ограничений. Построение аналитических моделей возможно только в простейших случаях, а наиболее универсальный из рассмотренных метод динамики средних требует численного интегрирования. Порядок модели, построенной по методу динамики средних, в несколько раз превышает порядок моделируемой системы, а входные воздействия могут учитываться только в форме белых шумов. Поэтому для достаточно сложных задач неизбежно использование статистического имитационного моделирования, несмотря на высокую его трудоемкость. Кроме того, статистическое имитационное моделирование применяется для проверки точности и достоверности результатов, полученных другими методами, требующими более жестких допущений о характеристиках моделируемых процессов.

При статистическом имитационном моделировании на основе математических, полунатурных и других моделей возникает задача имитации внешних воздействий на систему, имеющих форму случайных процессов с определенными характеристиками. Эта задача решается путем построения генераторов случайных процессов.

Рассмотрим задачу имитации одномерного случайного процесса X(t). Получаемые реализации должны подчиняться закону распределения с заданной ПРВ f(x) и иметь заданную корреляционную функцию K_x(). Генератор случайного процесса с заданными характеристиками обычно строится на основе генератора белого шума.

При математическом моделировании используются стандартные генераторы псевдослучайных чисел с равномерным или нормальным законом распределения. Такие генераторы обычно обеспечивают получение последовательностей чисел с достаточно низкой взаимной зависимостью. Если рассматривать такую последовательность ₁,₂,…,_i,…,_n как последовательность значений процесса (t), зарегистрированных в моменты времени t₁<t₂<<t_i<<t_n с постоянным шагом t: (t₁)=₁, (t₂)=₂,  (t_i)=_i, (t_n)=_n, t_i+1=t_i+t, будет получена модель дискретного белого шума. При t0 перейдем к модели непрерывного белого шума. При использовании ЦВМ шаг t всегда конечен. Поэтому его величину приходится учитывать при расчете параметров цифровых моделей непрерывных случайных процессов.

Для получения случайного процесса с названными выше характеристиками из белого шума с равномерным или нормальным законом распределения необходимо обеспечить: заданный закон распределения - эта задача решается рассмотренными выше методами безынерционных нелинейных преобразований; заданные корреляционные свойства - эта задача решается методами формирующего фильтра, скользящего суммирования и др.

4.9.1. Метод формирующего фильтра

Метод формирующего фильтра основан на использовании закономерностей преобразования линейным динамическим звеном спектральной плотности случайного сигнала, описываемых соотношением (4.15). Если на вход динамического звена поступает белый шум со спектральной плотностью S_()=S₀, спектральная плотность выходного сигнала X(t) будет определяться через частотную передаточную функцию звена W(j) следующим образом:

S_x()=|W(j)|²S₀.

Формирующим фильтром называется динамическое звено, обеспечивающее требуемые корреляционные свойства выходного сигнала.

Модель случайного процесса с заданной корреляционной функцией K_x() можно построить на основе формирующего фильтра, используя в качестве его входного сигнала белый шум. Необходимая передаточная функция формирующего фильтра определяется из соотношения

, (4.46)

где

.

Пример. Задана корреляционная функция моделируемого процесса

K_x()=D_xe^{-| |}.

Определим его спектральную плотность:

Пусть имеется генератор белого шума (t) с постоянной интенсивностью, или дисперсией, G₀. Определим его спектральную плотность:

K_()=G₀(), .

Теперь найдем передаточную функцию формирующего фильтра:

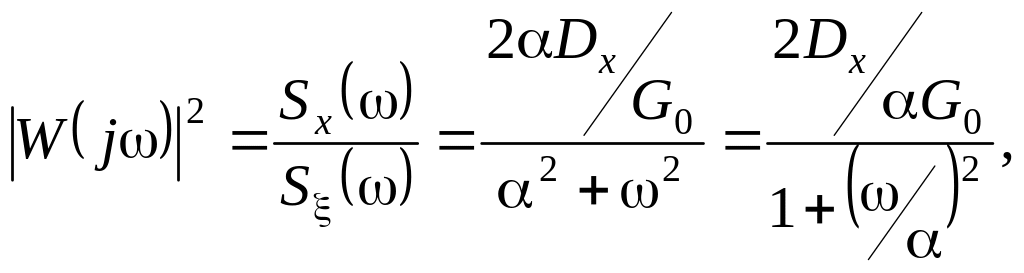
откуда или , где , .

Такой формирующий фильтр может быть физически реализован, например, в виде четырехполюсника (рис. 44, а) или на операционном усилителе (рис. 44, б). Для четырехполюсника k_ф=1, T_ф=RC; для операционного усилителя k_ф=R₂/R₁, T_ф=R₂C. В математической модели, построенной на основе D-схемы, такой формирующий фильтр может быть представлен дифференциальным уравнением:

.

При реализации на ЦВМ математической модели непрерывной системы в форме (4.27) или (4.35) и использовании методов пошагового интегрирования дифференциальных уравнений фактически применяется аппроксимация непрерывного случайного процесса дискретным. Такой дискретный процесс имеет период дискретизации, равный шагу интегрирования h, и сохраняет свое значение в течение периода. Определим корреляционную функцию и спектральную плотность дискретного случайного процесса, аппроксимирующего непрерывный белый шум с интенсивностью G₀:

K_^*()=G₀1()-G₀1(-h),

.

Поэтому, если в качестве источника белого шума используется генератор случайных чисел с некоторым законом распределения, характеризуемым дисперсией D_, в соотношении (4.46) в качестве спектральной плотности входного сигнала для формирующего фильтра следует брать значение S₀=D_h. Например, при использовании стандартного генератора псевдослучайных чисел с равномерным законом распределения в интервале [0; 1] следует брать S₀=h/12.

Отметим, что область использования формирующих фильтров не ограничивается статистическим имитационным моделированием. Так полученные выше основные соотношения метода динамики средних могут использоваться только в предположении, что входные сигналы системы являются белыми шумами. Если необходимо учесть входной сигнал в виде случайного процесса с заданной корреляционной функцией, следует добавить в исходную систему уравнений (4.27) или (4.35) соответствующее уравнение формирующего фильтра.