4.3. Статистическая линеаризация нелинейной стационарной системы

Если моделируемая система включает в себя хотя бы одно нелинейное звено, задача анализа протекающих в ней процессов существенно усложняется. Для нелинейных систем не выполняется принцип суперпозиции. Нелинейное звено вносит существенные искажения в закон распределения преобразуемого сигнала. Тем не менее возможность использования достаточно простых методов анализа случайных процессов, разработанных для линейных систем, удается здесь обеспечить на основе статистической линеаризации системы.

Статистической линеаризацией называется построение линейной модели нелинейного звена системы управления с учетом характеристик преобразования случайного сигнала линейной частью системы.

М

етоды статистической линеаризации основаны на допущении о наличии у линейной части системы свойства фильтра. Благодаря этому, сигнал на входе нелинейного звена, то есть на выходе линейной части (рис. 38), рассматривается в форме , причем для описания центрированной составляющей ограничиваются дисперсией D_x или среднеквадратическим отклонением σ_x. При нескольких входных сигналах для каждого используется аналогичное представление, а для описания совокупности центрированных составляющих - матрица моментов (4.12).

С

татистическая линеаризация проводится для стационарных процессов или для фиксированных значений m_x и σ_x нестационарного случайного процесса, соответствующих некоторому рассматриваемому моменту времени.

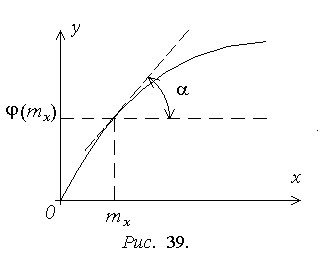
Если статическая характеристика нелинейного звена (x) однозначна и дифференцируема по крайней мере для отрезка [m_x-3σ_x; m_x+3σ_x] и _x достаточно мала, выполняется прямая линеаризация нелинейности в окрестности m_x (рис. 39). В этом случае сигнал на выходе нелинейного звена рассматривается в форме:

, , (4.18)

где (m_x) и '(m_x) - коэффициенты линеаризованной модели нелинейного звена, нелинейно зависящие от m_x;  - угол наклона касательной к функции (x) в точке m_x. Получаемая приближенная зависимость (4.18) оказывается линейной относительно центрированной составляющей входного сигнала , что равноценно замене исходной нелинейной статической характеристики звена касательной в точке, соответствующей m_x.

Для нелинейного звена с несколькими входами статическая характеристика приводится к виду (x₁,x₂,…,x_n). При выполнении для всех входных сигналов x_i указанных выше условий прямая линеаризация осуществляется в следующей форме:

,

, i=1,2,...,n,

где условие x=m_x выполняется для всех аргументов функции .

Таким образом, принцип линеаризации стохастических нелинейных систем аналогичен принципу линеаризации детерминированных систем. Но здесь линеаризация производится не в окрестности состояния равновесия, а в окрестности средних значений (математических ожиданий) входных сигналов.

Если нелинейность является неоднозначной или имеет разрывы 1-го или 2-го рода в пределах отрезка [m_x-3σ_x; m_x+3σ_x], применяется статистическая линеаризация, состоящая в приближенной замене нелинейной характеристики звена эквивалентной в вероятностном смысле линеаризованной зависимостью между входными и выходной переменными.

Рассмотрим сначала звено с одним входом и статической характеристикой (x). В зависимости от вида статической характеристики возможны различные варианты получаемой линеаризованной зависимости.

Для однозначной нелинейности общего вида: .

Для однозначной нечетной относительно входного сигнала нелинейности (-x)=-(x) коэффициент ₀ выражают через математическое ожидание входного сигнала: ₀ = k₀m_x.

Для неоднозначной нелинейности линеаризованную зависимость получают в форме: , где X₁=X, .

Коэффициент ₀ называется средней статистической характеристикой нелинейности; коэффициент k₀ - статистическим коэффициентом усиления по математическому ожиданию; коэффициенты k₁ и k₂ - статистическими коэффициентами усиления по случайным составляющим входных сигналов.

Значения коэффициентов статистической линеаризации определяют на основе критериев вероятностной эквивалентности. Обычно используют два критерия.

Первый критерий состоит в равенстве математических ожиданий и дисперсий сигналов на выходе статистически линеаризованного и исходного нелинейного звеньев. Для однозначной исходной нелинейности имеем:

,

,

где f(x) - ПРВ сигнала X на входе нелинейного звена.

Математическое ожидание выходного сигнала линеаризованного звена M[Y] равно ₀ (или k₀m_x для нечетной нелинейности), а его дисперсия D[Y] связана с дисперсией и среднеквадратическим отклонением входного сигнала в соответствии с (4.15):

В результате получим:

или , (4.19)

. (4.20)

Знак в формуле (4.20) соответствует знаку производной в точке, соответствующей m_x.

Второй критерий состоит в минимизации среднего квадрата ошибки аппроксимации выходного сигнала нелинейного звена выходным сигналом линеаризованного звена:

.

Раскроем скобки в выражении для ² и применим к нему первое необходимое условие экстремума по ₀ и k₁:

,

,

.

Решение полученных уравнений дает выражения для определения ₀ и k₁, доставляющих минимум ²:

,

. (4.21)

Отметим, что для ₀ (и соответственно k₀) оба критерия дают одинаковую расчетную формулу (4.19). Для k₁ получены различные расчетные формулы. Поскольку оба критерия считаются равноценными, обычно рекомендуют вычислять k₁ как среднее арифметическое:

,

где - значение, получаемое на основе первого критерия по (4.20); - значение, получаемое на основе второго критерия по (4.21).

Для нелинейного звена с несколькими входами линеаризация производится в форме:

.

Здесь обычно ограничиваются использованием критерия минимума среднего квадрата ошибки, дающего наиболее простые расчетные соотношения:

.

Повторим выполненную ранее процедуру:

,

,

, i=1,2,...,n, (4.22)

где - корреляционные моменты связи входных сигналов.

В результате средняя статистическая характеристика нелинейности определяется как математическое ожидание сигнала на выходе звена:

₀ = m_y =M[(x₁,x₂,…,x_n)],

а коэффициенты усиления по случайным составляющим входных сигналов k_i - из системы уравнений (4.22).

В частном случае при взаимно независимых входных сигналах звена (_ij = 0 при i≠j) из (4.22) получаем:

, i=1,2,...,n,

где D_xi = _ii.

Все полученные расчетные соотношения для определения коэффициентов статистической линеаризации предусматривают использование ПРВ сигналов на входе линеаризуемого звена. В силу допущения о наличии у линейной части системы свойства фильтра, обычно используется ПРВ нормального закона распределения. Рассмотрим некоторые примеры.

П

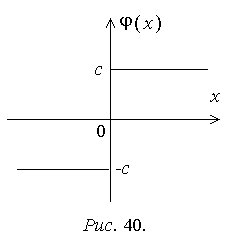
ример 1. Нелинейное звено (рис. 40) с идеальной релейной характеристикой (x)=csignx. Линеаризация выполняется в форме . Для определения k₀ применим формулу (4.19):

,

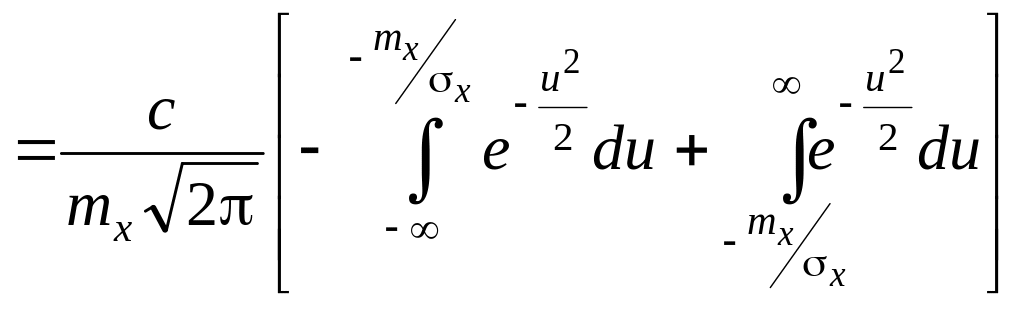где - стандартизованная нормальная величина. И далее:

,

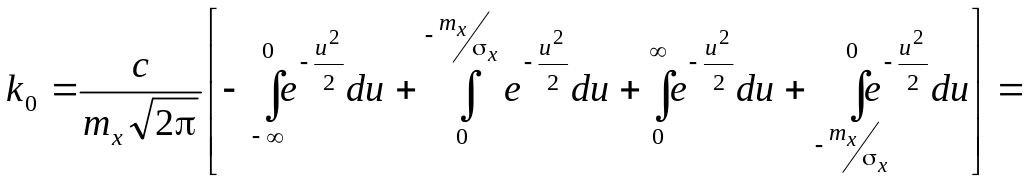
где Ф(u) - интеграл вероятностей, рассмотренный в разд. 3.

Аналогично на основе (4.20), (4.21) можно получить:

,

.

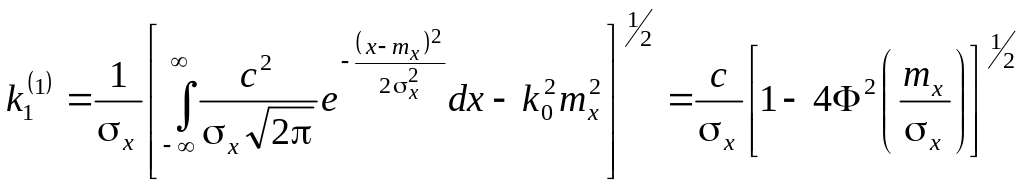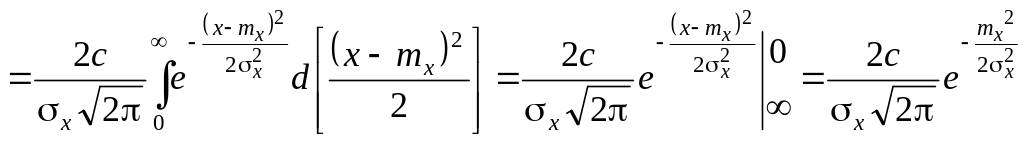Пример 2. Нелинейное звено имеет релейную характеристику с гистерезисом (рис. 41). Неоднозначную зависимость можно формально заменить однозначной:

е

сли рассматривать два входных сигнала: X₁=X и и использовать форму .

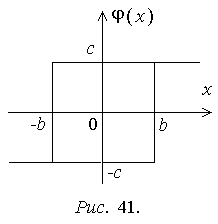
Формулы для расчета коэффициентов статистической линеаризации типовых нелинейных звеньев приводятся в справочных разделах [2, 32, 33].

Отметим в итоге, что коэффициенты статистической линеаризации оказываются функциями статистических характеристик входных сигналов нелинейного звена. Для звена с одним входом ₀, k₀ и k₁ зависят от m_x и σ_x. Для звена с несколькими входами ₀ и n коэффициентов k_i зависят от вектора математических ожиданий входных сигналов и матрицы моментов (4.12).