3.8. Пример статистической имитационной модели системы со случайными параметрами

Рассмотрим модель процесса самонаведения в вертикальной плоскости летательного аппарата (ЛА) с радиолокационным координатором на некоторый объект (цель), в условиях однократного воздействия помехи типа ложной цели. Целью моделирования является оценка точности системы.

Движение ЛА (в наиболее упрощенном виде) описывается линеаризованной системой дифференциальных уравнений [14]:

, ,

,

, ,

, . (3.33)

В уравнениях (3.33) использованы следующие обозначения переменн

ых состояния модели (рис. 34, 35):  - угол наклона траектории ЛА;  - угол тангажа ЛА; _z - скорость изменения угла тангажа ЛА; _в - угол отклонения рулей высоты ЛА; y_ла - высота ЛА; y_ц - высота цели; D - горизонтальная проекция дальности "ЛА - цель".

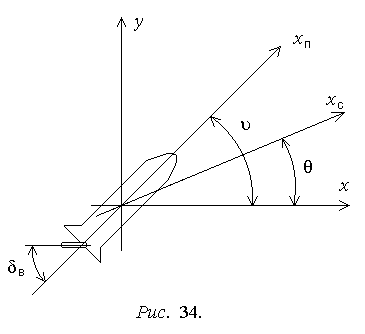
Постоянные коэффициенты и параметры модели: K,L,M,N - аэродинамические коэффициенты; T_рп,k_рп - постоянная времени и коэффициент передачи рулевого привода; v - скорость ЛА; v_цx,v_цy - горизонтальная и вертикальная проекции скорости цели.

Сигнал управления ЛА формируется в виде =_ст+_сн, где _ст=i₁i₂_z - сигнал стабилизации; i₁,i₂ - коэффициенты передачи автопилота; _сн=-k_сн(_к) - сигнал самонаведения по методу погони; k_сн - коэффициент самонаведения; _к - измеренный координатором угол наклона линии визирования цели.

Будем учитывать только детерминированные ошибки измерения, обусловленные наличием ложной цели.

При отсутствии ложной цели угол наклона линии визирования цели измеряется точно:

.

При наличии ложной цели, если в пределах диаграммы направленности антенны координатора находятся обе цели (рис. 35,а), координатор на основе суммарного сигнала измеряет угловое положение некоторого эффективного центра отражения (ЭЦО):

, , y_лц=const,

где s_ц и s_лц - интенсивности радиолокационного сигнала соответственно истинной и ложной целей.

После выхода за пределы диаграммы направленности одной из целей (разрешения целей) координатор измеряет соответственно угловое положение истинной цели (рис. 35,б) _к=_ц или ложной цели (рис. 35,в):

.

Для построения модели процесса наведения с учетом действия рассматриваемой помехи дополним уравнения (3.33) моделью смены дискретных состояний системы управления, выделив их по признаку различия сигнала управления .

Множество состояний будет иметь вид X=(x₁,x₂,x₃,x₄),

где x₁ - наведение на истинную цель: _сн=-k_сн(_ц);

x₂ - наведение на ЭЦО: _сн=-k_сн(_эцо);

x₃ - наведение на ложную цель: _сн=-k_сн(_лц);

x₄ - отсутствие сигнала самонаведения (координатор работает в режиме поиска цели): _сн=0.

Логика смены состояний описывается графом на рис. 36,а и для случая однократного появления ложной цели иллюстрируется схемой на рис. 36,б.

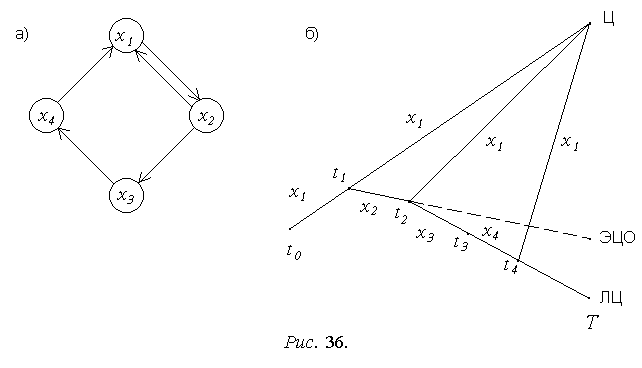
На рис. 36,б отмечены моменты времени: t₀ - начала моделируемого процесса наведения, t₁ - появления ложной цели, t₂ - разрешения целей, t₃ - селекции ложной цели и переключения координатора в режим поиска цели, t₄ - повторного захвата на сопровождение истинной цели, T - окончания процесса наведения.

Таким образом, на интервале времени [t₀;T] могут иметь место следующие последовательности состояний, или фаз движения системы:

u₁: x₁;

u₂: ;

u₃: ;

u₄: ;

u₅: .

Переход из x₁ в x₂ возможен только в момент времени t₁ и происходит с вероятностью p₁₂. Момент t₂ и соответствующий ему переход определяются изменением текущих координат моделируемых объектов. Интервалы времени _t₃-t₂ и _t₄-t₃ - непрерывные случайные величины, распределенные по экспоненциальному закону.

Таким образом, построенная модель реализует схему ДРС (подразд. 2.2). Отметим также, что система (3.33) после подстановки в правую часть четвертого уравнения выражений для  оказывается нестационарной.

Точность системы характеризуется величиной конечной ошибки :

=(T)=y_ц(T)-y_ла(T), (3.34)

где T определяется из условия D(T)=0.

Все параметры модели, включая начальные условия, можно разбить на четыре группы:

1. Детерминированные (фиксированные) параметры, характеризующие элементы системы управления ЛА: K, L, M, N, T_рп, k_рп, v, i₁, i₂, k_сн, s_ц, .

2. Связанный параметр, определяемый в процессе моделирования: _t₂-t₁.

3. Случайные параметры, характеристики распределения которых определяются предшествующими процессами в системе: t₀, начальные условия ₀, ₀, _z0, _в0, y_ла0, D₀, для уравнений (3.33), интервалы _ и _. В эту группу включим также дискретный параметр  с двумя возможными значениями (0 при отсутствии перехода в x₂ в момент t₁ и 1 при наличии такого перехода).

4. Неопределенные параметры, характеризующие исследуемые условия применения системы: y_ц0, v_цx, v_цy, y_лц, s_лц, t₁.

Таким образом, модель является стохастической, и для показателя качества (3.34) могут быть определены только средние характеристики.

Ограничимся оценкой математического ожидания конечной ошибки системы.

В условиях случайности и неопределенности ряда параметров в общем случае могут быть получены условные оценки m_, соответствующие конкретным значениям неопределенных параметров и конкретным законам распределения случайных параметров модели. Рассматриваемая модель нестационарной ДРС допускает только имитационное моделирование.

Пусть для моделируемой ситуации заданы:

- фиксированные значения y_ц0, v_цx, v_цy, y_лц, s_лц, t₁;

- законы распределения случайных параметров, которые считаются статистически независимыми:

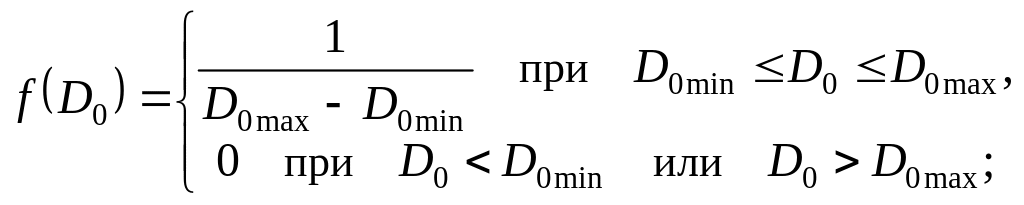
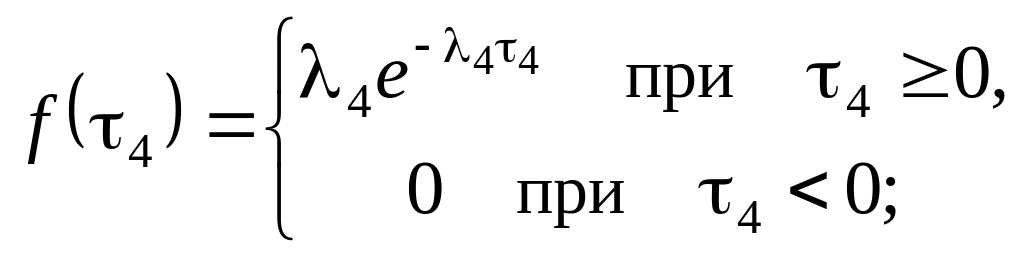
P(=1)=p₁₂, P(=0)=1-p₁₂;

- для остальных случайных параметров фиксированные значения.

Процедура статистического имитационного моделирования и оценки m_ для заданной ситуации будет выглядеть следующим образом.

Должны быть получены n реализаций процесса наведения, начиная с t₀, путем численного интегрирования на ЦВМ модели (3.33) с учетом смены дискретных состояний системы (серия опытов объемом n).

Перед каждым i-м опытом с помощью стандартного генератора случайных чисел , распределенных по равномерному закону в интервале [0;1], "разыгрываются" значения случайных параметров модели:

(D₀)_i=D_0min+(D_0max - D_0min)_4i-3,

,

,

и рассчитывается значение .

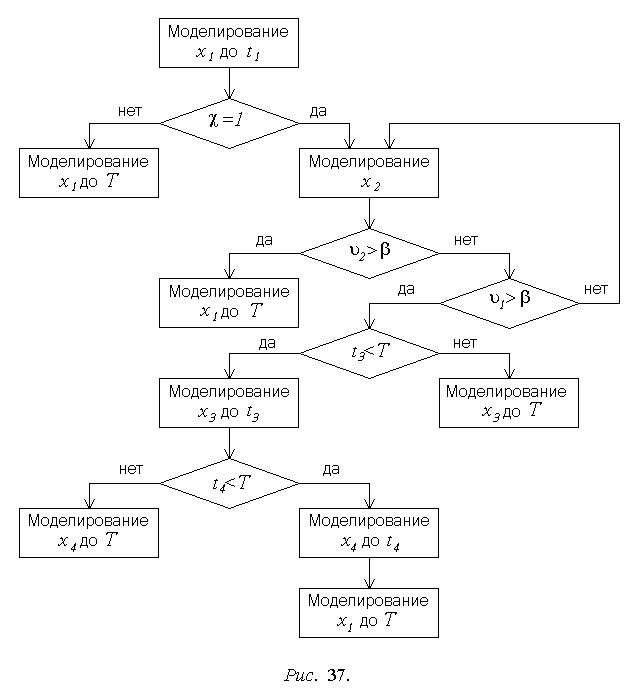
Укрупненная блок-схема получения i-й реализации процесса наведения представлена на рис. 37. В процессе моделирования определяется (t₂)_i, как момент, когда в первый раз окажется выполнено одно из условий: ₁> или ₂> (рис. 35,б,в), - и определяется дальнейшее развитие процесса: переход при ₂> или переход при ₁>. После определения (t₂)_i раcсчитываются (t₃)_i=(t₂)_i+(₃)_i и (t₄)_i=(t₃)_i+(₄)_i. В качестве результата i-го опыта регистрируется _i = y_ц(T_i) - y_ла(T_i)

Оценка математического ожидания конечной ошибки системы определяется как

Необходимое количество опытов n определяется с учетом требуемой точности результата по (3.19) или на основе соответствующего итерационного алгоритма.

Отметим в заключение две особенности реализации такой модели методом статистического моделирования:

- необходимое количество опытов (имитируемых реализаций процесса наведения) не зависит от количества учитываемых случайных параметров модели;

- если требуется оценить показатель качества системы для различных ситуаций, отличающихся исходными данными (разные фиксированные значения параметров или законы распределения), рассмотренная процедура в полном объеме, включая серию опытов, должна быть повторена для каждого варианта исходных данных.