3.5.2. Программные способы построения генераторов случайных чисел

Программные генераторы случайных чисел обеспечивают получение только псевдослучайных последовательностей со всеми указанными выше недостатками. Общий принцип построения программных генераторов состоит в том, что на первом этапе имитируется равномерный закон распределения в интервале [0; 1], а затем полученная последовательность преобразуется для обеспечения требуемых характеристик. Рассмотрим ряд способов построения программных генераторов.

1. Получение равномерного закона в интервале [0; 1] обеспечивается на основе использования рекуррентных соотношений различного вида, например:

, i=1,2,...,

где a,b - положительные числа, m=2^l, l - разрядность представления целого числа в ЦВМ. Генераторы, или датчики, случайных чисел с равномерным законом распределения имеются в виде встроенных процедур во всех языках программирования, позволяющих решать вычислительные задачи. Существует ряд способов проверки качества таких генераторов [23, 37]. Но прежде всего при выборе программных средств для статистического моделирования следует обратить внимание на способ начальной установки генератора и возможности ее изменения.

2. Метод обратных функций, обеспечивающий получение заданного закона распределения, основан на использовании известного результата теории вероятностей: независимо от вида непрерывного закона распределения при известных его ПРВ f(x) и ФРВ F(x) случайная величина

(3.25)

распределена по равномерному закону в интервале [0; 1].

Действительно, в соответствии с (3.25) значения x и R связаны взаимно однозначной зависимостью. Поэтому для любых A и B

, (3.26)

что является свойством равномерного закона распределения.

Если удается получить аналитическое выражение для функции F^-1(R), обратной ФРВ F(x), процедура генерирования случайных чисел x_i будет выглядеть следующим образом:

а) с помощью стандартного генератора получают равномерно распределенные в интервале [0; 1] числа _i;

б) числа x_i получают по формуле x_i=F^-1(_i).

Например, для экспоненциального закона распределения (x>0)

f(x)=e^-x, F(x)=1-e^-x, .

Рассмотренный способ позволяет получать любой непрерывный закон распределения, если только существует аналитическое выражение для F(x) и может быть получена в аналитическом виде обратная функция.

3. Для нормального закона распределения аналитического выражения для ФРВ не существует. Простейший способ получения случайных чисел с нормальным законом распределения основан на центральной предельной теореме. В соответствии с ней среднее арифметическое n равномерно распределенных в интервале [0; 1] случайных чисел имеет асимптотически нормальный закон распределения с математическим ожиданием 0,5 и дисперсией

.

На практике это в достаточной степени подтверждается при n=12.

Поэтому процедура получения нормального закона выглядит следующим образом:

а) с помощью стандартного генератора получают 12 равномерно распределенных в интервале [0; 1] чисел _i;

б) числа x_i со стандартизованным нормальным законом распределения получают по формуле, являющейся следствием (3.5):

, .

Для сокращения трудоемкости этот способ иногда применяют с n=6.

Отметим, что рассмотренным способом не обеспечивается свойственный нормальному закону неограниченный диапазон распределения генерируемых чисел.

От указанного недостатка свободна, например, следующая процедура:

а) с помощью стандартного генератора получают два равномерно распределенных в интервале [0; 1] числа _i и _i+1;

б) вычисляют V₁=2_i–1, V₂=2_i+1–1, s=V₁²+V₂²;

в) если , повторяют пункты а) и б);

г) вычисляют и получают два распределенных по стандартизованному нормальному закону числа x_j =V₁r, x_j+1=V₂r.

4. Для произвольных законов распределения, не допускающих аналитического получения ФРВ, существует универсальный способ (рис. 25), основанный на кусочной аппроксимации функции ПРВ. Рассмотрим его на примере усеченного закона распределения, когда f(x)=0 за пределами отрезка [x_min; x_max]. Разобьем указанный отрезок на m=2^l, (l - целое) интервалов таким образом, чтобы вероятность попадания x в каждый интервал была одинаковой:

, j=1,2,...m; a₁=x_min, a_m+1=x_max.

В пределах каждого интервала ПРВ аппроксимируется константой:

, j=1,2,...m.

Процедура формирования случайных чисел в соответствии с заданной ПРФ f(x) выглядит следующим образом:

а) с помощью стандартного генератора получают равномерно распределенное в интервале [0; 1] число _2i-1;

б) по первым l разрядам _2i-1 выбирают номер интервала j;

в) получают следующее значение _2i;

г) значение x_i вычисляют по формуле x_i=a_j+(a_j+1-a_j)_2i.

Рассмотренный способ обеспечивает получение псевдослучайных чисел с любыми непрерывными или кусочно-непрерывными законами распределения, в том числе задаваемыми таблично. Его недостатками являются сравнительно большие объемы подготовительной работы и используемой оперативной памяти ЭВМ.

5. Отметим другой универсальный способ построения генератора случайных чисел с заданной ПРВ усеченного закона распределения (рис. 26), также часто называемый в литературе методом Неймана. Он предусматривает следующую процедуру обеспечения заданной ПРВ f(x):

а) с помощью стандартного генератора получают пары равномерно распределенных в интервале [0; 1] чисел _2i-1 и _2i;

б) выполняют их преобразование:

x_i=x_min+(x_max–x_min)_2i-1, y_i=f_max_2i; (3.27)

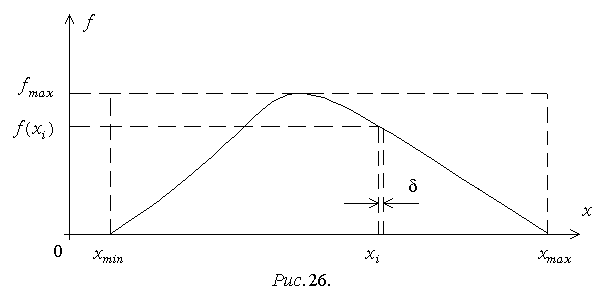
в) в качестве генерируемых значений случайной величины x выбирают значения x_i из тех пар x_i и y_i, для которых выполняется неравенство

. (3.28)

Покажем справедливость данного способа, применительно к его реализации на ЦВМ. Будем рассматривать для каждого x_i элементарную полосу шириной , в пределы которой с учетом разрядности используемой ЦВМ другие значения x попасть не смогут. Величина  достаточно мала, чтобы при законе распределения с ПРВ f(x) вероятность x=x_i можно было считать пропорциональной f(x_i). С учетом свойства равномерного закона (3.26) нетрудно убедиться, что это и будет обеспечиваться при достаточно большой длине генерируемой последовательности на основе условия (3.28).

Преимущество рассмотренного способа - минимальный объем подготовительной работы. Тем не менее он не получил широкого практического применения из-за низкого быстродействия, обусловленного большой долей “безрезультатных” вычислений. Применение этого способа можно порекомендовать только для более сложных задач моделирования случайных векторов со статистически зависимыми составляющими, которые будут рассмотрены в подразд. 3.9.

6. Для формирования случайных чисел с дискретным законом распределения используется выражаемое соотношением (3.26) свойство непрерывного равномерного закона.

Пусть требуется построить генератор дискретной случайной величины Z, имеющей n возможных значений z₁,z₂,…,z_n. Закон распределения Z задается в табличном виде или в виде ряда , где p_j=P(Z = z_j), причем

. (3.29)

Соотношение (3.26) позволяет установить соответствие между значениями непрерывной случайной величины  с равномерным законом распределения в интервале [0; 1] и значениями дискретной случайной величины Z следующим образом. Разобьем интервал [0; 1] на n непересекающихся последовательных отрезков _j, выбрав длину каждого из них равной a_j–a_j-1=p_j. В соответствии с (3.29) эти отрезки полностью займут весь интервал [0; 1] (рис. 27), причем их границы будут определяться соотношениями: .

Теперь достаточно принять Z=z_j, если значение случайной величины  попадает в пределы отрезка [a_j-1; a_j]. Соответствующая процедура получения дискретного закона распределения выглядит следующим образом:

а) с помощью стандартного генератора получают равномерно распределенное в интервале [0; 1] число _i;

б) определяют номер j отрезка _j из условия ;

в) случайной величине Z присваивают значение z_j.

В заключение отметим, что широкий набор разработанных к настоящему времени способов построения генераторов случайных чисел, безусловно, не исчерпывается рассмотренным перечнем. Так для получения нормального и ряда других важных для практических приложений законов распределения в литературе [1, 7, 17, 23, 28, 36, 41, 44, 46] предлагается большой выбор различающихся по точности и трудоемкости специальных способов.