3.3. Точность оценок и определение необходимого количества опытов

Рассмотрим задачу определения вероятности P(А)=p_А случайного события А на основе схемы Бернулли. В соответствии с законом больших чисел и предельными теоремами можно принять (с достоверностью, близкой к 1), что при достаточно больших n оценка этой вероятности p^*_А является непрерывной случайной величиной, распределенной по нормальному закону со следующими математическим ожиданием и среднеквадратическим отклонением:

,

(3.13)

С учетом (3.13) найдем вероятность того, что при определенном n оценка будет отличаться от истинной вероятности не более, чем на :

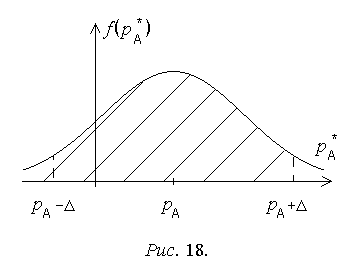
P(|p^*_А – p_A| < ∆) = P(p_A – ∆ < p^*_А < p_A + ∆) = F(p_A + ∆) – F(p_A – ∆), (3.14)

где F(x) - функция распределения вероятностей (ФРВ) случайной величины p^*_А. Графически вероятность (3.14) соответствует заштрихованной площади под кривой ПРВ случайной величины p^*_А (рис. 18).

Соотношение (3.14) обычно представляют в следующей форме:

, (3.15)

г

де

- стандартизованная нормальная случайная величина; определяется по (3.13); P_д - доверительная вероятность;

Доверительная вероятность может быть определена через ФРВ _u стандартизованного нормального закона:

,

где - интеграл вероятностей.

В соответствии с (3.15) модуль абсолютной погрешности p_А-p^*_А оценки вероятности не превосходит с вероятностью P_д.

Таким образом, при достаточно большом n можно с доверительной вероятностью P_д оценить погрешность p^*_А:

(3.16)

или определить количество опытов, необходимое для обеспечения погрешности, не превышающей допустимую _доп.:

. (3.17)

С учетом сказанного очевидно, что после проведения n_треб. опытов нельзя утверждать, что искомая вероятность равна p^*_А. Корректная трактовка результата будет выглядеть следующим образом: с доверительной вероятностью P_д вероятность события А находится в пределах интервала от до . Такой интервал называется доверительным. Некоторые значения P_д и _д(P_д) представлены в табл. 7.

Т а б л и ц а 7

Доверительные вероятности и доверительные интервалы

Pд	0,7	0,75	0,8	0,85	0,9	0,95	0,98	0,99	0,995	0,997
д	1,04	1,15	1,28	1,44	1,65	1,96	2,33	2,58	2,81	3,0

В большинстве случаев P_д выбирают в соответствии с правилом "трех сигм": _д=3, P_д=0,997≈1. Однако если трудоемкость моделирования имеет существенное значение, она может быть уменьшена за счет снижения доверительной вероятности. Так например, при P_д=0,8 _д=1,28, и для обеспечения той же _доп. потребуется в раз меньше опытов, чем при P_д=0,997.

Для оценки математического ожидания (3.2) путем усреднения результатов n опытов в соответствии с законом больших чисел и центральной предельной теоремой аналогично (3.16), (3.17) можно получить:

,

где m_x - математическое ожидание оценки, совпадающее с истинным математическим ожиданием исследуемой случайной величины x; - среднеквадратическое отклонение оценки; D_x – дисперсия случайной величины x.

При достаточно большом n погрешность m_x-m^*_x удовлетворяет неравенству:

, (3.18)

а количество опытов, необходимых для обеспечения допустимой погрешности _доп., равно:

. (3.19)

Отметим следующие особенности полученных результатов:

1. Из соотношений (3.16)-(3.19) хорошо видна "цена" точности статистического моделирования. Повышение точности в m раз требует увеличения количества опытов в m² раз.

2. Определяемое по (3.17), (3.19) количество опытов не гарантирует требуемую точность |_доп.. В строгом смысле никакое конечное количество опытов не может обеспечить такой гарантии, так как, с одной стороны, соотношения (3.16)-(3.19) соответствуют определенной доверительной вероятности P_д<1, и с другой стороны, все полученные результаты основаны на теоретических соотношениях, справедливых для конечных n только с некоторой вероятностью.

3. В формулах (3.16)-(3.17) употребляется значение истинной вероятности p_А, которое в рассматриваемой задаче заведомо неизвестно. В формулах (3.18), (3.19) применяется значение дисперсии D_x, которое также естественно предположить неизвестным. Следовательно, прямое использование соотношений (3.16)-(3.19) невозможно.

На практике эта проблема решается двумя способами.

Наиболее простой состоит в подстановке в (3.17) и (3.19) некоторых возможных значений p_А и D_x, которые позволяют получить точность не хуже требуемой.

Д

ля задачи оценки вероятности при фиксированной _доп. зависимость n_треб.(p_А) имеет максимум при p_А=0,5 (рис. 19). Следовательно, при выборе априорного значения p_А=0,5 и в соответствии с (3.17) будет проведено опытов.

В задаче оценки математического ожидания для D_x априорно принимается некоторая экспертная оценка, соответствующая наибольшему ее возможному значению в рассматриваемой задаче.

При таком способе использования (3.17) и (3.19) для любого окончательного результата будет обеспечена точность не хуже заданной. Недостаток этого способа состоит в том, что трудоемкость эксперимента оказывается завышенной. Так например, если истинное значение p_А=0,9, n_треб. окажется завышенным в раза.

Если трудоемкость эксперимента имеет существенное значение, применяются итерационные алгоритмы получения оценок. Идея итерационных алгоритмов состоит в том, что определение точности и требуемого количества опытов проводится в ходе эксперимента на основе получаемых оценок искомых параметров.

Укрупненная блок-схема простейшего итерационного алгоритма приведена на рис. 20. Для задачи оценки вероятности алгоритм предусматривает:

1

. Проведение начальной серии опытов объемом n и регистрацию количества случаев появления события A n_А.

2. Вычисление оценки вероятности:

.

3. Получение оценки требуемого количества опытов:

.

4. Проведение дополнительной серии опытов объемом n'=n^*_трееб –n и регистрацию количества случаев появления события A n'_А.

5. Уточнение оценки вероятности:

.

6. Оформление окончательных результатов.

Для задачи оценки математического ожидания случайной величины x предусматривается:

1. Проведение начальной серии опытов объемом n и накопление сумм:

, ,

где x_i - реализации случайной величины x в отдельных опытах.

2. Вычисление оценок математического ожидания m^*_x и дисперсии D^*_x :

, . (3.20)

3. Получение оценки требуемого количества опытов:

.

4. Проведение дополнительной серии опытов объемом n'=n^*_трееб –n и накопление сумм:

, .

5. Уточнение оценок математического ожидания m^*_x и дисперсии D^*_x :

, .

6. Оформление окончательных результатов.

Отметим, что использование для оценки дисперсии соотношения (3.20), эквивалентного (3.9), исключает необходимость хранения всей получаемой в ходе эксперимента выборки значений x₁,x₂,…,x_n,… и снижает требования к объему памяти применяемых вычислительных средств.

Рассмотренный способ получения оценок на основе итерационных алгоритмов обеспечивает некоторое снижение трудоемкости статистического моделирования, но также не свободен от недостатков.

Основная проблема здесь связана с тем, что результаты проводимых серий опытов складываются случайным образом и при конечных n возможны следующие эффекты:

1. Выборочный закон распределения может существенно отличаться от нормального.

2. Разброс составляющих выборку реализаций случайной величины может оказаться существенно меньше истинного ее разброса.

3. В выборке могут оказаться реализации случайной величины, значительно отличающиеся от ее среднего значения, в непропорционально большом количестве.

В первом случае соотношения (3.16)–(3.19) дадут неточные результаты. Чаще всего оценки требуемого количества опытов оказываются завышенными.

Во втором случае оценки требуемого количества опытов при использовании итерационных алгоритмов оказываются резко заниженными, а результаты моделирования – неточными. Во избежание подобных ситуаций рекомендуется выбирать объем начальной серии опытов не менее 100-500.

В третьем случае возможны завышенные оценки требуемого количества опытов с получением неточных результатов моделирования. Обнаружить такие ошибки можно только на основе независимого контрольного моделирования, например, с помощью других генераторов случайных чисел или с изменением их начальной установки.

Практика использования итерационных алгоритмов получения оценок позволяет рекомендовать в качестве наиболее надежного способа решения указанных проблем переход к интерактивным алгоритмам, предоставляющим пользователю необходимую информацию и возможность управления объемами дополнительных серий опытов.

Отметим также, что для малых выборок, например n≤30, в математической статистике разработаны более точные способы определения допустимых (толерантных) интервалов значений оценки и соответствующих доверительных вероятностей, свободные от гипотезы о нормальном законе ее распределения [12, 35, 43].