9.11.2. Управление автономной системой

Рассмотрим метод решения задач оптимального управления при отсутствии ограничений на фазовые координаты. Система (9.75) называется автономной, если в ее правую часть явно не входит время t.

Пусть в фазовом пространстве Х заданы две точки x⁰ = ( ) и x¹ = (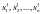 ). Если начальное и конечное положения изображающей точки в фазовом пространстве определены по всем n координатам, то задачу об оптимальном управлении называют задачей с закрепленными концами.

Рассмотрим следующую задачу. Требуется среди допустимых управлений u(t), t₀ ≤ t ≤ t₁, т.е. кусочно-непрерывных вектор-функций u(t) U (моменты t₀ и t₁ не фиксированы), переводящих фазовую точку системы (9.75) из заданного начального положения x⁰ (x(t₀) = x⁰) в заданное конечное положение x¹ (x(t₁) = x¹), найти управление и траекторию при ограничениях вида (9.76) или (9.77), минимизируя при этом функционал

i = 1:n, j = 1:m.

Управление u(t) и траектория х(t), решающие поставленную задачу, называются оптимальными.

Особое внимание уделяется частному случаю, когда f₀ = 1. В этом случае функционал

задает время движения. Управление и траектория, минимизирующие функционал, называются оптимальными по быстродействию.

Уравнения Эйлера (9.10) представляют собой систему n уравнений второго порядка. Такую систему всегда можно свести к системе 2n уравнений первого порядка. Наиболее удобны уравнения Эйлера в так называемой форме Гамильтона.

Введем новые переменные

(9.80)

и функцию

, (9.81)

где ψ_i – канонические переменные, H – функция Гамильтона.

Из выражения (9.81) следует, что

, i = 1:n (9.82)

Уравнения Эйлера (9.10) перепишутся в виде

, i = 1:n. (9.83)

Из выражения (9.81) также следует

, i = 1:n. (9.84)

Объединяя уравнения (9.83), (9.84) получаем так называемую Гамильтонову форму уравнений Эйлера (2n уравнений Эйлера-Гамильтона)

(9.85)

Пример 9.8. Рассмотрим двигатель КПДН-3-V с независимой обмоткой возбуждения. Мощность двигателя — 8,5 кВт; номинальная скорость вращения — 1300 об/мин = 21,6 об/с, маховой момент двигателя CD² равен 1 кГ∙м²; номинальный ток — 45 А; допустимая кратность тока 3,6; допустимая скорость вращения — 1560 об/мин, т. е. 1,2 от номинальной скорости. Двигатель через редуктор приводит во вращение исполнительный механизм, причем для отработки полного цикла перемещения двигатель должен повернуться на 130 радиан.

Решение. С учетом момента инерции исполнительного механизма механическая постоянная времени электропривода Т_м = 0,7 с, следовательно, единицей угла перемещения будет

α₀ = 2π·21,6·0,7 = 95 рад,

таким образом, заданный для отработки в течение цикла угол перемещения будет равен:

α = 130/95 = 1,35.

Цикл перемещения должен занимать 2 с, число циклов — 1000 в час, т. е. 2 с продолжается работа двигателя и 1,6 с — пауза. Момент сопротивления, приведенный к валу двигателя, М_с = 3,2 кГ∙м, в то время как номинальный момент двигателя

М_н = 975·8,5/1300 = 6,4 кГ∙м,

т.е. µ₀ = 0,5. Требуется определить, способен ли выбранный двигатель обеспечить заданный темп работы и каковы параметры оптимальной диаграммы тока.

Вычисляем Т :

Т = 2/0,7 = 2,86;

в то время как допустимая величина для Q (принимая условия охлаждения во время работы и во время паузы одинаковыми)

Q_доп = 3,6/2 = 1,8.

Следовательно, выбранный нами двигатель при оптимальном законе управления удовлетворяет ограничениям по нагреву, тогда как при законе управления ί — const мы имели бы

т. е. нагрев двигателя превысит допустимый, и потребуется установка более мощного двигателя.

Произведем проверку оптимального закона на величину максимального тока и максимальной скорости в режиме оптимального управления.

Имеем:

следовательно, максимальный ток якоря в начале цикла будет составлять i₀ + µ₀ = 1,5, т. е. будет меньше допустимого. Максимальная скорость вращения

т. е. также меньше допустимой.

Изменим условия. Пусть тот же двигатель должен за 2 с отработать перемещение 238 рад, т. е. α = 2,5.

В этом случае в режиме оптимального управления имеем:

Однако

что превышает допустимую скорость. Следовательно, необходимо перейти на режим управления с участком постоянной скорости. Параметры оптимальной диаграммы определяем по формулам:

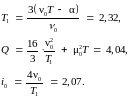
Таким образом, максимальный ток i_max = i₀ + µ₀= 2,57, что допустимо. Окончательно, при оптимальном управлении Q = 4,04, т. е. длительность паузы должна составлять 3,04 от длительности работы и допустимое число включений в час

Пример 9.9. Рассмотрим двигатель, разгоняющий механизм, который имеет большой маховой момент, равный 12,08∙10⁴ кГ∙м²; момент сопротивления механизма— 244 кГ∙м, скорость вращения — 600 об/мин.

Так как наименьшие тепловые потери будут в том случае, когда момент двигателя, разгоняющего механизм, будет равен удвоенному моменту сопротивления, выберем двигатель с моментом Μ = 488 кГ∙м, что при двукратной перегрузочной способности будет соответствовать номинальному моменту М_н = 244 кГ∙м и номинальной мощности

и, следовательно, время разгона исполнительного механизма от нуля до номинальной скорости будет равно 790 с или 13,2 мин (в данном случае время разгона равно механической постоянной времени, т.е. Т = 1).

Определим величину перегрева двигателя в конце цикла разгона. Для двигателя мощностью 150 кВт постоянная времени нагрева составляет 45 мин, т. е. n = 13,2/45 = 0,294. Следовательно, в конце разгона перегрев обмоток

т. е. будет на 2,4% превосходить нормальный перегрев обмоток в длительном режиме при номинальном токе. Такой перегрев является вполне допустимым.

Так как в данном случае ввиду очень большой величины маховых масс процесс разгона протекает медленно и множитель е^-nτ уже заметно отличается от единицы, то при выборе закона управления имеет смысл учитывать теплоотдачу. Оптимальная диаграмма тока будет иметь вид:

Задавшись условием, что в конце цикла разгона перегрев обмоток должен быть равен номинальному, получим два уравнения для определения Т и i₀:

Решив систему, получим: Т = 0,82; i₀ = 2,45. Следовательно, ток якоря в начале разгона равен 2,45 от номинального, а в конце разгона 1,92 от номинального; время разгона будет 0,82·3,2 = 10,8 мин, или на 18% меньше, чем при прямоугольной диаграмме тока.