318

9. Теория оптимального управления

9.1. Определения

На рис. 9.1. показана общая структурная схема управления, состоящая из двух звеньев 1 и 2. Звено 1 называется управляющим органом или управляющим устройством. Оно должно прежде всего обеспечивать цель управления. Звено 2 называется объектом управления. Под термином «объект управления» будем понимать не только машины и механизмы, но и целые производственные процессы.

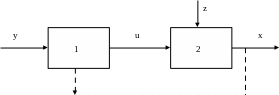
Рис. 9.1. Структурная схема системы управления

Задачу оптимального управления можно представить в виде составного объекта (рис. 1.1): цель управления, управляемый объект, измерительную систему и вычислительное устройство, осуществляющее расчет оптимального управления.

Задача вычислительного устройства – найти связи между вектором состояния в конечный момент времени х_к, вектором управления u и измеренным вектором состояния х_изм.

При решении задачи оптимизации необходимо вначале выбрать и сформулировать цель (выбрать критерий оптимальности), затем согласовать ее с имеющимися возможностями (учесть ограничения) и, наконец, реализовать способ достижения цели при учете ограничений.

Предполагается, что состояние исследуемого объекта управления в каждый момент времени t на отрезке 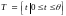однозначно характеризует n действительными числами x₁(t), x₂(t),…, x_n(t) или вектор – функцией x(t) = (x₁,…, x_n) в пространстве Eⁿ, которое будем называть фазовым пространством или пространством состояний объекта. Изменение вектора состояния во времени будем называть движением объекта в (n+1)–мерном пространстве позиций 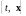. Составляющие вектора x могут иметь самую различную природу и сущность: для генератора − напряжение, мощность и частота; для предприятия − отдельные показатели плана. На составляющие вектора х могут и почти всегда накладываются ограничения типа

х₁≤Х₁, х₂≤Х₂,…, х_n≤Х_n.

Допустим, мощности всех машин, аппаратов, предприятий и даже целой страны на некотором отрезке времени всегда ограничены. Нарушение этих ограничений обычно приводит к ненормальным и опасным режимам.

К объекту управления приложены воздействия: управляющие, которые могут быть охарактеризованы некоторой вектор – функцией u(t) = (u₁, u₂,…, u_k), называемой управлением, и возмущающие, представляемые вектор –функцией z(t) = (z₁, z₂,…, z_l).

Управляющие воздействия − это воздействия, которые сознательно меняются для достижения цели управления. На составляющие вектора u накладываются ограничения типа

u₁≤U₁, u₂≤U₂,…, u_k≤U_k.

Если взять синхронный генератор, то напряжение возбуждения, с помощью которого управляют напряжением на статоре, не может превосходить паспортных данных.

Управляющий орган характеризуется прежде всего способностью вырабатывать вектор u. Изменение вектора u во времени или в пространстве координат (u₁, u₂,…, u_k) называется алгоритмом управления. Таким образом, управляющее устройство выдает на объект управления алгоритм в виде изменения вектора u. В свою очередь устройство управления получает внешние команды y, служащие для запуска и перестройки управляющего устройства.

На объект управления могут также действовать возмущающие воздействия, которые, как правило, искажают алгоритм управления u, мешают достижению цели управления, поэтому они называются часто помехами.

Некоторые составляющие вектора z могут быть полезными, т.е. такими, для преодоления которых и предназначен объект, например преодоление полезного момента двигателем. Возмущающие воздействия в большинстве случаев не подвластны человеку и зачастую можно говорить о характере их изменения только в статистическом смысле.

Если детально изучить составляющие вектора z, то, очевидно, найдутся ограничения типа выше указанных.

Векторы x, u, z связаны обычно некоторой закономерностью. Рассматриваются только такие объекты, в которых связь между векторами может быть записана в виде системы обыкновенных дифференциальных уравнений

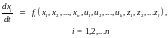(9.1)

или в векторной форме

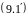
где функции f_i определены для любых значений х, принадлежащих некоторой области х Х, и любых значений u, принадлежащих области управления u U. Области X и U могут быть открытыми и замкнутыми. Функции f_i непрерывны по совокупности x₁, x₂,…, x_n и непрерывно дифференцируемы по x₁, x₂,…, x_n. Вектор u может быть функцией непрерывной, кусочно-непрерывной или кусочно-гладкой.

Управляющее устройство может получать информацию о векторах x и z и на основе этого формировать вектор u, а может и не получать никакой информации об объекте управления. В первом случае имеется замкнутая система управления, во втором − разомкнутая. В технике нашли применение оба вида систем, но замкнутые распространены гораздо больше. Разомкнутые системы работают по жесткому алгоритму, т.е. являются системами детерминированными. В замкнутых системах алгоритм может меняться в зависимости от значений векторов x и z. Такие системы иногда называются информационными.

Охарактеризовав систему автоматического управления (САУ), следует определить цель управления, т.е. ради чего создается система управления.

В самом общем виде цель управления определяется некоторым функционалом

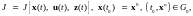(9.2)

где G₀ − некоторая ограниченная область пространства позиций; t₀ − начальный момент времени. Требуется найти такой алгоритм u(t) или u = f (x,z), при котором функционал (9.2) принимал бы экстремальное значение, т.е.

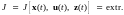
При определении функционала, естественно, должны учитываться ограничения, накладываемые на u, z:

z(t) Z, u(t) U, t T, (9.3)

отражающие особенности задачи. В частном случае, это могут быть ограничения отклонения рулей, энергетических режимов, ограничения на допустимые условия эксплуатации системы и т.д.