Реальные импульсы

Выше предполагалось, что входной сигнал восстанавливающего фильтра представляет собой последовательность взвешенных дельта-импульсов

Такую последовательность реализовать невозможно. Поэтому практически формируется сигнал, определяемый выражением

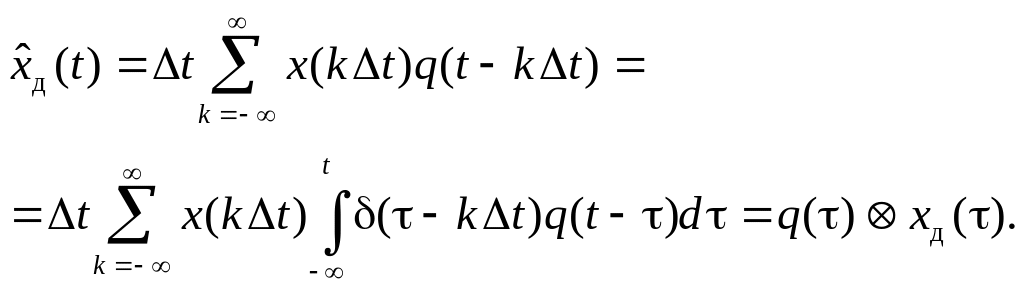
где произвольная функция. Выбор определяется тем, насколько легко ее можно реализовать. Выражение можно рассматривать как выход некоторого фильтра с импульсной характеристикой на вход которого подан сигнал . С учетом этого на рис. 2.5.14 представлена блок-схема восстановления.

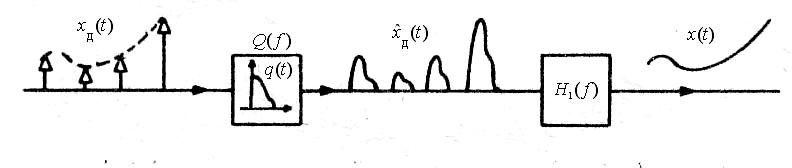
Рис. 2.5.14

Характеристика восстанавливающего фильтра выбирается с учетом реальных импульсов и должна удовлетворять соотношению

где

а функция, выбранная так, чтобы имело место

Например, может быть выбрана в соответствии с . Тогда

Пример 2.5.4. Пусть

Спектр этой функции

Чтобы удовлетворить первому условию (2.5.2), необходимо положить

В диапазоне частот, для которых с учётом того, что

будем иметь

Такую характеристику нетрудно реализовать (рис. 2.5.15)

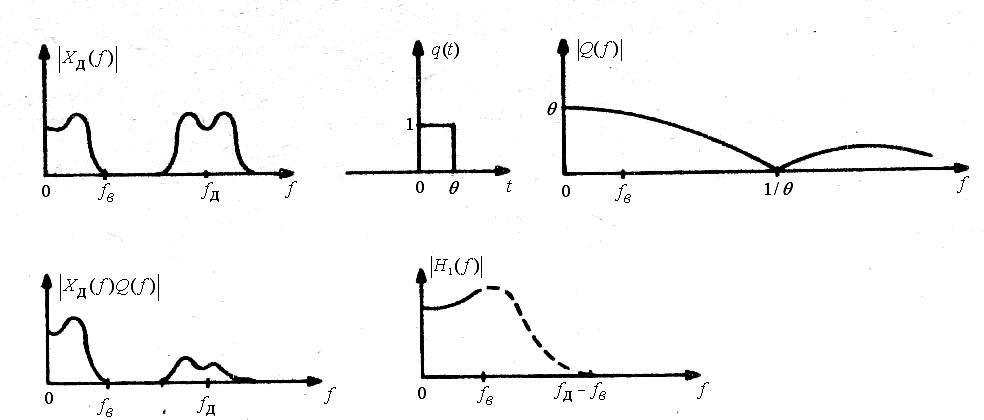
Рис. 2.5.15

2.6. Восстановление сигналов по дискретным отсчётам путём интерполяции

Точное восстановление аналогового сигнала по его дискретным отсчётам предполагает, что имеет финитный спектр, а фильтр восстановления является идеальным. Практический способ восстановления основывается на аппроксимации функции некоторым полиномом, который совпадает с при

Например, можно разложить в ряд между моментами и :

где

Поскольку единственная информация о – её значения в дискретные моменты времени, то производные должны оцениваться по этим значениям:

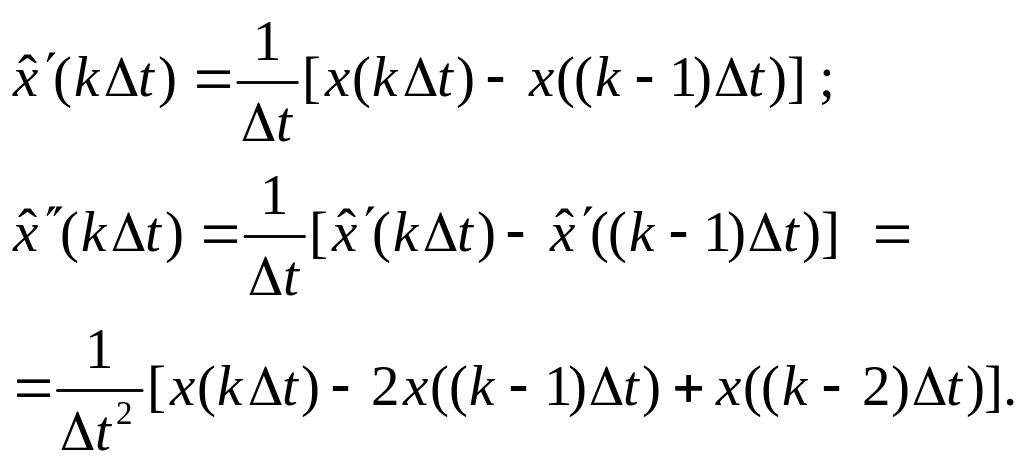
Видно, что чем выше порядок производной, тем большее число предшествующих выборок требуется. Можно легко убедиться, что число предшествующих выборок, необходимых для оценки значения равно Таким образом, описанный метод аппроксимации предполагает, что имеется набор временных задержек, число которых зависит от точности аппроксимации. Наличие временного запаздывания всегда нужно учитывать. Так, например, хорошо известно его влияние на устойчивость систем управления с обратной связью. Кроме того, использование производных более высокого порядка неизбежно влечёт за собой более сложные схемотехнические решения. По этой причине ограничиваются несколькими первыми членами ряда .

Ступенчатая интерполяция

В этом случае для аппроксимации сигнала между двумя последовательными выборками используется только первый член . Ступенчатая интерполяция заключается в сохранении величины выборки в пределах шага дискретизации (рис. 2.6.1)

Фиксатор нулевого порядка

У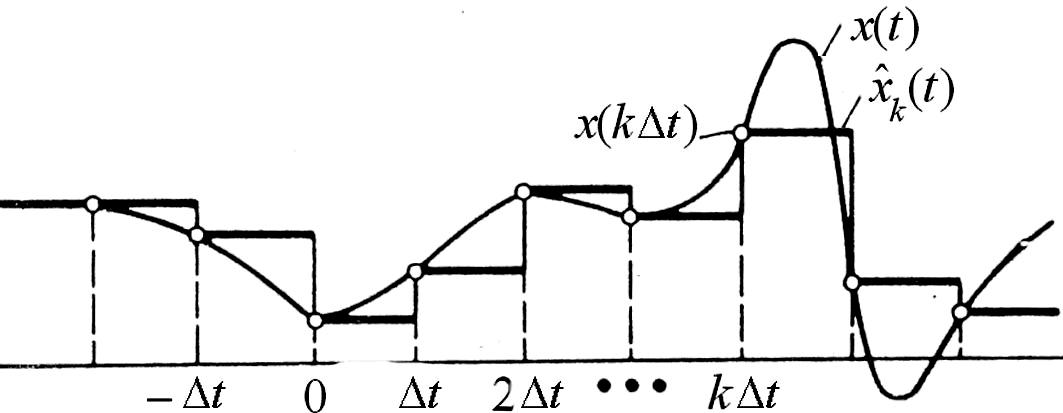 стройство, реализующее такую операцию, называется фиксатором нулевого порядка (рис. 2.4.5В). С интервалом происходит кратковременное замыкание ключа, и в этот момент конденсатор просто «запоминает» отсчётное значение сигнала (рис. 2.6.1)

.

Рис. 2.6.1. Ступенчатая интерполяция

В соответствии с :

Это выражение определяет импульсную реакцию фиксатора нулевого порядка. Частотная характеристика, связанная с импульсной реакцией преобразованием Фурье, будет равна

Обе характеристики фиксатора нулевого порядка приведены на

рис. 2.6.2б, в. Из рисунка видно, что фиксатор нулевого порядка обладает свойствами низкочастотного фильтра. Однако в отличие от идеального восстанавливающего фильтра амплитудно-частотная характеристика фиксатора обращается в нуль при вместо того, чтобы резко спадать до нуля при Непостоянство частотной характеристики в информационной полосе и наличие боковых лепестков в также ухудшают его фильтрующие свойства. Поэтому на выходе фиксатора часто включают дополнительный ФНЧ, например, фильтр в виде интегрирующей цепочки с постоянной времени

Точность фиксатора нулевого порядка существенно зависит от частоты дискретизации.

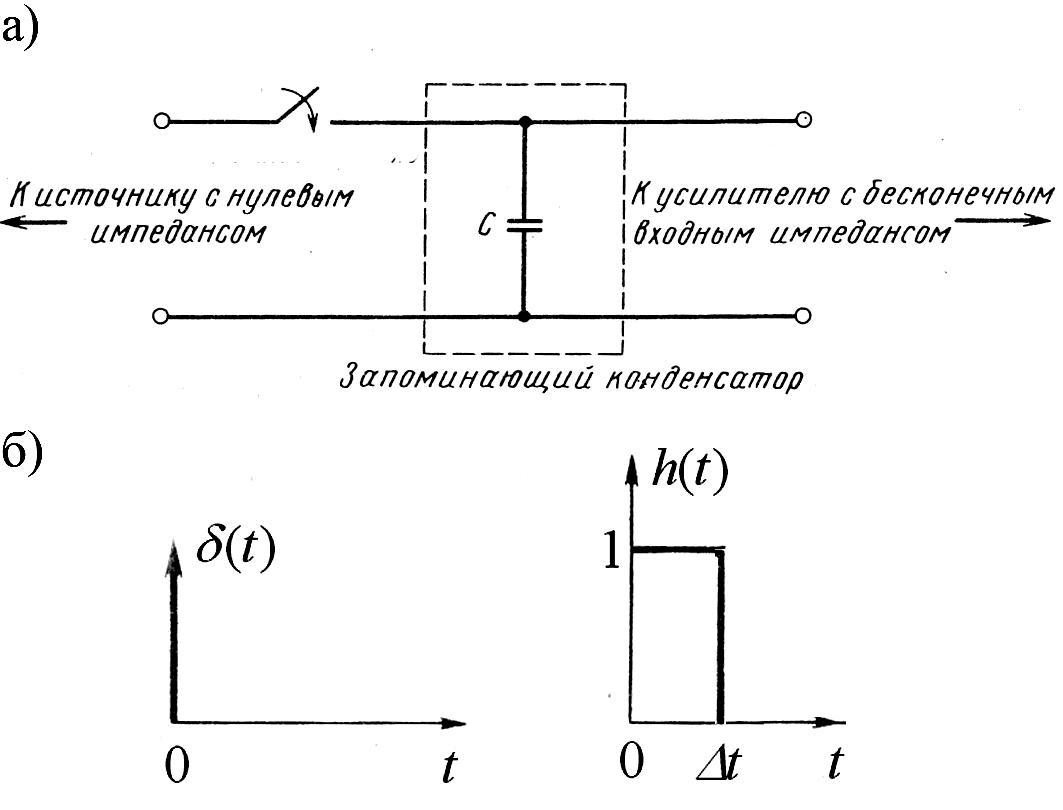
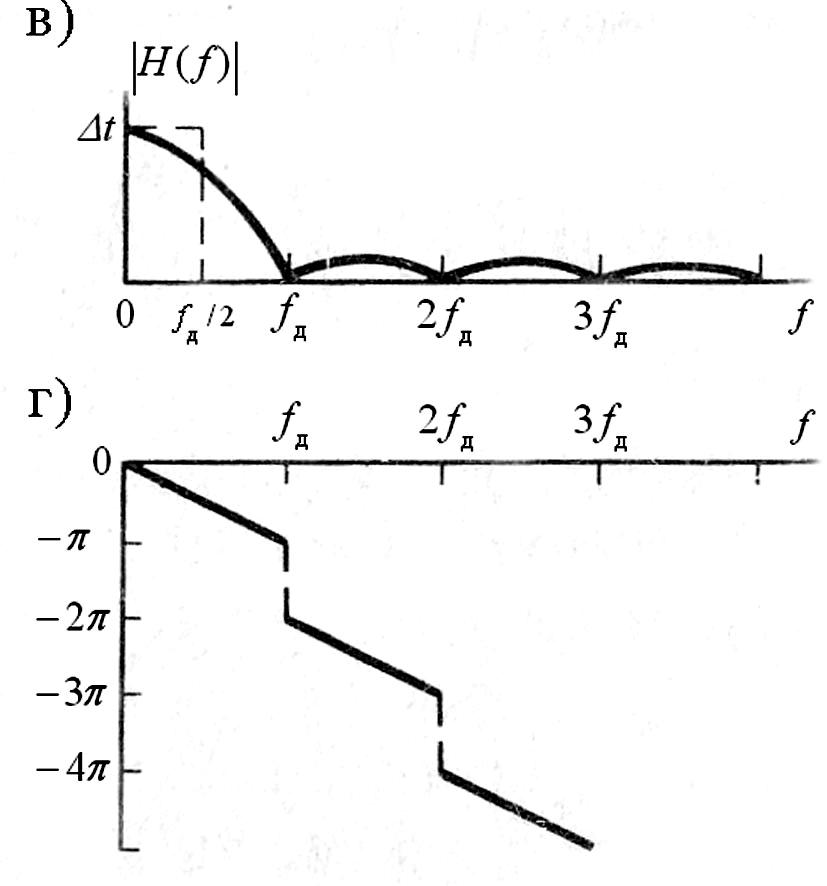
Рис. 2.6.2. Характеристики фиксатора нулевого порядка

Чтобы получить структурную схему фиксатора нулевого порядка, перепишем в следующем виде:

З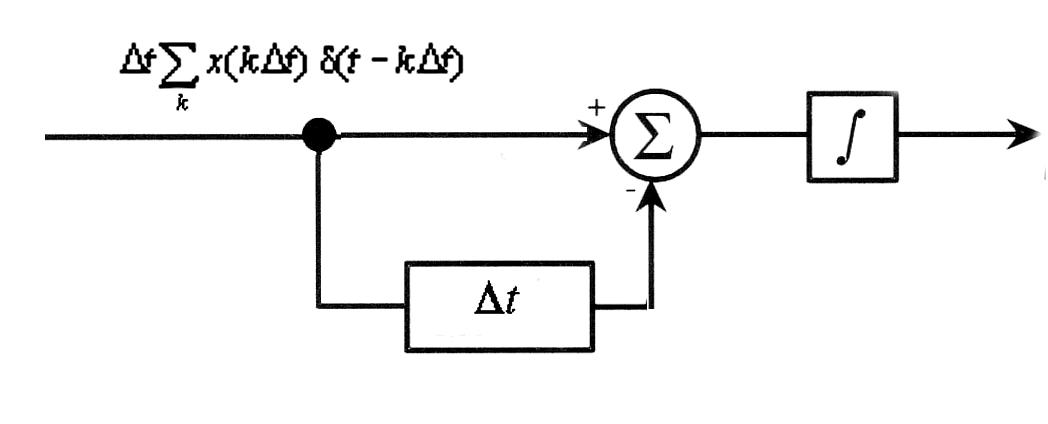 десь частотная характеристика устройства задержки на время а частотная характеристика интегратора. Таким образом, фиксатор нулевого порядка может быть реализован посредством устройства задержки на вычитающего устройства и интегратора, как показано на рис. 2.6.3.

Рис. 2.6.3. Блок-схема фиксатора нулевого порядка