- •Белорусский национальный технический университет
- •Методическое пособие
- •3Семестр
- •Типовой расчет к задаче 1
- •Типовой расчет к задаче 1
- •Литература основная литература
- •Дополнительная литература
- •Примечание.
- •Экзаменационные вопросы по курсу «Теория электрических цепей»
- •1.Электрические цепи постоянного тока.
- •2. Электрические цепи однофазного синусоидального тока.
- •3. Трехфазные электрические цепи.
Белорусский национальный технический университет
МЕЖДУНАРОДНЫЙ ИНСТИТУТ ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
Кафедра «Информационные системы и технологии»
Методическое пособие
к выполнению контрольной работы
по курсу “Теория электрических цепей”
3Семестр
для студентов групп 417218, 417228, 417418, 417428
Минск 2009
З а д а ч а 1.
1.Для электрической цепи, схема которой изображена на рисунках 1.1. - 1.27, составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях цепи (в общем виде);
2.В исходной цепи с двумя источниками ЭДС принять сопротивление R5 и для полученной цепи:
а) определить токи во всех ветвях методом двух узлов;
в) составить баланс мощности;
г) построить потенциальную диаграмму для замкнутого контура, включающего обе ЭДС.
Указания к выбору варианта: две последние цифры номера зачетки (после наклонной черты) определяет номер схемы (рисунок 1.1 - 1.27)
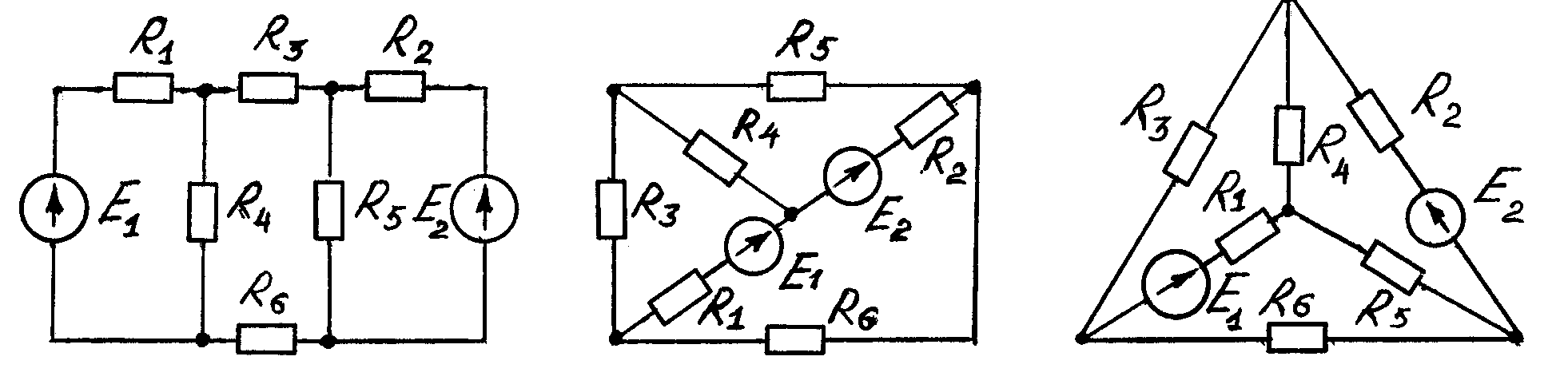 Рисунок 1.1
Рисунок 1.2 Рисунок 1.3
Рисунок 1.1
Рисунок 1.2 Рисунок 1.3
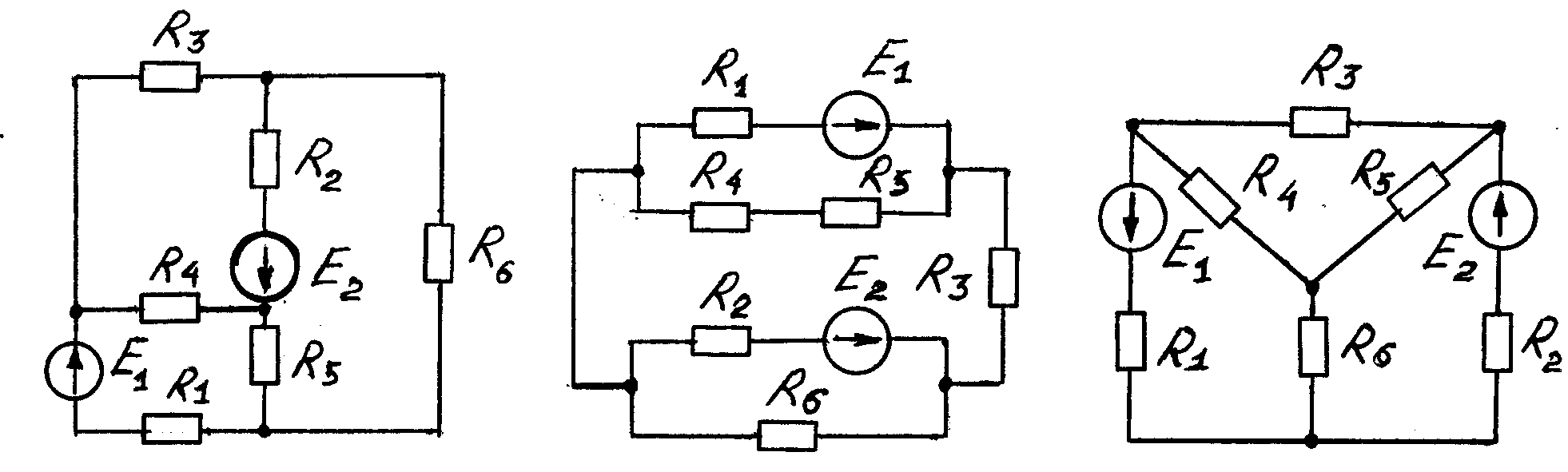 Рисунок 1.4
Рисунок 1.5 Рисунок 1.6
Рисунок 1.4
Рисунок 1.5 Рисунок 1.6
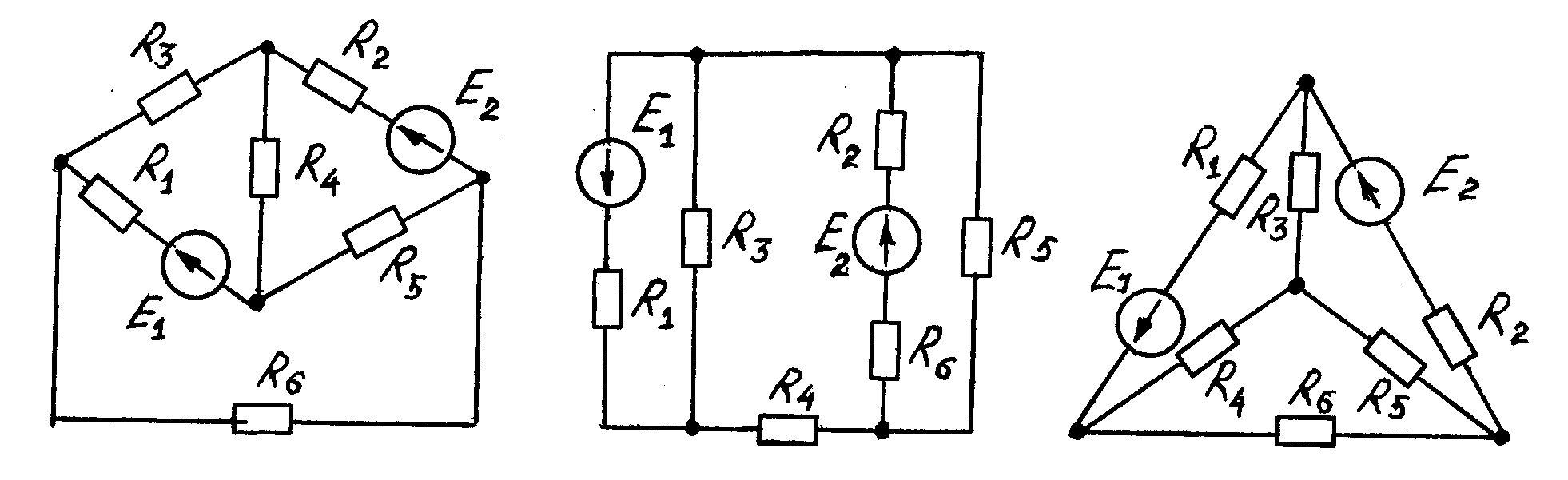 Рисунок 1.7
Рисунок 1.8 Рисунок 1.9
Рисунок 1.7
Рисунок 1.8 Рисунок 1.9
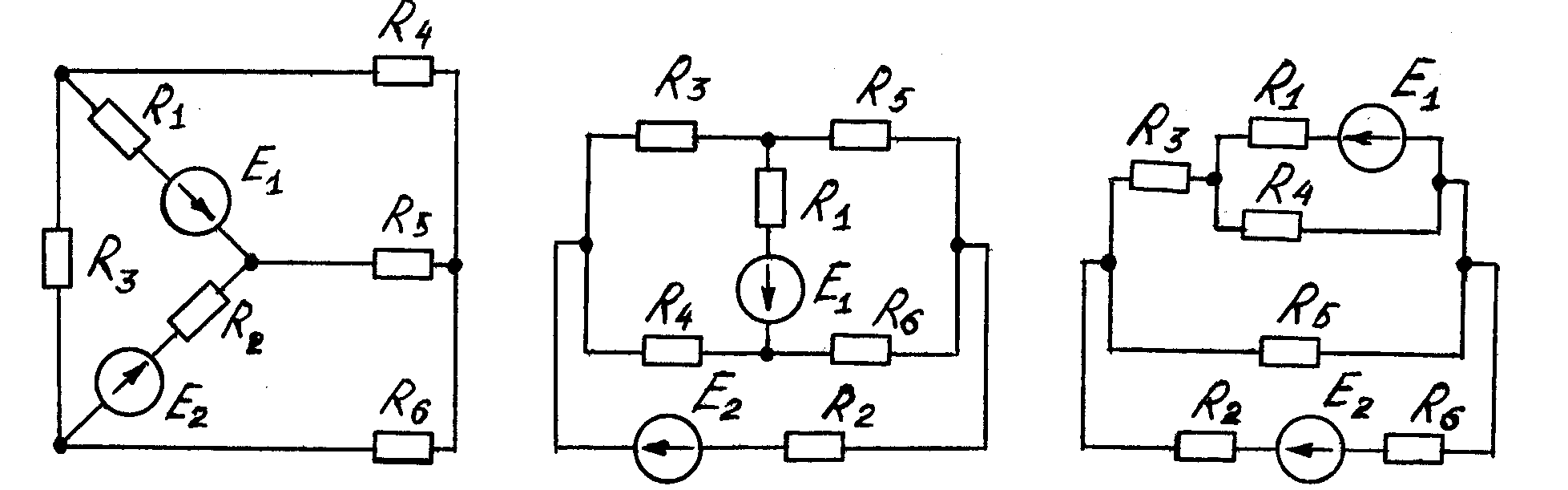 Рисунок 1.10
Рисунок 1.11 Рисунок 1.12
Рисунок 1.10
Рисунок 1.11 Рисунок 1.12
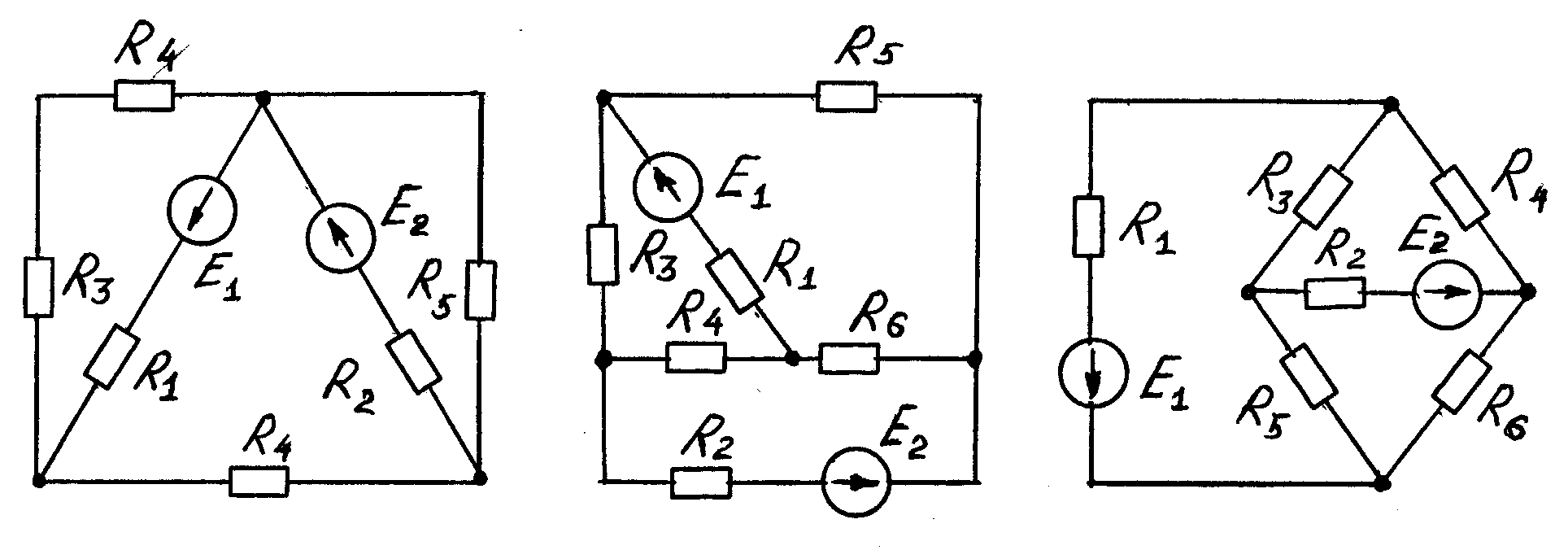 Рисунок
1.13 Рисунок 1.14 Рисунок
1.15
Рисунок
1.13 Рисунок 1.14 Рисунок
1.15
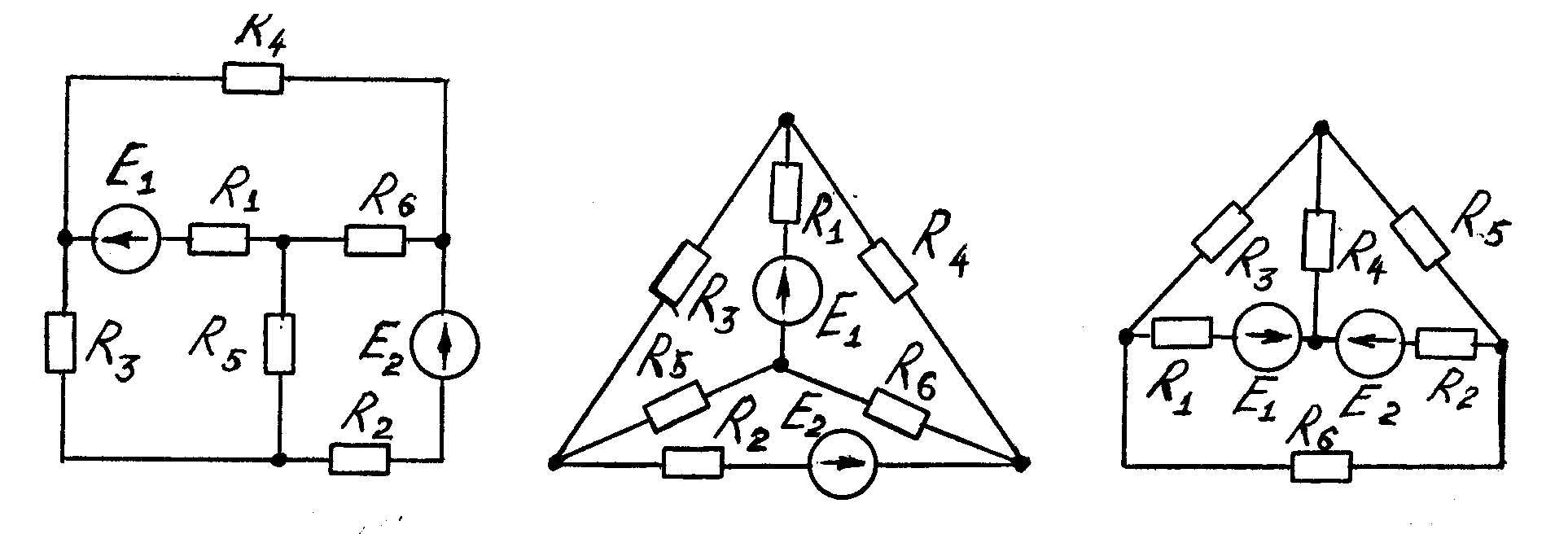 Рисунок 1.16
Рисунок 1.17 Рисунок 1.18
Рисунок 1.16
Рисунок 1.17 Рисунок 1.18
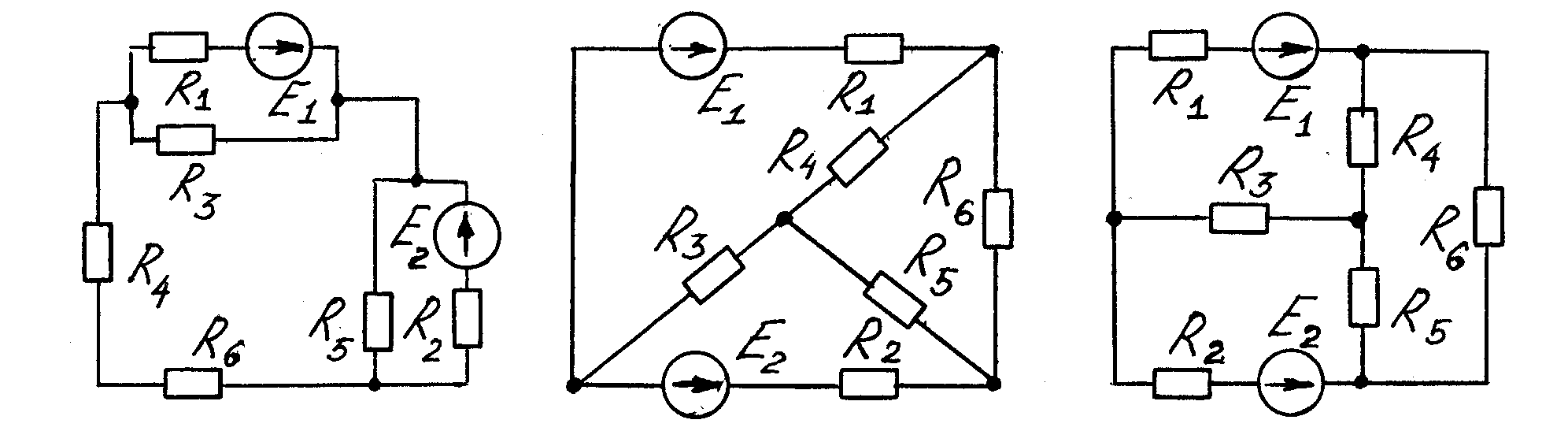 Рисунок 1.19
Рисунок 1.20 Рисунок 1.21
Рисунок 1.19
Рисунок 1.20 Рисунок 1.21
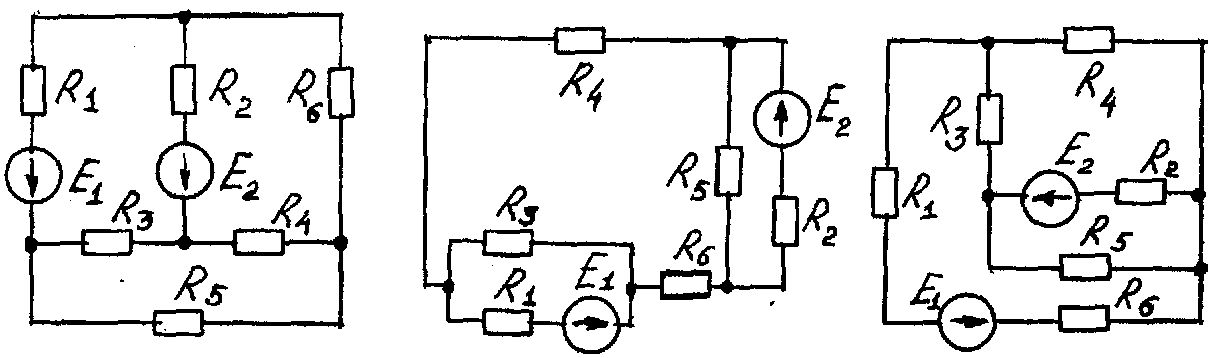
Рисунок 1.22 Рисунок 1.23 Рисунок 1.24
 Рисунок 1.25
Рисунок 1.26 Рисунок 1.27
Рисунок 1.25
Рисунок 1.26 Рисунок 1.27
Таблица 1
Е1, В |
Е2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
200 |
300 |
64 |
43 |
31 |
25 |
54 |
14 |
Типовой расчет к задаче 1
Пример1.Для электрической цепи, схема которой изображена на рисунке 1.28, составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях цепи.

Решение: Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю
![]() .
.
Второй закон Кирхгофа: алгебраическая сумма ЭДС в любом замкнутом контуре электрической цепи равна алгебраической сумме падений напряжения на всех участках контура
![]() .
.
В общем случае токи сложной электрической цепи могут быть определены в результате совместного решения уравнений, составленных по первому и второму законам Кирхгофа. Количество уравнений (m) должно быть равно количеству неизвестных токов цепи. В любой цепи сколько ветвей, столько и токов.
Порядок расчета:
1) произвольно намечают направления токов ветвей и обозначают их. Если цепь имеет n узлов, то по первому закону Кирхгофа записывают (n-1) уравнений, так как уравнение для n-го узла является следствием предыдущих;
2) произвольно намечают направления обхода контуров и по второму закону Кирхгофа записывают m (n – 1) уравнений. При этом контуры выбирают так, чтобы каждый из них содержал хотя бы одну, не учтенную ранее, ветвь;
3) решая систему m уравнений, находят токи. Если значения некоторых токов отрицательные, то действительные направления их будут противоположны первоначально выбранным.
Для электрической цепи рис. 2 n = 2, m = 3, и расчет токов цепи осуществляется путем решения следующей системы уравнений:
![]()
Пример2.Используя метод двух узлов, найти токи в ветвях цепи рисунка 1.29, если E1=20 B, E2=40 B, E3=10 B, E4=50 B, R1=15 Ом, R2=10 Ом, R3=9 Ом, R4=11 Ом, R5=5 Ом.
Построить потенциальную диаграмму для любого замкнутого контура.
Составить баланс мощности.
Решение.Направим токи в ветвях к узлу а и определим напряжение между узлами
Uab=
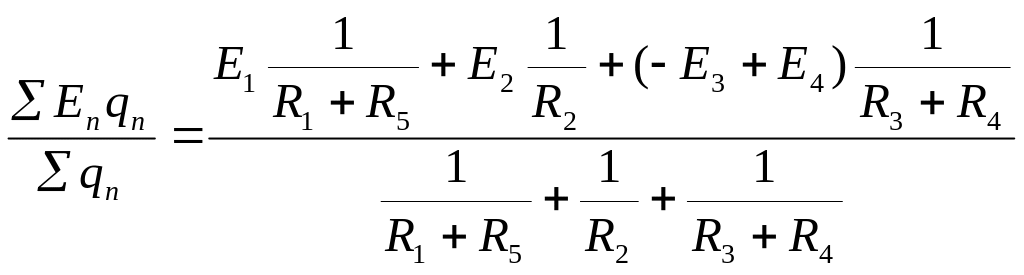 =
35 B
=
35 B
Рисунок 1.29 |
Токи в ветвях рассчитаем по закону Ома:
I=
I1
=
I2
= I3
= |
Положительное направление тока в первой ветви от узла а. Так как направление ЭДС Е1 противоположно направлению тока I1 и ЭДС Е3 противоположно направлению тока I3 ,то источники ЭДС Е1 и Е3 работает в режиме потребителя.
Правильность расчета проверим составлением баланса мощности:
E4I3- E3I3+E2I2-E1I1 = R1I12+ R2I22+ R3I32+ R4I32+ R5I12; 15 = 15 (ВТ)
Потенциальную диаграмму построим для контура acdfbma. Выберем обход контура по часовой стрелке. Обозначим точки, потенциалы которых будем определять, и произвольно примем потенциал одной любой точки равным нулю, например, а=0. Тогда потенциал точки с выше а на величину ЭДС Е3
с = а+Е3 =10В;
d = c + R3I3 = 10+9 0,25 = 12,25 В;
f = d - E4 =12,25-50= -37,75 B;
b =f+R4I3 =-35 B; m= b+E2=5 B; а= mR2I2= 5 10 0,5=0,
что говорит о правильности проведенного расчета.
Д ля
построения потенциальной диаграммы
выбираем масштабы для сопротивления
mR
и
потенциалов
m.
По оси абсцисс откладываем сопротивления
в том порядке, в каком производится
обход контура. По оси ординат откладываем
потенциалы точек (рисунок 1.30).
ля
построения потенциальной диаграммы
выбираем масштабы для сопротивления
mR
и
потенциалов
m.
По оси абсцисс откладываем сопротивления
в том порядке, в каком производится
обход контура. По оси ординат откладываем
потенциалы точек (рисунок 1.30).
Рисунок 1.30
З а д а ч а 2
В четырехпроводную трехфазную сеть с частотой f = 50 Гц включены три однофазных приемника по схеме «звезда» с нулевым проводом ( рис. 2а) и по схеме «треугольнику» (рис.2б). Линейное напряжение сети (Uл), величина и характер приемников даны в табл.2 согласно варианту.
З а д а н и е:
1. Рассчитать сопротивления элементов схемы замещения приемников, используя их параметры из табл.2.
2. Определить фазные и линейные токи каждого приемника (для схемы «звезда» и схемы «треугольник»), и ток в нудевом проводе (для схемы«звезда»)
3. Построить совмещенную векторную диаграмму токов и напряжений (для схемы «звезда» и схемы «треугольник»).
4. Определить активную, реактивную и полную мощность цепи (для схемы «звезда» и схемы «треугольник»).
У к а з а н и я к в ы б о р у в а р и а н т а: вариант определяется по двум последним цифрам номера зачетки.

Таблица 2.
Вари- ант |
Uл (В) |
Приемник zа(zав) |
Приемник zв(zвс) |
Приемник zс (zса) |
||||||
R (Ом) |
L (мГн) |
С (мкФ) |
R (Ом) |
L (мГн) |
С (мкФ) |
R (Ом) |
L (мГн) |
С (мкФ) |
||
1 |
380 |
50 |
- |
- |
- |
- |
40 |
30 |
85 |
60 |
2 |
380 |
55 |
- |
- |
- |
40 |
- |
30 |
- |
60 |
3 |
380 |
- |
50 |
- |
40 |
- |
- |
60 |
60 |
- |
4 |
380 |
- |
50 |
- |
35 |
- |
40 |
70 |
- |
- |
5 |
380 |
45 |
- |
- |
30 |
70 |
- |
- |
- |
80 |
6 |
380 |
50 |
80 |
- |
60 |
- |
- |
- |
- |
70 |
7 |
380 |
- |
- |
75 |
60 |
- |
- |
50 |
50 |
- |
8 |
380 |
50 |
- |
60 |
30 |
- |
- |
- |
80 |
- |
9 |
380 |
- |
70 |
- |
60 |
- |
75 |
50 |
- |
- |
10 |
380 |
45 |
70 |
- |
- |
- |
55 |
- |
75 |
- |
11 |
220 |
45 |
- |
- |
- |
- |
35 |
25 |
80 |
55 |
12 |
220 |
50 |
- |
- |
- |
35 |
- |
25 |
- |
55 |
13 |
220 |
- |
45 |
- |
35 |
- |
- |
55 |
55 |
- |
14 |
220 |
- |
45 |
- |
30 |
- |
35 |
65 |
- |
- |
15 |
220 |
40 |
- |
- |
25 |
65 |
40 |
- |
- |
75 |
16 |
220 |
45 |
75 |
- |
55 |
- |
- |
- |
- |
65 |
17 |
220 |
- |
- |
70 |
55 |
- |
- |
45 |
45 |
- |
18 |
220 |
45 |
- |
55 |
25 |
- |
- |
- |
75 |
- |
19 |
220 |
- |
65 |
- |
55 |
- |
70 |
45 |
- |
- |
20 |
220 |
45 |
60 |
- |
- |
- |
55 |
- |
75 |
- |
21 |
127 |
40 |
- |
- |
- |
- |
30 |
20 |
75 |
55 |
22 |
127 |
45 |
- |
- |
- |
35 |
- |
20 |
- |
50 |
23 |
127 |
- |
40 |
- |
30 |
- |
- |
50 |
50 |
- |
24 |
127 |
- |
40 |
- |
25 |
- |
30 |
60 |
- |
- |
25 |
127 |
35 |
- |
- |
20 |
65 |
50 |
- |
- |
70 |
26 |
127 |
40 |
70 |
- |
50 |
- |
- |
- |
- |
60 |
27 |
127 |
- |
- |
65 |
50 |
- |
- |
40 |
40 |
- |
28 |
127 |
40 |
- |
50 |
20 |
- |
- |
- |
70 |
- |
29 |
127 |
- |
60 |
- |
50 |
- |
65 |
40 |
- |
- |
30 |
127 |
40 |
60 |
- |
- |
- |
50 |
- |
70 |
- |
31 |
660 |
100 |
80 |
30 |
90 |
- |
- |
- |
85 |
- |
Примечание: R L C в фазах включены последовательно.