В в е д е н и е

Задачей расчета рабочего цикла есть определение изме­нения физических параметров рабочего тела на протяжении всего цикла при движении его в объемах конструктивных элементов и систем, которые образовывают двигатель. Расчет ведется по аргументу «время» или «угол поворота ко­ленчатого вала» («угол п.к.в.»), связь между которыми однозначна:

_,

где - шаг угла п.к.в.;

n_д - частота вращения коленчатого вала.

Расхождение в расчетах установившегося и неустано­вившегося режимов будет состоять лишь в том, что для первого достаточно проследить изменение параметров ра­бочего тела на протяжении только одного цикла, а для вто­рого – на всех циклах переходного процесса. Подход к описанию рабочих циклов должный быть единым.

Математическая модель рабочего цикла двигателя должна базироваться на законах, которые описывают ре­альные физические явления, которые протекают в нем, включая общие законы сохранения. Состояние рабочего тела в каждый момент времени и в любой точке объема V, ограниченного конструктивными элементами двигателя, целиком определяется вектором скорости перемещения W, плотностью r, давлением р и температурой Т. Связь между величинами можно установить, воспользовавшись уравне­нием сохранения массы G, импульса ρW, энергии E и уравнением состояния (Менделеева - Клапейрона).

1. Система общих уравнений моделирования физиче­ских явлений в проточных частях двс. Газодинамиче­ские и термодинамические методы моделирования.

Система этих уравнений может быть представлена в ин­тегральной форме Лагранжа [30]:

Уравнение сохранения массы

, (1)

Уравнение сохранения количества движения

, (2)

Уравнение сохранения энергии

, (3)

Уравнение состояния идеального газа

(4)

Или в дифференциальной форме Эйлера:

Уравнение сохранения массы

, (5)

Уравнение сохранения количества движения

(6)

Уравнение сохранения энергии

, (7)

Уравнение состояния идеального газа

(8)

где R_c - суммарный вектор приложенных к объему dV сил;

E - полная энергия, которая состоит из внутренней U и кинетической;

N - мощность внешних сил;

Q - подведенная к объему dV теплота (или отведенная);

F - вектор плотности массовых сил;

D - диссипативная функция;

q_s - вектор потока теплоты, которая проходит через еди­ницу площади в единицу времени;

q - количество теплоты, выделенное единицей массы в единицу времени.

Напомним из курса математики скалярного и векторного поля, что означают дифференциальные операторы:

Векторный оператор – градиент

Скалярный оператор - дивергенция

Поскольку уравнение в дифференциальной форме Эй­лера нашло большее применение, то все дальнейшие изло­жения будут приведены для нее.

Аналитическое решение системы уравнений (5)...(8) не удается найти. Поэтому приходится принимать ряд уп­рощений, благодаря которым можно попробовать найти решение, но уже упрощенной системы.

Обычно принимают следующие упрощения:

1) движение газов в элементах газовоздушного тракта дви­гателя рассматривается одномерным (например, по оси Х);

2) объемные силы отсутствуют (F=0);

3) вязкость газа пренебрежительно маленькая (div=0);

4) в элементах газовоздушного тракта отсутствуют пере­нос теплоты за счет теплопроводности (l=0), а также источ­ника (q=0) и потери теплоты через поверх­ности, которые ограждают рассматриваемый элемент, (q_s=0). Тогда система (5)…(8) примет следующий вид:

Уравнение сохранения массы

, (9)

Уравнение сохранения количества движения

, (10)

Уравнение сохранения энергии

, (11)

Уравнение состояния идеального газа

(12)

Решение такой системы уравнений может быть выпол­нено численными методами с помощью ЭВМ. Математиче­скую модель, основанную на системе уравнений (9)...(12) и успешно применяемую для расчета процессов во всех газо­воздушных трактах ДВС, принято называть газодинамиче­ской [31, 32, 33, 34].

Газодинамическая модель очень слож­на и громоздка в решении даже на ЭВМ. Применяемые для их решения численные методы сеток или конечных разностей требуют выдерживать определенные соотношения между шагом счета по времени Δτ и шагом счета по координате Δх, определяемые критерием Куранта:

В результате при малых шагах по координате получаются очень малые шаги по времени, что сильно увеличивает время расчета. Поэтому иссле­дователи продолжили поиски путей упрощение системы уравнений (9)...(12).

Одни предложили считать, что отклонение скорости течения газа и других параметров от своего среднего значения ничтожно мало. Тогда урав­нение газовой динамики превращаются в уравнения аку­стики [35]:

, (13)

(14)

Здесь а – скорость звука.

Хотя существуют довольно простые методы решения уравнений акустики [35, 36], так называемые «акустиче­ские» методы моделирования процессов в ДВС не нашли широкого применения. Очевидно, это вызвано принятыми предположениями о ничтожном изменении параметров. Та­кие предположения оказались неправомерными для процес­сов в выпускных системах двигателей с газотурбинным наддувом, где амплитуды колебаний давлений достигают 0,1...0,25 МПа. Задание граничных условий тоже связано со значительными трудностями. Поэтому «акустические» ме­тоды применяются в основном лишь для описания колеба­тельных явлений во впускных коллекторах двигателей [36, 37, 38].

Другие предлагают при моделировании процессов в га­зовоздушных объемах двигателя не учитывать изменение параметров состояния газа по координатам и скорость газо­вого потока, то есть считать, что скорость газового потока равняется нулю. Тогда уравнение сохранения массы в инте­гральной форме примет вид:

, (15)

а уравнение закона сохранения количества движения вырож­дается в тождество.

Поскольку при моделировании рабочего цикла двига­теля его газовоздушный тракт разбивается на отдельные элементы (зоны), то массообмен между ними происходит через контрольные поверхности с массовой скоростью rW. При этом считается, что rW в каждой точке этой поверхно­сти одинакова, а число поверхностей (или зон) ограничен­ное. В этом случае уравнения (15) можно переписать в виде:

(16)

где n - число участков, через которые происходит мас­сообмен;

F_i - контрольная поверхность i-го участка;

r_iW_i - массовая скорость потока через поверхность i-го участка.

Величина берется со своим знаком. Если поток втекает в зону, то знак «+», если вытекает из зоны, то знак «-». Урав­нение закона сохранения энергии запишется в виде уравне­ния первого закона термодинамики для равновесных систем с переменной массой:

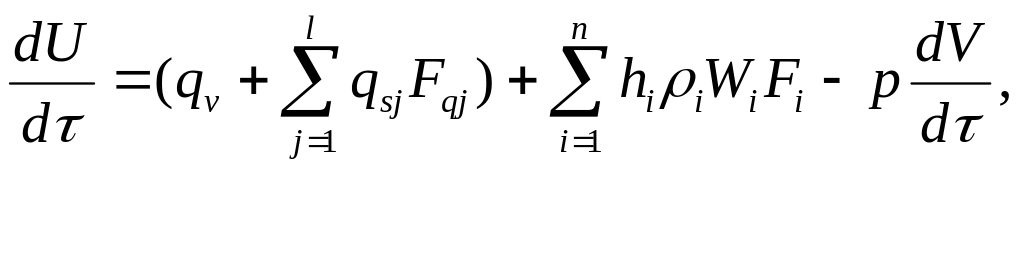(17)

где U - внутренняя энергия газа в рассматриваемой зоне;

q_v - интенсивность объемного источника теплоты в рассматриваемой зоне;

q_s - интенсивность теплообмена через контрольную поверхность;

F_q - площадь контрольной поверхности, через которую происходит теплообмен;

F - площадь контрольной поверхности, которую пе­ресекает поток массы;

l - число участков контрольной поверхности, через которую происходит теплообмен;

n - число участков контрольной поверхности, кото­рую пересекает поток массы;

h – определяемая по заторможенным параметрам удельная энтальпия газа, который пересекает контрольную поверхность.

Чтобы замкнуть систему уравнений (16) и (17) необ­ходимо прибавить уравнение состояния (4). В результате решения этой системы можно определить значения пара­метров состояния газа p, V и T в каждой выделенной зоне газовоздушного тракта двигателя в данный момент (или по углу п.к.в.). Методы, основанные на описании процессов в газовоздушных полостях двигателей с помощью системы уравнений (16), (17) и (4) получили название термо­динамических. Многолетний опыт расчетов показал, что он хорошо работает при относительно низких скоростях га­зовых потоков и небольшой длине расчетных зон [2, 39...53]. Контроль длины расчетной зоны, которая обеспе­чивает пригодную для практических целей точность, сле­дует вести по величине числа Струхаля [2]. Как показано в работах [2, 48], достаточная точность расчетов обеспечива­ется при

Расчетная схема газовоздушного тракта двигателя, раз­работанная на кафедре «Теплотехника и тепловые двига­тели» УкрГАЖТ приведена на рис. 1. Она может изменяться в зависимости от целей исследования. Выделе­ние расчетных зон производится путем распределения га­зовоздушного тракта на элементы определенного назначе­ния: воздушный фильтр, трубопровод от фильтра к нагнета­телю, нагнетатель, охладитель наддувочного воздуха, над­дувочный коллектор от компрессора до охладителя, впускной коллектор от охладителя до впускных клапанов, цилиндр, выпускные коллекторы, преобразователь импульсов (если он есть), турбина, глушитель.

В общем случае моделирование процессов в любой из расчетных зон может проводиться разными методами: газодинамическими, акустическими и термодинамиче­скими. Тогда для каждой расчетной зоны складывается своя система уравнений для определения параметров газа в ней. Но стыковка зон вырабатывается из условия равенства по­токов массы и энергии через поверхности разделения зон.

Применение разных методов моделирования процессов в разных зонах, как правило, приводит к значительному ус­ложнению всего расчета, так как в рамках полной модели двигателя приходится использовать разные методы и алго­ритмы расчета для отдельных зон. Применение же единого метода упрощает расчетную схему и сокращает время рас­чета.

Таким единым методом представляется термодинамиче­ский подход. Последнее относится только к моделированию процес­сов в газовоздушных полостях ДВС. Моделирование же движения коленчатого вала двигателя, ротора турбоком­прессора, работы регулятора, системы дистанционного управления должно применяться с учетом законов меха­ники и законов тех явлений, которые протекают в этих сис­темах.

Именно такой принцип построения объединенной мо­дели двигателя был использован в работах [47, 49], что раз­решило с одинаковой точностью и информативностью мо­делировать рабочие процессы комбинированных ДВС как на установившихся, так и на переходных режимах.

Р ис.1 Расчетная схема газовоздушного тракта двига­теля