13. Распределение межпоездных интервалов в вероятн. Графике движ.

Нагрузка на ЭС в осн. определ-ся числом поездов в расчет. фидерн. зоне. Методика расчета системы ЭС рассматр. число поездов, как сл. величину, причем распред. подчиняется биномиальн. закону:

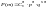m-поезд.; n-нитей гр-ка. (p*q = для 1поезда.)

Сист. анализ показал, что по этому распр-ю можно получить ф-ю распред. межпоезд. интервалов.

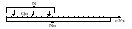
N-число уч-ков , N- число уч-ков с поездами

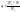
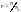
прим. допущ. , что 1 из блок-участков занят поездом, тогда вероятность , что рядом с ним по крайней мере m-1 инт. будет своб., т.е межпоездн. интервал будет 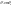, тогда ф-я распред:

14. Непрерыв. Ф-ция распределения межпоездн. Интервалов.

Изв. 5 типов поездов: N1->V1, N2->V2 …N5->V5 тип поезда опр. его скорость; допустим, изв. очередность 12135, нужно рассчитать каждую пару поездов и миним. инт. между ними V1-V2->Q1 и.т.д.

2-1,1-3,3-5. Реальн. м/п интервал может отлич. от мин. и равен: 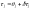, где Qj-миним. м/п интервал, явл. определенной велич. ; дTj-случ. приращение м/п интервала. Нужно создать алгоритм приращения м/п интервала. Возьмем сумму инт. за сутки:

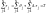Т-суточный врем. интервал

Определим резерв времени, образ. при пропуске поездов с мин. м/п интерв. 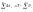Если этот резерв разбить поровну для кажд. пары поездов, то получим среднее приращение м/п интервала.

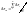Примем по аналогии с дискрет. ф-цией распредел-я вероятностей приращения м/п интервала в виде экспоненты:

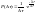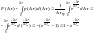проинтегрир. данное выр-е для нахожд. ф-ции распр-я приращения м/п инт. ф-ция распр. м/п интервала может прин. случайные знач. , поэтому приравн. к сл. числу ψ :

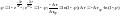
15. Алгоритм работы имитационной модели

Слово произошло от имени лат. матем. (algorithmi)

Алгоритм (Колмогоров)- всякая система вычислений, выполняемых по строго опред. правила, которые посредством опр. числа шагов приводят к решению поставленной задачи

Алгоритм(Марков) – точное предписание, определ. вычислительный процесс опред. искомый результат.

16. Свойства алгоритма

Дискретность – решение задач посредств. выполнения простых шагов.

Каждое след. действие алгоритма вып. после выполнения предыдущего.

Определенность –

Результативность –

Массовость – алгоритм разраб. некоторого класса задач с разными исх. данными.

17. Виды алгоритмов

1.Прикладной – для решения прикладных задач

2.Рекурсивный – вызывает сам себя, пока не будет достигнуто опр. условие

3.Параллельные – для вычислит. машин, способных выполнять несколько алгоритмов одновременно

4.Механический – жесткий детерминиров. , алгоритм раб. машины

5.Вероятностный – дает программу решения задачи несколькими способами, привод. к вероятному достижению результата.

6. Эвристический – в котором достижение конечного рез-та программы действия однозначн. не определено, так же в нем не обозначена вся последов-ть действий(пример – инструкции)

7. Линейный – набор команд, вып. последов-но друг за другом

8. Разветвляющийся – содержит хотя бы одно условие

9. Циклический – многократное повторение 1 и тех же действий, но с новыми исх. данными.