Постоянное магнитное поле в вакууме Задача 1

По круговому витку радиуса r=0,1 м циркулирует ток силы I=1 А. Найдите магнитную индукцию В: а) в центре витка; б) на оси витка на расстоянии b=0,1 м от его центра. [а) 6,3 мкТл; б) 2,2 мкТл]

Указания по решению.

1)Если ток протекает по линейному проводнику формы L, то индукция магнитного поля в произвольной точке находится через криволинейный интеграл:

,

где радиус-вектор направлен от элемента тока в рассматриваемую точку поля.

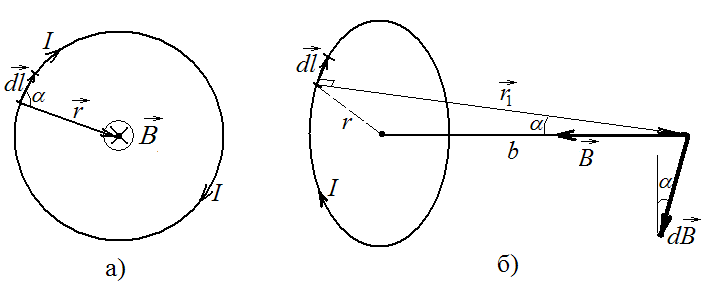
а) Магнитная индукция элементарного поля в центре витка по закону Био-Савара-Лапласа равна

,

т.е. вектор перпендикулярен плоскости рисунка и численно равен

.

Учитывая, что все элементы тока на круговом витке одинаково расположены по отношению к центру витка, получим

.

б) Магнитная индукция элементарного поля на оси витка по закону Био-Савара-Лапласа равна

.

Отсюда ясно (по определению векторного произведения), что вектор перпендикулярен плоскости, образованной векторами и , т.е. для каждого элемента тока вдоль витка имеет свое направление. Совокупность векторов образует коническую поверхность, ось которой совпадает с осью витка (рис. 6 б)). Векторная сумма всех с учетом симметрии будет направлена по оси витка и численно равна сумме проекций отдельных на эту ось:

.

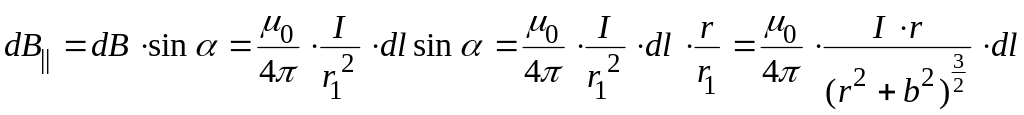Учитывая, что все элементы тока на круговом витке равноценно расположены по отношению к центру витка, получим

.

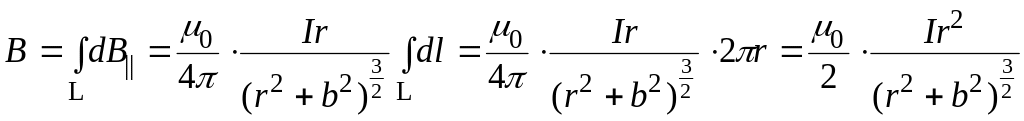Задача 2

Бесконечно длинный прямой проводник, по которому течет ток силой I=5 A, согнут под прямым углом (рис. 8). Найти индукцию магнитного поля на расстоянии a = 10 см от вершины угла в точках A и C, лежащих соответ­ственно на биссектрисе прямого угла и на продолжении од­ной из сторон. [240 мТл; 5 мкТл]

Указания по решению.

В любой точке индукция магнитного поля мо­жет быть найдена как векторная сумма индукций полей, созданных токами, протекающими по двум частям 1 и 2 провода:

.

С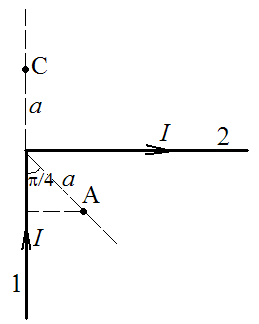 огласно условию, проводник бесконечно длинный, что позволяет не учитывать магнитное поле, создаваемое тока­ми в подводящих проводах, идущих к источнику.

Модуль индукции магнитного поля в любой точке, созда­ваемого каждым из проводников, может быть найден по формуле поля прямого тока конечной длины (см. задачу 1.2 ):

.

В точке A, как следует из закона Био-Савара-Лапласа, векторы и направлены одинаково и перпендикулярны плоскости рисунка. Следовательно,

,

В точке C проводник 1 поля не создает, так как для любо­го элемента этого проводника =0. Поэтому

.

Вследствие симметричного расположения точки A относительно частей проводника , поэтому

. (4)

Из рис. видно, что для поля проводника 1 в точке A

.

Тогда

(Тл).

Для точки C

, .

Тогда

(Тл).

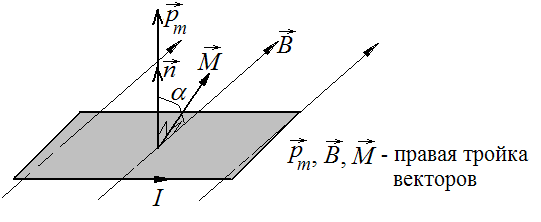
Задача 3

В ОМП с индукцией В=0,1 Тл помещена квадратная рамка площадью S=25 см². Нормаль к плоскости рамки составляет с направлением магнитного поля угол  =60⁰. Определите: 1) вращающий момент , действующий на рамку; 2) магнитный момент рамки. По рамке течет ток I=1 А. [217 мкНм; 2,5 мАм²]

Указания по решению. Изобразим на рисунке плоскость рамки, укажем направление тока в ней и соответственно этому направлению изобразим положительную нормаль .

Магнитный момент рамки будет направлен так же как и нормаль и равен

.

Вращающий момент есть вектор, направленный перпендикулярно векторам и , численно равный

.

Самостоятельно произведите вычисления и сравните ответ.