Комбинированные задачи

1. 

   

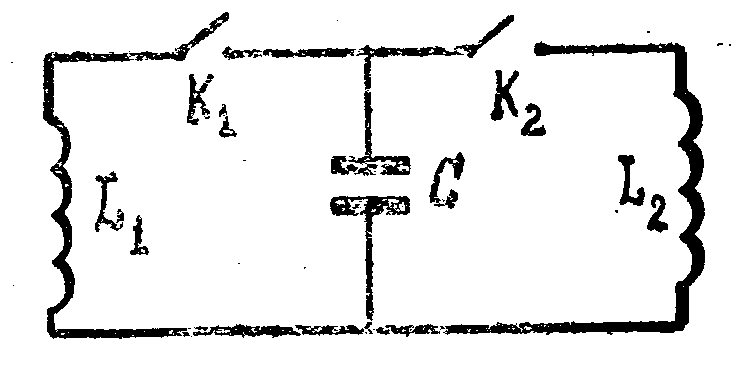
   Две катушки самоиндукции с индуктивностями L₁ и L₂ подключены через ключи K₁ и K₂ к конденсатору с емкостью С. В начальный момент времени оба ключа разомкнуты, а конденсатор заряжен до разности потенциалов V. Сначала замыкают ключ К₁ и, когда напряжение на конденсаторе станет равным нулю, замыкают ключ К₂. Определить максимальное и минимальное значения тока, протекающего через катушку L₁ после замыкания ключа K₂- Активным сопротивлением катушек пренебречь.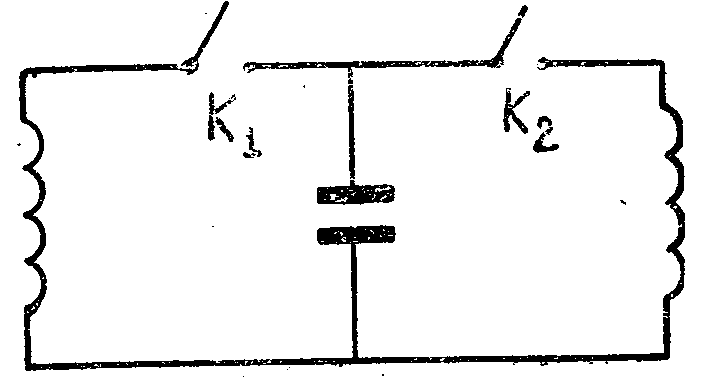

2. Две одинаковые катушки самоиндукции подключены через ключи K₁ и К₂ к конденсатору. В начальный момент времени оба ключа разомкнуты, а конденсатор заряжен до разности потенциалов V. Сначала замыкают ключ Ê₁ и, когда напряжение на конденсаторе станет равным нулю, замыкает ключ К₂. Определить максимальное напряжение на конденсаторе после замыкания ключа K₂. Активным сопротивлением катушек пренебречь.

1. 

   По вертикальным проводящим рельсам в поле тяжести может скользить без трения контакт массой m и длиной l. Рельсы замкнуты на идеальную индуктивность L и находятся в горизонтальном магнитном поле с индукцией В перпендикулярной плоскости рисунка. В начале контакт поддерживался внешней силой в покое. Определить максимальное смещение контакта от начального положения, если внешнюю силу убрать, так что контакт начинает движение вниз с нулевой начальной скоростью.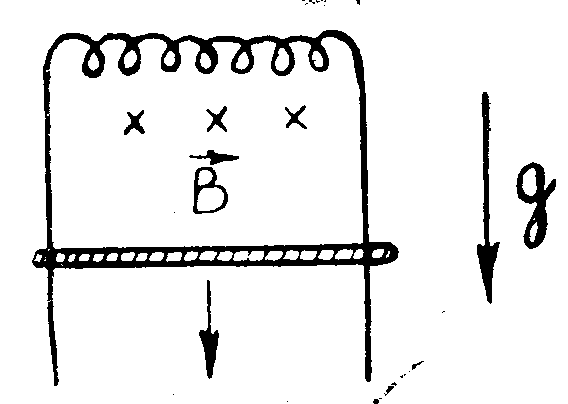

1. 

   По вертикальным проводящим рельсам в поле тяжести может скользить без трения контакт массой m длины l. Рельсы замкнуты на идеальную индуктивность L и находятся в горизонтальном магнитном поле, перпендикулярном плоскости рисунка. Вначале контакт поддерживался внешней силой в покое. В некоторый момент времени внешняя сила убирается и контакт начинает движение вниз с нулевой начальной скоростью. Определить величину индукции магнитного поля В, если известно, что максимальная скорость, с которой движется контакт, равна V₀.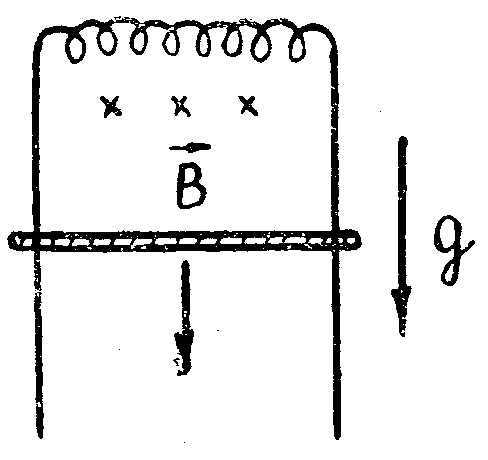

Колебания

1. 

   Колебательный контур, состоящий из катушки индуктивности н емкости, через ключ К подключен к источнику постоянной ЭДС с внутренним сопротивлением R. Первоначально ключ К замкнут. После установления стационарного режима ключ размыкают, и в контуре возникают колебания с периодом Т. При этом амплитуда напряжения на конденсаторе в п раз больше ЭДС батареи. Найти индуктивность катушки и емкость конденсатора. Омическим сопротивлением катушки пренебречь.

1. 

   Колебательный контур, состоящий из катушки с индуктивностью L, емкости С и идеального диода D, через ключ К подключают к источнику постоянной ЭДС, равной Е, на время , а затем отключают. Найти зависимость напряжения на конденсаторе С от времени после размыкания ключа К. Нарисовать график этой зависимости. Внутренним сопротивлением источника и омическим сопротивлением катушки пренебречь.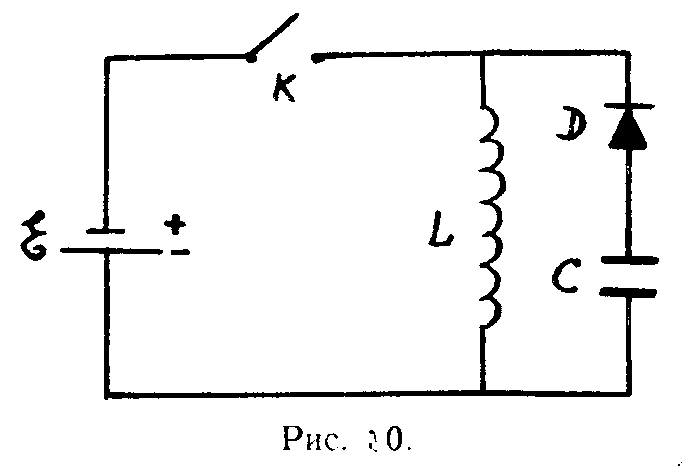

2. В колебательном LCR — контуре сопротивление невелико, так что колебания в нем затухают слабо. Для получения незатухающих колебаний поступают следующим образом: дважды за период в моменты, когда ток в цепи максимален, катушку индуктивности быстро растягивают от длины l₁ до длины l₂, а в моменты, когда ток минимален, ее быстро сжимают до прежнего размера (параметрический резонанс). При каком относительном изменении длины катушки l/l колебания в контуре не будут затухать? Индуктивность катушки считать обратно .пропорциональной ее длине.

1. 

   В последовательном колебательном LCR — контуре сопротивление невелико, так что колебания в нем затухают слабо. Для получения незатухающих колебаний поступают следующим образом: дважды за период в моменты, когда заряд конденсатора максимален, его пластины быстро раздвигают от расстояния d₁, до расстояния d₂, а в моменты, когда заряд равен нулю, их быстро сдвигают до прежнего расстояния (параметрический резонанс). При каком относительном изменении расстояния между обкладками d/d колебания в контуре не будут затухать?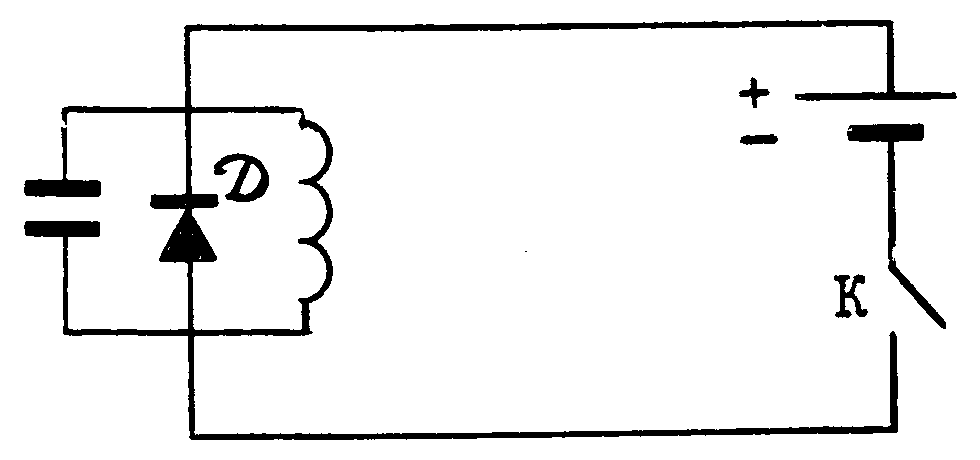

2. В схеме, изображенной на рисунке (D — идеальный диод), ключ К замыкают на время , а затем размыкают. Сила тока в катушке индуктивности в момент размыкания I₀. Через сколько времени после размыкания ток в катушке I_L достигнет максимального значения, если оно равно 2I₀? Построить график I_L(t) (0 < t< T).

1. 

   В схеме в начальный момент времени ключи K₁ и K₂ разомкнуты, а конденсатор С не заряжен. Сначала замыкают ключ К₁. В момент, когда напряжение на конденсаторе оказывается равным сумме ЭДС батарей 1₁ и 1₂, замыкают ключ K₂. Определить через какое время после замыкания ключа К₂ величина силы тока через катушку индуктивности L увеличится в 3 раза. Заданными считать L, С и отношение 1₂/1₁ = 0,8. Всеми омическими потерями пренебречь.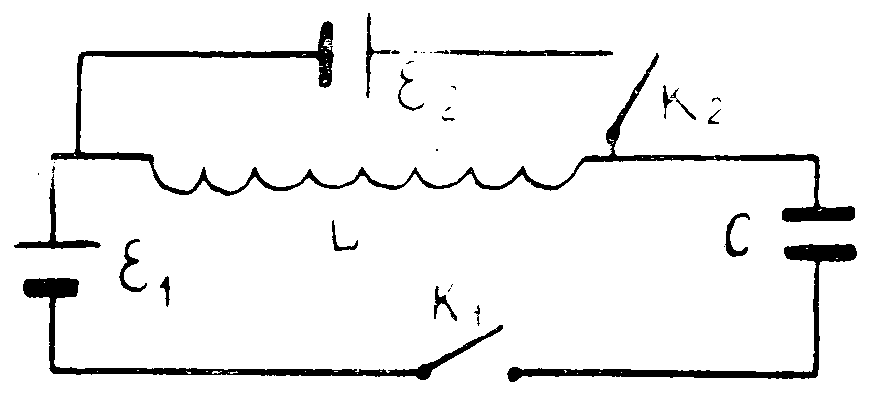

1. 

   В схеме, изображенной на рисунке, в начальный момент времени ключи К₁ и K₂ разомкнуты, а конденсатор С не заряжен. Сначала замыкают ключ К₁. В момент когда напряжение на конденсаторе оказывается равным ЭДС. батареи 1₂, замыкают ключ K₂. Считая известными С, L и отношение 1₂/1₁ = 1,8, определить через какое время после замыкания ключа К₂ величина силы тока через катушку индуктивности L увеличится в 2 раза. Всеми омическими потерями пренебречь.

1. 

   В схеме в начальный момент времени ключи К₁ и К₂ разомкнуты, а конденсатор С не заряжен. Сначала замыкают ключ K₁. В момент, когда напряжение на конденсаторе оказывается равным разности ЭДС батарей 1₁ и 1₂, замыкают ключ K₂. Через время  после замыкания ключа К₂ величина силы тока через катушку индуктивности L увеличивается в 3 раза. Считая известными время  и отношение 1₂/1₁ = 0,6, определить период собственных колебаний колебательного контура, состоящего из индуктивности L и емкости С. Всеми омическими потерями пренебречь.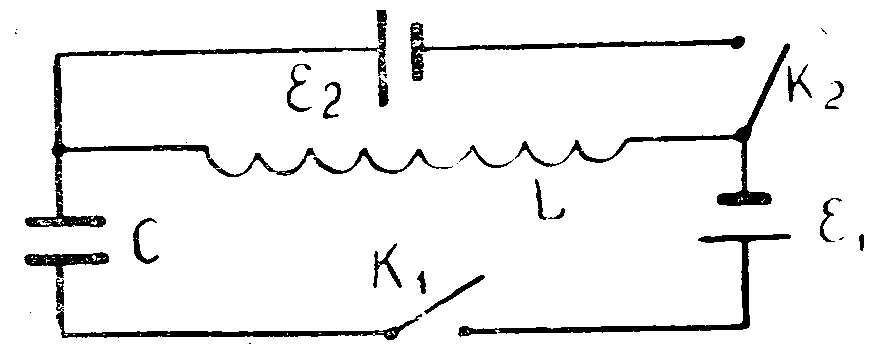

1. 

   В схеме, изображенной на рисунке, в начальный момент времени ключи K₁ и K₂ разомкнуты, а конденсатор С не заряжен. Сначала замыкают ключ K₁. В момент, когда напряжение на конденсаторе оказывается равным ЭДС. батареи 1₂, замыкают ключ K₂. Через время  после замыкания ключа К₂ величина силы тока через катушку индуктивности L увеличилась в 4 раза. Считая известными время  и отношение 1₂/1₁ = 0,4, определить период собственных колебаний колебательного контура, состоящего из индуктивности L и емкости С. Всеми омическими потерями пренебречь.

1. 

   В цепи, изображённой на рисунке, при разомкнутом ключе К заряд на конденсаторе с ёмкостью C₁ (C₁ = C₂/3) равен q₁, а конденсатор с емкостью С₂ не заряжен. Через какое время после замыкания ключа заряд на конденсаторе С₂ будет иметь максимальное значение? Чему будет равен этот заряд? Омическими потерями в катушке с индуктивностью L пренебречь.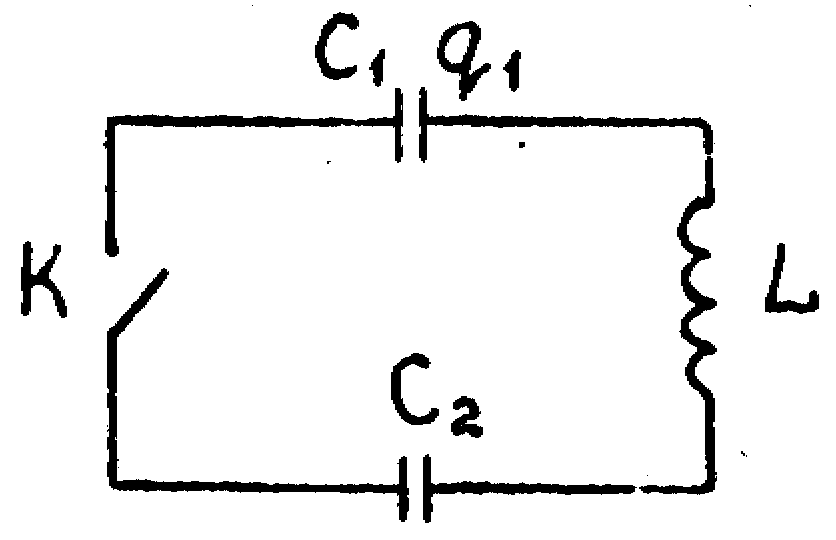

1. По вертикальным проводящим рельсам в поле тяжести может скользить без трения контакт массой m и длиной l. Рельсы замкнуты на идеальную индуктивность L и находятся в горизонтальном магнитном поле с индукцией В перпендикулярной плоскости рисунка. В начале контакт поддерживался внешней силой в покое. Определить максимальное смещение контакта от начального положения, если внешнюю силу убрать, так что контакт начинает движение вниз с нулевой начальной скоростью.

1. По вертикальным проводящим рельсам в поле тяжести может скользить без трения контакт массой m длины l. Рельсы замкнуты на идеальную индуктивность L и находятся в горизонтальном магнитном поле, перпендикулярном плоскости рисунка. Вначале контакт поддерживался внешней силой в покое. В некоторый момент времени внешняя сила убирается и контакт начинает движение вниз с нулевой начальной скоростью. Определить величину индукции магнитного поля В, если известно, что максимальная скорость, с которой движется контакт, равна V₀.

1. В 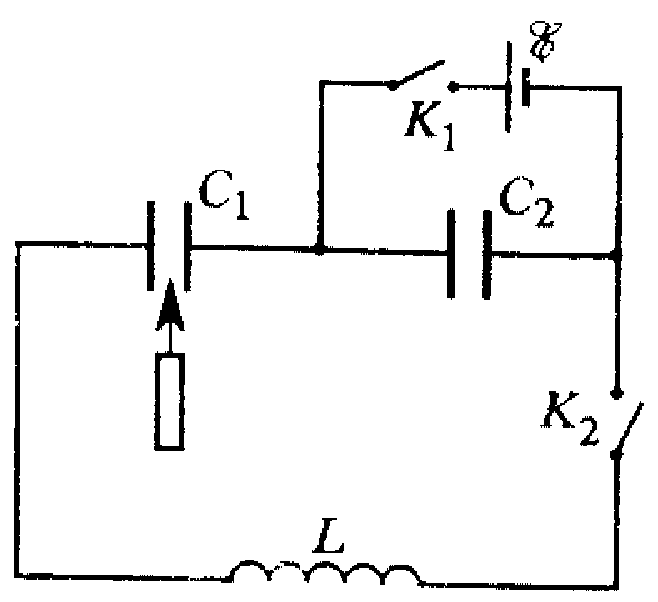схеме, изображенной на рисунке, сначала замыкают ключ К₁ и после того, как конденсатор емкостью С₂ полностью зарядится от батареи с ЭДС 1, ключ К₁ размыкают и замыкают ключ К₂. После замыкания ключа К₂ в схеме происходят свободные незатухающие колебания. Когда напряжение на конденсаторе емкостью С₁ достигает максимального значения, в него быстро (за время, малое по сравнению с периодом колебаний) вставляют диэлектрическую пластину, что приводит к увеличению его емкости  раз.

1. Чему равен начальный ток в цепи после замыкания ключа К₂?

2. Определить максимальный ток в цепи после вставки пластины.

1. В 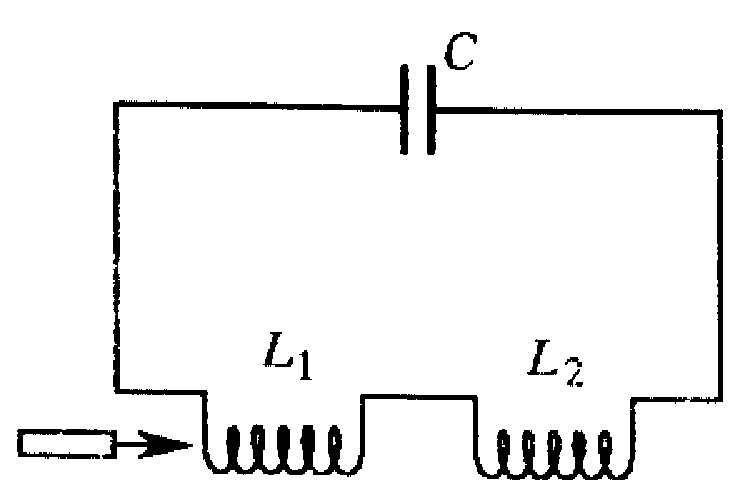колебательном контуре, состоящем из двух последовательно соединенных катушек с индуктивностями L₁ и L₂ и конденсатора емкостью C, происходят свободные незатухающие колебания, при которых амплитуда колебаний тока равна I₀. Когда сила тока в катушке L₁ максимальна, в нее быстро (за время, малое по сравнению с периодом колебаний) вставляют сердечник, что приводит к увеличению ее индуктивности в  раз.

1. Определить максимальное напряжение на конденсаторе до вставки сердечника.

2. Определить максимальное напряжение на конденсаторе после вставки сердечника.

1. В колебательном контуре, состоящем из двух параллельно соединенных конденсаторов с емкостями C₁ и С₂ и катушки с индуктивностью L, происходят свободные незатухающие колебания, при которых амплитуда колебаний заряда на конденсаторе С₂ равна q₀. В конденсаторе C₁ расположена диэлектрическая пластина с диэлектрической проницаемостью , которая полностью заполняет его пространство. Когда заряд на конденсаторе С₁ достигает максимального значения, пластину быстро (за время, малое по сравнению с периодом колебаний) удаляют из конденсатора,

1. Определить новый период колебаний.

2. Определить амплитуду новых колебаний тока в катушке.

1. В 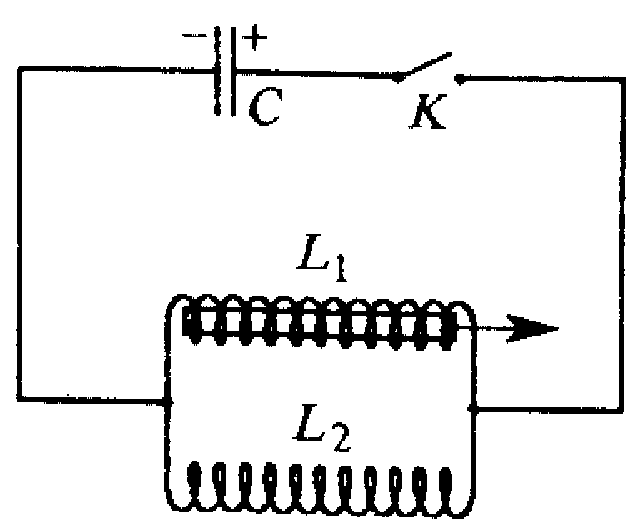схеме на рисунке конденсатор емкостью С заряжен до некоторого напряжения. После замыкания ключа К в схеме происходят свободные, практически незатухающие колебания, при которых амплитудное значение тока в катушке с индуктивностью L₂ равно I₀. Когда ток в катушке с индуктивностью L₁ достигает максимального значения, из нес быстро (за время, малое по сравнению с периодом колебаний) выдвигают сердечник, что приводит к уменьшению ее индуктивности в  раз.

1. Найти ток через катушку L₂ сразу после замыкания ключа.

2. Найти максимальное напряжение на конденсаторе после выдвигания сердечника.