Применение методов математической статистики при разработке управленческих решений
Одна из основных целей теории измерений - борьба с субъективизмом исследователя. И в этом случае, математическая статистика – основа получения статистически обоснованых заключений и выводов, необходимых при принятии решений.
Математические методы являются основным инструментом принятия решений в операционном менеджменте. Их используют преимущественно при принятии решений в условиях определенности. Они требуют специальной математической подготовки. Кроме того, обычно требуется адаптация методов к конкретным условиям, в связи с чем менеджеры редко сами производят расчеты, а обращаются к специалистам университетов или консалтинговых фирм
Применение методов мат.статистики позволяет решать как минимум 3 задачи: 1) описание данных, 2) оценивание данных и 3) проверка гипотез.
При этом необходимо помнить, что каждая организация самостоятельно определяет: какие статистические данные ей необходимо аккумулировать и в каком виде. Все данные можно сгруппировать по 3 основным шкалам измерения: номинальная, порядковая, метрическая.
Знание основных шкал измерения необходимо для правильного выбора метода исследования, т.к. одну и ту же величину (например, заработную плату) в зависимости от шкалы измерения (метрическая: 5 ты.руб., 15 тыс.руб. или интервальная до 5 ты.руб., 10-15 тыс.руб.) расчет необходимо вести по разным формулам средней (простая среднеарифметическая и среднеарифметическая для интервального ряда)
Основные характеристики трех шкал измерения
Шкала |
Примеры |
Процедуры измерения |
Разрешенные математические операции |
Номинальная (теснота связи – лямда) |
Пол, раса, семейное положение т.е. А≠В≠С |
Классификация по категориям |
Никаких мат. операций делать нельзя, кроме подсчета кол-ва каждой категории переменной и сравнения размеров категорий |
Порядковая (теснота связи – коэф-т корреляции Спирмена) |
Социально-экономический статус, отношение и мнение т.е. А‹В‹С, но на сколько – не знаем |
Классификация по категориям, а также ранжирование категорий |
Подсчет кол-ва каждой категории переменной, сравнение размеров категорий, а также суждения типа «более чем» и «менее чем» |
Метрическая/ интервальная (у них есть фиксированное начало отсчета и равные интервалы) (коэф-т корреляции Пирсона) |
Возраст, кол-во детей, доход (от … до …) т.е. А‹В‹С и знаем на сколько (в соц. практике очень мало) |
описание различий между значениями на основе равных единиц |
другие математические операции (сложение, вычитание, умножение, деление, извлечение квадратного корня и т.д.) |
Анализ временных рядов
В случае, если мы исследуем (в т.ч. и во времени) статистическую совокупность по какому-либо одному признаку (возраст, рождаемость, заработная плата, успеваемость) со всеми его статистическими характеристики (минимум, максимум и среднее значение и т.п.), то методы анализа такого рода называются одномерными или анализом временных рядов.
В случае, когда мы проводим анализ связи между двумя и более переменными, то такой анализ называют много мерный или ассоциативным анализом.
К самым простым методам анализа временных рядов в данном случае относят:
Количественный подсчет, сравнение (в том числе и в %) и группировки
Расчет темпов роста и прироста. (темп прироста, характеризует относительную скорость изменения уровня ряда в единицу времени. Физически темп прироста показывает, на какую долю (или процент) уровень данного периода или момента времени больше (или меньше) по сравнению с предыдущим. Другими словами темп прироста отвечает на вопрос «на сколько процентов подорожал товар». Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит темп роста, показывающий, во сколько раз в среднем за единицу времени изменился уровень исследуемого ряда)
Метод экстраполяции (предполагает, что тенденции прошлого продлеваются на будущее состояние развития объекта исследования. Перенос тенденций из прошлого в будущее может проводиться различными методами, но самые простые основываются на средних величинах).
Роль и виды средних величин
Средние величины достаточно часто используются при разработке управленческого решения, т.к. средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Достоинство средних величин заключается в том, что они заменяют индивидуальные значения исследуемого процесса (х1, х2, х3, … где х – например, заработная плата отдельно взятого работника организации) некоторой уравновешенной средней величиной Х – уровнем средней заработной платой в организации.Средние величины исчисляются для характеристики уровня цен, заработной платы, основного капитала, численности населения и др. однородной совокупности социально-экономических явлений.
Важнейшими условиями (принципами) для правильного вычисления и использования средних величин является следующие:
В каждом конкретном случае необходимо исходить из качественного содержания осредняемого исследуемого процесса, учитывать взаимосвязь изучаемых признаков и имеющиеся для расчета данные.
Индивидуальные значения, из которых вычисляются средние, должны относиться к однородной совокупности, а число их должно быть значительным
Совокупность (статистический ряд) – статистические данные, собранные по какому-либо признаку
Признак – конкретный показатель (заработная плата, возраст, уровень образования, пол и т.п.)
Частота показывает сколько раз данный признак (заработная плата, возраст, уровень образования, пол и т.п.) встречается в исследуемой совокупности
Простая среднеарифметическая величина представляет собой среднее слагаемое, при определении которого общий объем исследуемого признака (например, заработная плата) в общей совокупности данных поровну распределяется между всеми единицами, входящими в данную совокупность (например, средняя заработная плата 1 сотрудника за год, средняя заработная плата работников предприятия за 1 месяц).
В случае, когда варианты исследуемой совокупности (Х – заработная плата) встречаются неодинаковое количество раз (F – число рабочих) – расчет средней величины осуществляется по формуле среднеарифметической взвешенной.
Например, необходимо найти среднюю заработную плату рабочих цеха за месяц
Заработная плата одного рабочего тыс.руб. (X) |
Число рабочих (F) |
3,2 |
20 |
3,3 |
35 |
3,4 |
14 |
4,0 |
6 |
В этом случае, средняя заработная плата может быть получена путем деления общей суммы заработной платы на общее число рабочих:
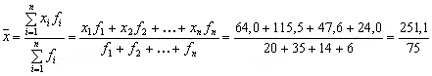
В случае, если значения признака находятся не в абсолютных величинах (5 тыс. руб., 25 тыс. руб., 30,8 тыс. руб.), а имеют интервальные границы (заработная плата от 10 до 15 тыс. руб. и т.п.), то расчет средней должен осуществляться по формулам средней арифметической для интервального ряда.
Например, необходимо найти среднюю заработную плату рабочих цеха за месяц
Заработная плата одного рабочего тыс.руб. (X) |
Число рабочих (F) |
Среднее значение интервала (Х’) |
Произведение середины интервала (з/пл) на число рабочих (Х’х F) |
до 20 |
5 |
(18 + 20) / 2 =19 18 в данном случае граница нижнего интервала. Вычисляется как 20 — (22-20) |
235 |
20 — 22 |
25 |
(20 + 22) / 2 = 21 |
625 |
22 — 26 |
190 |
(22 + 26) / 2 = 24 |
4560 |
26 — 30 |
80 |
(26 + 30) / 2 = 28 |
2240 |
30 и более |
40 |
(30 + 34) / 2 = 32 |
1280 |
Итого |
500 |
|
11940 |
При этом необходимо помнить, что при расчете средней арифметической для интервального ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда. В случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.
Средние, вычисляемые из интервальных рядов являются приближенными.
В тех случаях когда известны индивидуальные значения признака (Х – средняя заработная плата одного рабочего) и произведение Х*F, а частоты (F – количество рабочих) неизвестны - используется средняя гармоническая.
Например, необходимо найти среднюю заработную плату рабочих за 1 месяц по трем предприятиям
Предприятие |
Средняя заработная плата одного рабочего тыс.руб. (X) |
Фонд оплаты труда сотрудников предприятия за 1 месяц |
1 |
18,2 |
3640 |
2 |
20,4 |
3060 |
3 |
23,5 |
2350 |
Итого |
|
9050 |
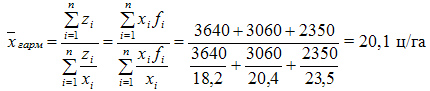
Средняя экспоненциальная, позволяет учитывать «возраст» данных постоянно адаптируясь к данным за счет новых значений. Другими словами, чем «старше» наблюдение, тем меньше оно должно оказывать влияние на величину скользящей средней. То есть влияние прошлых наблюдений должно затухать по мере удаления от момента, для которого рассчитывается средняя.
Роль описательных статистик
Мода показывает наиболее часто встречающееся значение признака в совокупности (чаще всего студенты получают на экзаменах оценку «4», или чаще всего сотрудники получают заработную плату в размере 12 ты.руб.)
Медиана показывает середину ряда, т.е. 50% (половина сотрудников на предприятии получает заработную плату не более 15тыс.руб. Не более, т.к. сюда входит вся заработная плата, получаемая работниками до 15 тыс. руб.: и 5 тыс.руб., и 7тыс.руб., и 9 тыс.руб., и 15 тыс.руб.)
Мin – указывает минимальное значение
Max – указывает максимальное значение
Дисперсия -