Вопросы для самоконтроля

1. Дайте определение случайной величины.

2. Приведите примеры случайных величин.

3. Как задаются случайные величины?

4. Что такое закон распределения случайной величины?

5. Что такое функция распределения случайной величины?

6. Что такое плотность вероятности случайной величины?

7. Каковы свойства функции распределения?

8. Каковы свойства плотности вероятности?

9. Как определить вероятность попадания случайной величины в интервал?

10. Каковы типовые законы распределения случайных величин?

Тема №7

Числовые характеристики случайных величин

Теоретическое введение.

Характеристиками положения случайной величины являются математическое ожидание, мода и медиана.

Средним значением, или математическим ожиданием случайной величины называют сумму

(для дискретной случайной величины),

или интеграл

(для непрерывной случайной величины),

причем предполагается, что ряд и интеграл сходятся абсолютно. В этих формулах - значения случайной величины, их вероятности, - плотность вероятности.

Свойства математического ожидания:

1) , где С - const;

2) ;

3) , где и - любые случайные величины;

4) , если и - независимые случайные величины.

Случайные величины и называются независимыми, если для любых x и y имеет место равенство

.

Модой ( ) дискретной случайной величины называется ее наиболее вероятное значение. Модой непрерывной случайной величины называется то ее значение, при котором плотность вероятности максимальна.

Медианой непрерывной случайной величины называется такое ее значение , для которого

.

Начальные и центральные моменты k-го порядка случайной величины определяются соответственно формулами:

и

Второй центральный момент называется дисперсией случайной величины :

(для любой дискретной случайной величины) и

- (для непрерывной случайной величины).

Для вычислений дисперсии удобна следующая формула:

Свойства дисперсии:

1) , где C-const;

2) ;

3) Если и - независимые случайные величины, то .

Центральные моменты выражаются через начальные моменты по следующим формулам:

Центральный момент второго порядка характеризует рассеяние случайной величины.

Асимметрия случайной величины определяется как отношение

где - среднее квадратическое отклонение случайной величины . Если распределение симметрично относительно математического ожидания, то . Если , то кривая плотности вероятности имеет "скос" с левой стороны; если , то с правой стороны.

Эксцессом случайной величины называется величина

.

Для нормального закона распределения . Величина характеризует крутизну кривой плотности вероятности по сравнению с кривой Гаусса (нормальным законом). Для островершинных кривых , для пологих .

Заметим, что размерность величин и совпадает с размерностью самой случайной величины , а размерность равна квадрату размерности .

Примеры и задачи.

Пример 1. Число -частиц, достигающих счетчика в некотором опыте, является случайной величиной , распределенной по следующему закону:

Найти : а) математическое ожидание и дисперсию числа частиц, достигающих счетчика; б) вероятность того, что число частиц, достигших счетчика, не меньше 4; в) дисперсию случайной величины

Решение. Зададим матрицу

> R:=matrix([[xi, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], [p, .21e-1, .81e-1, .156, .201, .195, .151, .97e-1, .54e-1, .26e-1, .11e-1, .7e-2]]);

а) Вычислим математическое ожидание

> nu[1]:=sum(R[1,i]*R[2,i], i=2..11);

б) Найдем вероятность того, что число частиц, достигших счетчика, не меньше 4

> P(xi>=4):=sum(R[2,i], i=6..11);

в) Найдем дисперсию

> mu[2]:=sum((R[1,i]-nu[1])^2*R[2,i], i=2..11);

Задача 1. Случайная величина имеет биномиальное распределение:

,

где m=0, 1, ..., n.

Найти и .

Пример 2. При 10000 бросаниях монеты "герб" выпал 5400 раз. Следует ли считать, что монета несимметрична?

Решение. Напомним правило "трех сигм" в схеме Бернулли. Из интегральной теоремы Муавра-Лапласа следует, что вероятность того, что случайная величина попадет в интервал , где _, равна

=0.9973.

Другими словами, факт попадания практически достоверен. Эта формула называется правилом "трех сигм". Она указывает интервал (np-3 , np+3 ), в который с практической достоверностью попадает количество наступлений событий при испытаниях по схеме Бернулли. Найдем этот интервал

> restart:Digits:=4:n:=10000:q:=1-p:p:=0.5:sigma:=sqrt(n*p*q);k[1]:=n*p-3*sigma;k[2]:=n*p+3*sigma;

Число 5400 не попадает в интервал от 4850 до 5150. Поэтому можно заключить, что монета несимметрична.

Пример 3. (Геометрическое распределение.). Стрелок стреляет в цель до тех пор, пока не поразит ее. Вероятность попадания при отдельном выстреле равна p, результаты выстрелов можно считать независимыми. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение числа выстрелов n.

Решение. Наложим следующие очевидные ограничения на вероятность p:

> assume(p<=1);

> additionally(p>=0);

Вероятность попадания в цель при n выстрелах ( n-1 промах и одно попадание) равна

> p[n]:=p*(1-p)^(n-1);

Найдем математическое ожидание

> nu[1]:=sum(p[n]*n, n=1..infinity);

Упростим последнее выражение

> nu[1]:=simplify(nu[1]);

Вычислим дисперсию

> mu[2]:=sum(p[n]*n^2,n=1..infinity)-nu[1]^2;

Упростим

> mu[2]:=simplify(mu[2]);

Найдем среднее квадратическое отклонение

> sigma:=sqrt(mu[2]);

Задача 2. Дискретная случайная величина имеет распределение Пуассона:

, m=0, 1, 2,...

Найти: а) математическое ожидание и дисперсию ; б) коэффициент ассиметрии .

Пример 4. Задан отрезок [a,b]. Плотность вероятности случайной величины равна (равномерное распределение).

> f(x):=piecewise(x<a,0,x>=a and x<=b,1/(b-a),x>b,0);

а) Построить функцию распределения F(x) и начертить ее график; б) найти математическое ожидание, дисперсию и среднее квадратическое отклонение величины .

Наложим условие на a и b

> assume(a<b);

Построим функцию распределения

> F(x):=piecewise(x<a,0,x>=a and x<=b,(x-a)/(b-a),x>b,1);

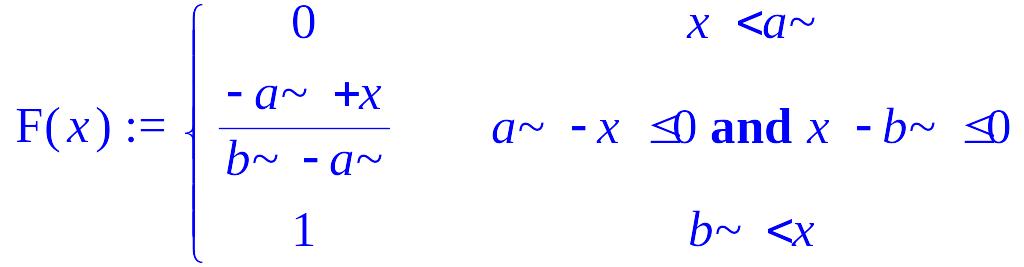
Вычислим математическое ожидание :

> nu[1]:=simplify(int(x/(b-a),x=a..b));

Найдем дисперсию

> mu[2]:=int(x^2/(b-a),x=a..b)-nu[1]^2;

Преобразуем дисперсию

> mu[2]:=factor(mu[2]);

Найдем среднее квадратическое отклонение

> sigma:=sqrt(mu[2]);

Для построения графика функции распределения параметрам a и b присвоим некоторые значения, например a=1, b=4

> a:=1:b:=4:F(x):=piecewise(x<a,0,x>=a and x<=b,(x-a)/(b-a),x>b,1):plot(F(x),x);

Задача 3. Случайная величина имеет плотность вероятности

>f(x):=piecewise(abs(x)<=Pi/2,2/Pi*(cos(x))^2,abs(x)>Pi/2,0);

Найти математическое ожидание и дисперсию .

Задача 4. Случайная величина имеет плотность вероятности (показательное распределение).

> assume(lambda>=0):f(t):=piecewise(t<0,0,t>=0,lambda*exp(-lambda*t));

а) Построить функцию распределения F(t); б) найти и ; в) найти вероятность того, что случайная величина примет значение, меньшее, чем ее математическое ожидание; г) найти вероятность

Задача 5. Случайная величина имеет плотность вероятности (нормальное распределение).

> f(x):=1/(sigma*sqrt(2*Pi))*exp(-(x-a)^2/(2*sigma^2));

Найти: а) и ; б) вероятность того, что примет значение, принадлежащее интервалу (1, 4); в) моду и медиану случайной величины .

Задача 6. Дана плотность вероятности случайной величины :

> f(x):=piecewise(x<0,0,x>=0 and x<=1,3/2*x^2,x>1 and x<=2,3/2*(2-x)^2,x>2,0);

Найти: а) начальные и центральные моменты первых четырех порядков; б) асимметрию и эксцесс этой случайной величины.

Задача 7. Коробки с шоколадом упаковываются автоматически: их средняя масса равна 1.06 кг. Найти стандартное отклонение, если 5% коробок имеют массу меньше 1 кг. Предполагается, что масса коробок распределена по нормальному закону.

Задание на практическое занятие. Внимательно ознакомьтесь с приведенными выше примерами. Решите задачи, указанные преподавателем. Сделайте выводы и оформите отчет по работе.

В отчете необходимо приводить условие решаемой задачи, излагаться ход её решения (обозначение событий, ссылки на определения и теоремы, в необходимых случаях – поясняющие рисунки, формулы, вычисления), результат и его оценка. Бумажный вариант отчета должен быть проверен и подписан студентом.